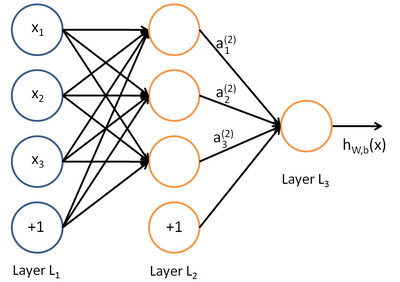
本文主要介绍多层感知器模型(MLP),它也可以看成是一种logister回归,输入层通过非线性转换,即通过隐含层把输入投影到线性可分的空间中。
如果我们在中间加一层神经元作为隐含层,则它的结构如下图所示
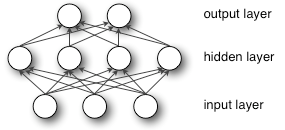
单隐层的MLP定义了一个映射:  ,其中 D和L为输入向量和输出向量f(x)的大小。
,其中 D和L为输入向量和输出向量f(x)的大小。
隐含层与输出层神经元的值通过激活函数计算出来,例如下图:如果我们选用sigmoid作为激活函数,输入设为x,要求出隐含层的激活值a,公式如下。其中 。
。
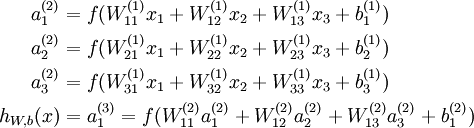
同理输出的h(x)可以用同样的公式得到,上述过程就是向前传导,因为这种联接图没有闭环或回路。
我们可以用反向传播法(backpropagation)来训练上面这个神经网络。下面主要介绍backpropation算法。
假设对于单个样例(x,y),它的代价函数(cost function)为

对于一个样本集  ,定义它的cost function为:
,定义它的cost function为:
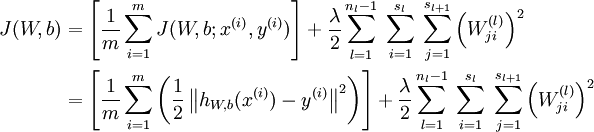
我们要做的就是最小化上述式子,类似于最小二乘,不同的是加上了第二项的权重衰减,它是用来防止过拟合,可以把它看成是一个约束项,而整个式子就是求解最值的拉格朗日公式。我们的目标是针对参数  和
和 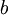 来求其函数
来求其函数  的最小值。为了求解神经网络,我们需要将每一个参数
的最小值。为了求解神经网络,我们需要将每一个参数  和
和  初始化为一个很小的、接近零的随机值(比如说,使用正态分布
初始化为一个很小的、接近零的随机值(比如说,使用正态分布  生成的随机值,其中
生成的随机值,其中 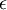 设置为
设置为 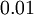 ),之后对目标函数使用诸如批量梯度下降法的最优化算法。关于w和b的初值,我根据这篇论文(Understanding the difficulty of training deep feedforward neuralnetworks)得出的结论:如果激活函数为tanh,我们设置为
),之后对目标函数使用诸如批量梯度下降法的最优化算法。关于w和b的初值,我根据这篇论文(Understanding the difficulty of training deep feedforward neuralnetworks)得出的结论:如果激活函数为tanh,我们设置为 之间的值,如果激活函数是sigmoid,则是
之间的值,如果激活函数是sigmoid,则是  。
。
关于反向传播算法的推导,UFLDL 中介绍的很清楚,我直接粘帖过来了。
既然是用梯度下降法,我们先对代价函数J求关于w和b 的偏导数,直接写出结果:

反向传播算法的思路如下:给定一个样例  ,我们首先进行"前向传导"运算,计算出网络中所有的激活值,包括
,我们首先进行"前向传导"运算,计算出网络中所有的激活值,包括  的输出值。之后,针对第
的输出值。之后,针对第 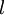 层的每一个节点
层的每一个节点 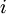 ,我们计算出其"残差"
,我们计算出其"残差" 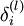 ,该残差表明了该节点对最终输出值的残差产生了多少影响。对于最终的输出节点,我们可以直接算出网络产生的激活值与实际值之间的差距,我们将这个差距定义为
,该残差表明了该节点对最终输出值的残差产生了多少影响。对于最终的输出节点,我们可以直接算出网络产生的激活值与实际值之间的差距,我们将这个差距定义为 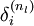 (第
(第  层表示输出层)。对于隐藏单元我们如何处理呢?我们将基于节点(译者注:第
层表示输出层)。对于隐藏单元我们如何处理呢?我们将基于节点(译者注:第 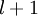 层节点)残差的加权平均值计算
层节点)残差的加权平均值计算 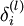 ,这些节点以
,这些节点以 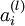 作为输入。下面将给出反向传导算法的细节:
作为输入。下面将给出反向传导算法的细节:
-
进行前馈传导计算,利用前向传导公式,得到
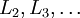 直到输出层
直到输出层 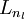 的激活值。
的激活值。 -
对于第
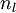 层(输出层)的每个输出单元
层(输出层)的每个输出单元 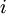 ,我们根据以下公式计算残差:
,我们根据以下公式计算残差:
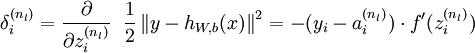
[译者注:
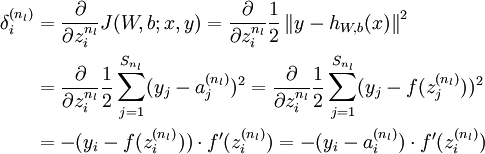
]
-
对
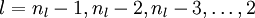 的各个层,第
的各个层,第 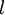 层的第
层的第 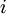 个节点的残差计算方法如下:
个节点的残差计算方法如下:
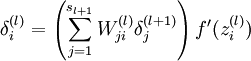
{译者注:
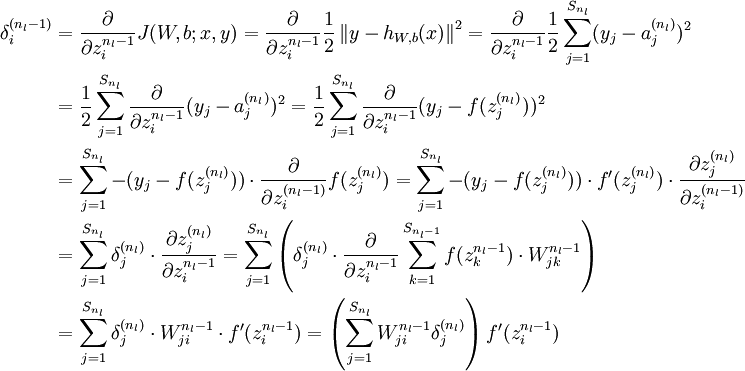
将上式中的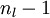 与
与 的关系替换为
的关系替换为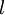 与
与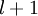 的关系,就可以得到:
的关系,就可以得到:
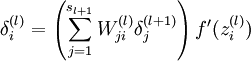
以上逐次从后向前求导的过程即为"反向传导"的本意所在。 ]
-
计算我们需要的偏导数,计算方法如下:
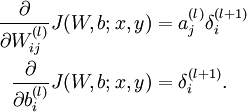
最后,我们用矩阵-向量表示法重写以上算法。我们使用" " 表示向量乘积运算符(在Matlab或Octave里用".*"表示,也称作阿达马乘积)。若
" 表示向量乘积运算符(在Matlab或Octave里用".*"表示,也称作阿达马乘积)。若  ,则
,则  。在上一个教程中我们扩展了
。在上一个教程中我们扩展了 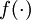 的定义,使其包含向量运算,这里我们也对偏导数
的定义,使其包含向量运算,这里我们也对偏导数 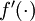 也做了同样的处理(于是又有
也做了同样的处理(于是又有 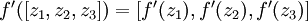 )。
)。
那么,反向传播算法可表示为以下几个步骤:
-
进行前馈传导计算,利用前向传导公式,得到
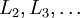 直到输出层
直到输出层 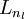 的激活值。
的激活值。 -
对输出层(第
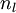 层),计算:
层),计算:
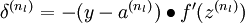
-
对于
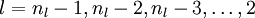 的各层,计算:
的各层,计算:
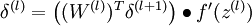
-
计算最终需要的偏导数值:
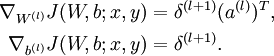
实现中应注意:在以上的第2步和第3步中,我们需要为每一个 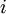 值计算其
值计算其 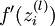 。假设
。假设 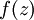 是sigmoid函数,并且我们已经在前向传导运算中得到了
是sigmoid函数,并且我们已经在前向传导运算中得到了 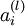 。那么,使用我们早先推导出的
。那么,使用我们早先推导出的 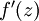 表达式,就可以计算得到
表达式,就可以计算得到 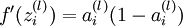 。
。
最后,我们将对梯度下降算法做个全面总结。在下面的伪代码中,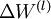 是一个与矩阵
是一个与矩阵 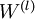 维度相同的矩阵,
维度相同的矩阵,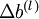 是一个与
是一个与 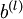 维度相同的向量。注意这里"
维度相同的向量。注意这里"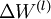 "是一个矩阵,而不是"
"是一个矩阵,而不是"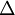 与
与  相乘"。下面,我们实现批量梯度下降法中的一次迭代:
相乘"。下面,我们实现批量梯度下降法中的一次迭代:
-
对于所有
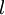 ,令
,令 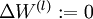 ,
, 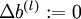 (设置为全零矩阵或全零向量)
(设置为全零矩阵或全零向量) -
对于
 到
到  ,
,-
使用反向传播算法计算
 和
和 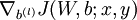 。
。 -
计算
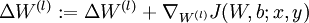 。
。 -
计算
 。
。
-
-
更新权重参数:
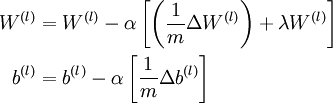
注意:为了使代价函数更快的收敛,首先要对输入数据进行归一化。
上面忘了讲tanh激活函数,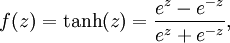 ,非线性数据围绕原点对称更容易很好的收敛代价函数,因为它们倾向于产生零均值输入到下一层,一般讲,tanh有更好的收敛性能。
,非线性数据围绕原点对称更容易很好的收敛代价函数,因为它们倾向于产生零均值输入到下一层,一般讲,tanh有更好的收敛性能。