为什么需要平滑操作
假设有一个预料集
我 喜欢 喝 奶茶
我 喜欢 吃 巧克力
我 喜欢 健身
天啦撸,一起同过窗 要出 第三季 了
这个时候要计算“我喜欢喝咖啡”的概率
假设我们用bi-gram模型来计算,也就是说
P(我喜欢喝咖啡) = P(我)P(喜欢|我)P(喝|喜欢)P(咖啡|喝) = (3/16) * (1) * (1/3) * (0) = 0
但是我们都容易感觉出来,“我喜欢喝咖啡”是符合语言习惯的句子,也就是说,虽然现在的语料库中没有这个句子,但是将来也有可能出现,但是我们算出的这个句子出现的概率是0,这不符合常识。因为语料库中没有出现“喝”后面接“咖啡”,只能说明这个句子未来出现的概率比较小,但是不排除它会出现,毕竟“我喜欢喝”这个前缀的概率该是很大的,“喝 咖啡”没有出现,只能说明“喝”后面接“咖啡”的概率很小,但是就将这个句子的概率定为0是不科学的。那么,该如何做才能使得没出现的搭配也能有一个小的概率呢?
Add-one smoothing
直接给公式:
$$P(w _{i}| w_{i-1}) = frac{C(w_{i-1}, w_{i}) + 1}{C(w_{i-1})+v} $$
这里的v是词典库的大小,注意,是词典库的大小,不是训练的预料集分词之后的词语个数。例如,对于上面那个预料集,分词之后有16个单词,但是词典库的大小是12个。所以v是12哦。
分母加1可以理解,为了让那些出现频次为0的$C(w_{i-1}, w_{i})$算出来的概率不为0,从而避免了因为它使得整个句子的概率为0了。
可是为什么分子要加v呢,笨蛋,为了使得$sum_{w_{i}}^{} frac{C(w_{i-1}, w_{i}) + 1}{C(w_{i-1})+v} $为1啊,物理意义就是,词典库中有v个词汇,$w_{i-1}$后面接的单词在这v个词汇之中的概率要为1,也就是加起来为1。
add-k Smoothing
没啥好说的,上公式:
$$P(w _{i}| w_{i-1}) = frac{C(w_{i-1}, w_{i}) + k}{C(w_{i-1})+kv} $$
只是由加1变成了加k而已啦。add-one smoothing和add-k smoothing都是拉普拉斯平滑
interpolation
但是其实上面介绍的两个平滑还是会有一个问题没有解决
下面举一个例子
假设我们有语料库
in the bathroom
the kitchen
kithcen
arboretum
如果通过add-one smoothing,我们计算P(kitchen|in the)和P(arboretum|in the)的值是一样的,因为他们的频次都是0,所以值都是(0+1)/(1+ 7) = 1/8。但是我们直观感觉,in the kitchen 肯定要比in the arboretum的概率要大得多,那么这种感觉是怎么来的呢?因为kitchen和the kitchen出现的次数大于arboretum和the arboretum啊笨蛋。所以我们计算tri-gram模型的概率的时候,如果能够考虑bi-gram和unigram的概率,那么就能避免上述情况了。
公式也很简单,如下:
$$P^{'} (w_{n}|w_{n-1},w_{n-2}) = lambda _{1}P (w_{n}|w_{n-1},w_{n-2}) +lambda _{2}P (w_{n}|w_{n-1})+lambda _{3}P (w_{n})$$
其中$lambda _{1},lambda _{2},lambda _{3}$是可以变化的参数,且满足$lambda _{1} + lambda _{2} + lambda _{3} = 1$
good-turning smoothing
老规矩,先说为什么需要发明这个算法,请看下图哦

Q1:总共18条鱼,有一条鲨鱼,好简单,不就是1/18吗
Q2:对哈,还有可能出现新鱼种,但是这个该怎么算呢,又不知道新鱼种的比例之类的,没关系,对于前面18个已经钓到的鱼来说,鲨鱼,草鱼,鳗鱼都只是钓到了一次,所以是不是可以认为是新鱼种呢,所以概率就是1/6
Q3:咦,既然新鱼种也占了一部分,那确实不能再用1/18表示接下来钓到鲨鱼的概率了呢,那么怎么表示呢,就是如下的公式:
如果对一个语料库进行统计之后,要预测接下来出现某个单词的概率
对于没有出现的单词:
$$P = frac{N_1}{N} $$
对于出现c次的单词:
$$P = frac{(c+1)N_{C+1}}{N_C*N} $$
这里的$N_c$指的是在预料集中出现频次为c的单词的个数
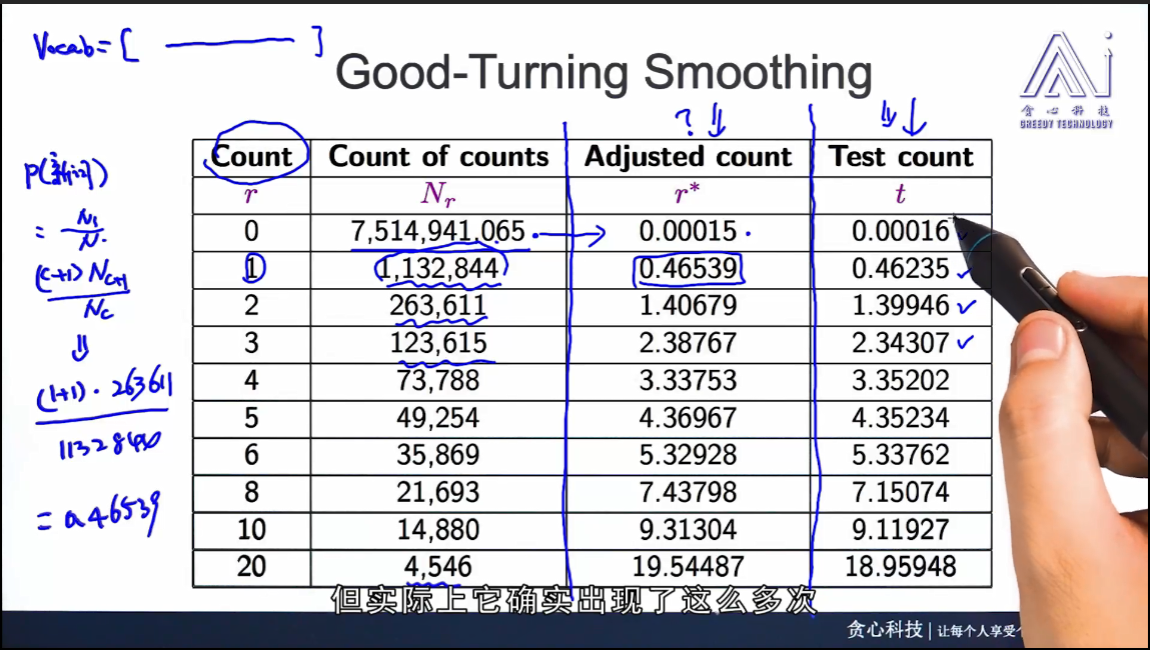
实践证明,good-turning算法得出的概率和实际情况很符合,如下图所示:第一列r是出现频次,第二列Nr是相应频次的单词个数,第三列是根据good-turning算法算出的下一次会出现的概率,第四列是在测试集中对相应频次的单词的个数的统计结果,与第三列很相似啊,兄嘚!!!!太激动了,仿佛是我发的论文一样。靠,原来不是我发的