结对开发之《返回一个二维整数数组中最大子数组的和》

一、题目要求

题目:返回一个二维整数数组中最大子数组的和。

要求： 输入一个二维整形数组，数组里有正数也有负数。 二维数组中连续的一个子矩阵组成一个子数组，每个子数组都有一个和。 求所有子数组的和的最大值。要求时间复杂度为O(n)。

结对编程要求： 两人结对完成编程任务。 一人主要负责程序分析，代码编程。 一人负责代码复审和代码测试计划。发表一篇博客文章讲述两人合作中的过程、体会以及如何解决冲突(附结对开发的工作照)。（截止到周四4月9日24:00）

二、编程思路

我们的思路比较简单，采用的是将子矩阵的和全部求出然后比较选出最大值的思路。大体思路确定了，主要就是如何求出以及怎样求出每个子矩阵的和。由于过程比较麻烦，以图片示意：

三、程序代码

#include<iostream>
#include<time.h>
using namespace std;
#define m 3  //m行数
#define n 3  //n列数

void main()
{
	int a[m][n],i,j,b[50];

	srand((int)time(0));

	//数组的值随机产生
	for(i=0;i<m;i++)
	{
		for(j=0;j<n;j++)
		{
			a[i][j]=-rand()%36+25;
		}
	}	
	
	//显示数组
	cout<<"矩阵如下："<<endl;
	for(i=0;i<m;i++)
	{
		for(j=0;j<n;j++)
		{
			cout<<a[i][j]<<'	';
		}
		cout<<endl;
	}

	int c=0,d,e,f,sum=0,sum1=0;

	//计算所有子矩阵的值
	for(i=0;i<m;i++)
	{  
		for(f=0;f<n;f++)
		{
			sum=0;
			sum1=0;
		    for(j=f;j<n;j++)
		    {
				sum+=a[i][j];
				b[c]=sum;
				c++;

				sum1=sum;
				for(d=i+1;d<m;d++)
				{
					for(e=f;e<=j;e++)
					{
						sum1+=a[d][e];
					}
					b[c]=sum1;
					c++;
				}
			}
		}
	}

	int max;
	max=b[0];
	for(i=0;i<c;i++)
	{
		if(b[i]>max)
		{
			max=b[i];
		}
	}

	cout<<"该矩阵最大子矩阵的值为："<<max<<endl;
}

　　

四、运行结果截图

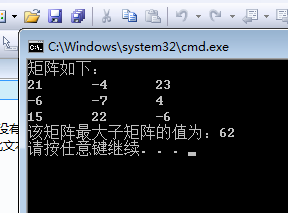
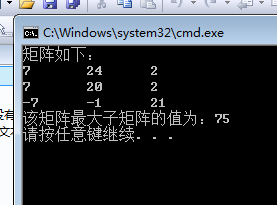
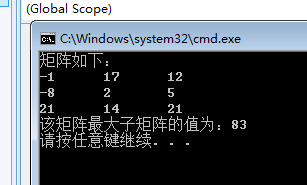
五、工作照

六、总结

此次合作主要为陈小倩同学写代码我负责程序后期的复审与测试。设计思路是两个人共同讨论出来的。两个人合作确实要比一个人的效率更高，同时思路也开阔了许多，也更容易发现平时自己一个人不容易发现的问题。通过合作我发现陈小倩同学的程序设计，写代码的思路与我都有很大不同，这也为我打开了另一个新思路。两个人再一次合作能够相互取长补短是一件好事，但是就像老师说的需要经常互换角色，因为在不同的人角色不同他的想法也不一样，最后得出的结果也一定大不相同。此次合作唯一的遗憾就是没有将时间复杂度调整到O(n),我们会再接再厉。