在打CF的时候没想到www这个dp真的蛮巧妙的
这是一道dp题(废话
假设我们走到了((i,j))位置,因为我们只能下移/右移,那么我们所有上方与左方的石块(即({ (i,j)|i<n space || space j<m })的石块)不管被推到那里都与我无瓜(可以画几张图略推一推,还是比较明显),即该题无后效性,可用dp求解。
合在一起不是很好算,我们可以考虑将右移与下移分开对其进行dp。
因此我们可以用数组(rs,ds)来记录某位置右边的石头数量以及下方的石头数量,因为只有这些石头对((i,j))的状态转移有关
设二维状态数组(r,d),表示在((i,j))位置时下一步向右((r))或向下((d))走,到达目标位置((n,m))的方案总数,由定义可得(r[n][m]=d[n][m]=1)。
重点来惹w:状态转移方程
之所以说这道题巧妙,一是因为它分成了(r,d)两块来dp,再一个就是状态转移方程了。
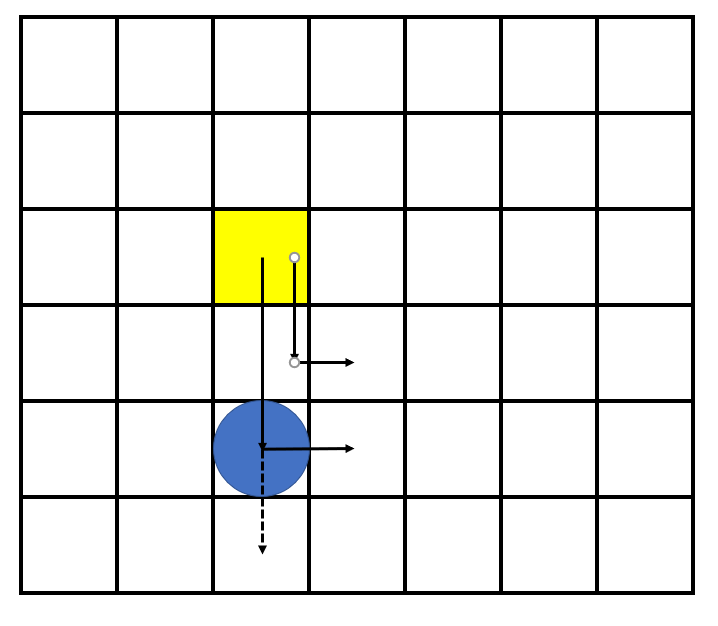
如上图所示,假设我们在黄色格子((i,j)),蓝色圆形为石头,虚线为石头移动轨迹。那么易得(ds[i][j]=1)((rs)定义忘了的看上文)。因为我们下一步必须向下走,所以我们可以选择连续走(1)步、(2)步、...一直到(n-i-ds[i][j])步为止,此时下面的石头刚好全部被一个接一个地推到了墙上排好。因此状态转移方程即
[d[i][j]=sum_{k=1}^{n-i-ds[i][j]}r[i][j+k]
]
[r[i][j]=sum_{k=1}^{m-i-rs[i][j]}d[i+k][j]
]
(提前解一个疑:这里对(r)数组进行求和而非(d)数组求和的原因是我们连续往下走了(k)步后下一步应该往右,因此这里用(r),反之亦然)
想想还是蛮巧的(或者是窝太弱啦qaq
当然一个一个枚举(r[i][j+k],d[i+k][j])肯定会超时,因此这里我们使用前缀和保存。
注意:代码里的 (ds,rs) 及 (sumd,sumr) 意义都搞反了( 感谢:@11eyes
code:
#include<bits/stdc++.h>
using namespace std;
long long n , m , r[2100][2100] , d[2100][2100] , ds[2100][2100] , rs[2100][2100];
long long sumr[2100][2100] , sumd[2100][2100];
const int mod = 1e9 + 7;
char s[2100];
//d:down r:right (update:反了
int main()
{
scanf("%d%d" , &n , &m);
for(register int i = 1 ; i <= n ; i++ )
{
scanf("%s" , s + 1);
for(register int j = 1 ; j <= m ; j++ )
{
if(s[j] == 'R') rs[i][j] = 1 , ds[i][j] = 1;
}
}
if(n == 1 && m == 1)
{
cout << (rs[1][1] ^ 1);
return 0;
}
for(register int i = n ; i >= 1 ; i-- )
{
for(register int j = m ; j >= 1 ; j-- )
{
ds[i][j] += ds[i][j + 1];
rs[i][j] += rs[i + 1][j];
}
}
r[n][m] = d[n][m] = sumd[n][m] = sumr[n][m] = 1;
for(register int i = n ; i >= 1 ; i-- )
{
for(register int j = m ; j >= 1 ; j-- )
{
if(i == n && j == m) continue;
r[i][j] = (sumd[i][j + 1] - sumd[i][m - ds[i][j + 1] + 1]) % mod;
d[i][j] = (sumr[i + 1][j] - sumr[n - rs[i + 1][j] + 1][j]) % mod;
sumr[i][j] = (sumr[i + 1][j] + r[i][j]) % mod;
sumd[i][j] = (sumd[i][j + 1] + d[i][j]) % mod;
}
}
/*for(register int i = 1 ; i <= n ; i++ )
{
for(register int j = 1 ; j <= m ; j++ )
{
cout << d[i][j] << ' ';
}
cout << endl;
}
cout << endl;
for(register int i = 1 ; i <= n ; i++ )
{
for(register int j = 1 ; j <= m ; j++ )
{
cout << r[i][j] << ' ';
}
cout << endl;
}*/
// cerr << r[1][1] << " " << d[1][1] << endl;
cout << ((r[1][1] + d[1][1]) % mod + mod) % mod;
return 0;
}