- Normal Map中的值 -
有没有想过,Normal Map(法线贴图)为什么看上去都是“偏蓝色”的?这是因为,在map中存储的值都是在Tangent Space(切空间)下的。比如,一根正好垂直于表面的法线向量在切空间下是(0,0,1),假如用一个char(注意不是unsigned char)来表达像素的话,该向量就会被转换为(0,0,127)。这样的值无疑是“蓝色”。由于大部分的法线都不会偏移这根“标准法线”太远(比如[0.1, 0.2, 0.8]...)所以大部分像素都是“偏蓝”的。用这种方式存储Normal,可以视为这种法线总是“贴着”模型表面“插”上去的,而不用考虑这根法线到底在世界空间/模型空间的什么地方,又会经过怎么样的转换。这样就可以与各种可能的空间变换操作解耦,而且直观友好,简单易懂。

- Tangent Space (切空间) -
那么,什么是切空间?我个人理解,切空间就是针对表面上某个考察的点,以该点的uv二维坐标系表达该点的切线(tangent)和该点的次法线(binormal)所构成的切平面,再加上垂直于它们的法线,就组成了一个可以用来被描述的空间。该空间就是切空间,它的坐标系(三根轴,三个基“basis”)分别是tangent(对应x), binormal(对应y)和normal(对应z)。
这里,比较难理解的是切空间和uv坐标的对应关系。不妨假想现在有一个构造非常复杂的模型,但它的表面(surface)可以像剥鹿皮一样完整剥开,而它的uv也恰可以以这样的“比喻”展开。它的法线既处处都垂直于它的表面。现在想象所有的法线都“扎”在这个表面上,然后让我们把这个表面以展uv的方式剥开并摊平(那么你现在面对的其实是一张uv set)。当你聚焦(focus)到某一个点的法线上时,这根法线正对着你,它的方向就是切空间的z轴。而这张uv set就是“切平面”。连接该点与下一点的坐标u的方向就是该点的切平面的x轴,而连接该点与下一点的坐标v的方向,就是它的切平面的y轴。
出于省事的说法,有的人可能会这样描述,“切空间下的x轴和y轴就是顶点u,v的坐标” 。如果你听到某人这么说,你可以揣测他可能是真的是行家,因为这个意思算是“点”对了。但不幸的是,严格来说,这种说法是错误的。切空间下的x轴方向(切线方向),是该点u坐标指向下一点u坐标的方向;对应地,y轴方向(次法线方向),是该点v坐标指向下一点v坐标的方向。如果你在一张uv set上审视它,也就等于是在一个二维笛卡尔坐标系上审视它,那么得到的x轴方向就是“水平”的,而y轴方向就是“竖直”的。这里想要强调的意思是,无论是切线方向还是次法线方向,它们作为一个方向,势必是由两点之间的走向关系决定的。单独的某点u,v坐标,仅仅是个值而已,单凭一个点的值,既不可能得到切线方向,也不可能得到次法线方向。换成这种说法 “切空间下的x轴和y轴就是顶点所在uv坐标系下的u轴和v轴”, 就对了。
- 求算 Tangent 与 Binormal -
- “切空间”下的切线
再来考虑一个问题。在空间中某点的position和normal是很容易知道的,那么相应也很容易得到该点的“切平面”。那么,能否随意在这个“切平面”上指定一条tangent和一条binormal,作为该点的切线和次法线?从数学理论上来讲这没问题。随着随意构造的tangent,binormal和normal指定好后,一个空间坐标系就由此指定了。当然了,根据之前的假设,这个坐标系未必是正交的(因为tangent不一定垂直于binormal),但normal = tangent cross binormal。这样的空间坐标系可以构造出无数个来,但如果要构造出上一节讨论过的“切空间”坐标系,却只能有一种构造方法。而“切空间”在行业中是一种普遍承认和使用的空间,因此有必要弄清楚如何求算这个属于“切空间”下的tangent和binormal向量。(至于将切空间和uv坐标系联系起来究竟有什么好处,我还不是太理解。暂时作为事实接受下来)。注意这里说求算tangent和binormal向量,是指它们从切空间(tangent space)被“转换”,或者说“映射(mapping)”到物体坐标系下(object space)下的值。
- 从另一个角度看“转换(映射)”
在开始正式推导前,为了能够使接下来的一个结论看起来“显而易见”,我想举一个直观的例子,从另外一个角度谈谈我对“转换”,或者说“映射”的认识。想象有一段路面在某点开始分了叉,一条路是上坡,而另一条路是下坡。一辆汽车行驶在这段路面上并开始上坡,太阳在它身后,将它的影子"映"在了那段下坡的路上。现在,可以这么理解,汽车和汽车影子分别处于不同的两个空间内,一个是上坡的空间,另一个是下坡的空间。但它们之间有某种联系,那就是当汽车在行驶时,它们都会发生相关联的变化。假如我知道,当汽车在上坡的空间中处于某点p1时,它的阴影处于下坡空间中的某点s1;当汽车前进到上坡空间中的某点p2时,它的阴影对应地前进到下坡空间中的s2。接下来我想知道,当汽车阴影在下坡的空间中前进了一个单位的长度时,对应地汽车在上坡的空间中前进了多少?
这个问题应该是“显而易见”的,答案是(p2-p1)/(s2-s1),这也是“除法”的基本含义。同时,当p2无限接近p1(由于关联性s2也无限接近s1)时,这也变成了“导数”的含义(dp/ds),因为这个问题实质上就是在问“变化率”的问题。在这个例子中,由于上坡和下坡都是一条直线,所以情况可以简化为dp = p2-p1, ds = s2-s1, 于是答案也等于dp/ds。
dp/ds这个值的单位,是处于dp所在的空间中的。回到上面这个例子中来,dp/ds这个表达式,是在说当汽车影子在自己的空间中变化ds个单位时,对应汽车在自己的空间中变化了dp个单位。同时也可以这么理解,汽车影子在自己空间中运动了ds个单位,“映射”到汽车所在的空间,汽车对应在自己的空间中运动了dp个单位。
这个问题可以概括为,自变量(x)在自己的空间内变化一个单位,“映射"到因变量(y)所在空间中,因变量会变化dy/dx个单位。
有了这个基础的理解,可以将其推广到多维的情况。自变量和因变量都处于各自的空间中,它们的维数还不一定相等。例如,考察一架飞机在单位时间(t)内位移(s)的变化,就是ds/dt。其中ds是在三维空间中,而dt却处于一维空间(时间)中。这里它们各自是几维是不重要的,关键在于自变量与因变量之间的”关联“。正是由于这种”关联“,使得当自变量只变化微小的一丁点时,因变量也会变化那么微小的一丁点。
- 向量分解 ,偏导数与 tangent = dp/du( binormal = dp/dv)
接下来,让我们回到最初的问题,如何求切空间中的”切线“对应在物体空间中的值。从上一节的讨论中,我们可以把uv空间简单看作为切空间。现在假设顶点v1的uv坐标uv1是(u1,v1),空间位置坐标是pos1是(x1,y1,z1);顶点v2的uv坐标uv2是(u2,v2),空间位置坐标pos2是(x2,y2,z2)。uv空间中v1到v2构成的二维向量为uv21 =(u2-u1, v2-v1),物体空间中v1到v2构成的三维向量为pos21 =(x2-x1, y2-y1, z2-z1)。
向量uv21实际上可以分解为两个向量,一个是与u轴平行的向量u21 = (u2-u1, 0),另一个是与v轴平行的向量v21 = (0, v2-v1)。 由向量分解定理可知uv21 = u21 + v21。实际上,我们可以在uv空间中找到一点uv^ = (u2, v1),使得uv^ - uv1 = u21,uv2 - uv^ = v21。由于u轴在切空间中就是切线的方向,因此u21平行于切线;同理v21平行于次法线。
既然uv空间中存在一点uv^,那么”映射“到物体空间中,也会对应存在一点pos^。使得pos21 = (pos^-pos1) + (pos2 - pos^)。这个向量分解的动作和上面uv空间中的向量分解是对应的。只是我们还不知道这个pos^到底处于物体空间中的哪个位置。但是,我们知道,当点在uv空间中从uv1变化到uv^时,对应地顶点在物体空间中则从pos1变化到了pos^。这是多么熟悉的句式!进而我们假设,如果点在uv空间中沿着uv1->uv^的方向变化一个单位时,”映射“到物体空间中顶点会沿着pos1->pos^的方向变化多少呢?答案就是(pos^-pos1)/(uv^-uv1) == (pos^-pos1)/u21 == dp/du。由于du在uv空间(也就是切空间)中的方向与切线相同,因此dp就是对应在物体空间中切线的方向。dp/du是单位化的值,我们就可以将其看作是物体空间中的切线向量。于是得到tangent = dp/du。
同理可以得到binormal = dp/dv。
实际上,由于u21对pos2-pos1的影响已经被分解到了(pos^-pos1)上, u21的v轴分部对其不产生任何影响,所以这里简单令u21 = u2-u1(注意这里没加粗体,表示它是标量)。可以得到dp/du = (pos^-pos1)/u21。同理有 dp/dv = (pos2-pos^)/v21(v21 = v2 - v1)。这实际上就是”偏导数“(partial derivative)的含义。
总结一下上面的分析,我们可以推导出下面的结论:
已知 u21 = u2-u1 和 v21 = v2-v1,
则有 dp/du = (pos^-pos1)/u21 , dp/dv = (pos2-pos^)/v21,
得到 (pos^-pos1) = dp/du * u21, (pos2-pos^) = dp/dv * v21
于是 pos21 = (pos^-pos1) + (pos2 - pos^) = (dp/du) * u21 + (dp/dv) * v21
等同于 pos2 - pos1 = (dp/du) * (u2-u1) + (dp/dv) * (v2-v1)
- *扩展阅读 : pbrt中的 pi = p0 + (dp/du) * u + (dp/dv) * v
(注:如果你没在看《pbrt》,或者你从没见过上面这个公式,那么此节可以略过不看。这节只是源于自问自答的一个想法。曾经为理解这个公式卡了很久,既然现在稍稍有些心得,那也该本着有始有终的态度全部记录下来为好。)
读过pbrt的同学知道,第3.6.2节讲的是如何求得射线与三角形相交的那一点“微面(facet)"的全部信息。其中就包括tangent和binormal。只不过,它将tangent值表达成了dp/du, binormal值表达成了dp/dv。关于这个观点,在本文的上一节中已经进行了力所能及的理解。只不过,书中在进行推导时,是从下面这个假设起步的,即在由三个点pi(i=1,2,3)组成的三角形中,设p0是三角形所在平面的其中一点,那么则有:pi = p0 + (dp/du) * u + (dp/dv) * v。
这里,我就想补充解释一下为什么会有这个结论。
说起来也简单,只是书中没有明说,这个p0点对应的uv坐标值就是(0,0)。然后我们把这个公式变通一下,就成了:pi - p0 = (dp/du)*(u-0) + (dp/dv)*(v-0)。这个公式,就很像本文上节最后得到的结论。只不过是把点2换成了点i,点1换成了点0。书中的意思是说,在这个三角形所在的这个平面上,任意一点都可以通过这种公式计算得到,只要给定了uv(0,0)对应的p0点以及欲求点的uv坐标值(u,v)即可。
这里可能让人感到困惑的一个地方是,uv坐标与顶点之间的对应关系,一般是通过人为指定的。那凭什么认为uv坐标基点(0,0)所对应的p0,会恰好在pi(i=1,2,3)这个三角形所在的平面上?实际上这里说的uv坐标(0,0)点,并不是我们通常认为的人为指定的那个点,而是从数学角度上”推断“出的一个点。可以这样理解。既然我们知道三角形的三个顶点的三维空间坐标值(xi, yi, zi)(i=1,2,3)与uv坐标值(ui, vi)(i=1,2,3),又知道三点能够确定一个平面这个常识。那么就可以推断出在uv空间中的任意一点,在三角形所在的这个平面中必定存在对应的顶点。 那么也就可以确定在这个平面上找到一点p0,使得它的uv坐标值是(0,0)。
- 开始求算!
有了以上知识理解上的准备,接下来的求算任务基本上就是直截了当的了,没什么太需要费脑力的地方。不过需要对线性代数的基础知识有点了解: 其实只要知道如何求逆矩阵就行了。
切线和次法线永远总是针对面(face)而言的,单独考察一个点的切线或是次法线没有意义。而构成一个面最简单的方式就是三角形,所以我们就考察如何求算三角形的tangent和binormal。给定一个三角形,已知它的三个物理空间的顶点为pi(i=1,2,3),对应的uv空间坐标为uvi(i=1,2,3)。由于这是一个三角形平面,因此三个点的tangent值与binormal值都是该面上的值。设 tangent = dp/du, binormal = dp/dv。根据上几节的推导,我们很容易就可以得到,
p2 - p1 = dp/du * (u2 - u1) + dp/dv * (v2 - v1)
p3 - p1 = dp/du * (u3 - u1) + dp/dv * (v3 - v1)
修改成矩阵形式,就成了下面这样,
再变换一下,就得到
求解这个式子的细节就不列在这里了。关键了解一下如何求一个矩阵的逆矩阵(伴随矩阵数除其行列式),然后根据矩阵的乘法运算规则就能得到结果。随着结果的求得,我们也就知道了tangent和binormal的值。
- TBN Matrix (TBN 矩阵)
上节求得了tangent(简写为T)与binormal(简写为B),再叉乘一下就得到了normal(简写为N):即 N = T X B。 由此三个向量就可以构成一个空间,[T, B, N]。
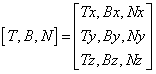
这个矩阵表示的是,切空间(tangent space)中的三个基向量被转换到当前坐标系下所对应的三个基向量构成的空间。任何一个切空间下的向量,通过这个矩阵便可以变换到当前坐标系下(比如模型的物体坐标系亦或它所在的世界坐标系),究竟被转到什么坐标系,这要看当时求算T,B时利用的Pi点所在的空间:如果Pi是模型的物体坐标系,那对应该矩阵也就会把切空间的向量转到物体坐标系下;如果Pi是模型所在的世界坐标系,那对应矩阵就会把向量转到世界坐标系下。比如,
normal in object space = [T,B,N] X normal in tangent space
这里我们关心的问题是,这种转换的意义是什么?费这么大劲做转换,到底是为了什么?答案是,通过这种转换,就可以把Normal Map中的法线转换到对应的物体/世界坐标系下,与这个空间下的光线进行计算,从而能够算出对应此点的正确光照。我们知道Normal Map的法线为什么存储在“切空间”下是有道理的(第一节有提到),但它不能直接被使用。经过这样的转换,就可以与各种可能的空间坐标联系起来了。
不过经常用的,还不是把normal值转换到物体/世界坐标系下,而是反过来,把光线“反”转换到到切空间下,与normal计算出光照值。为什么?因为一个模型可能有非常多的点,对应normal map中的normal值数量必然也是巨大的,如果把每一根normal都做转换,这种计算量的成本是相当高的。但反过来,光线就那么几条,转换一次光线就能给所有切空间下的normal使用,相对来说这种计算要“便宜”得多,所以反转光线值这种做法是更为常见的做法。
light in tangent space = [T,B,N]-1 X light in object space
同样需要求其逆矩阵。不过如果TBN三向量彼此正交的话(一般来说是这样),那么它的逆矩阵就简单地等于它的转置矩阵。
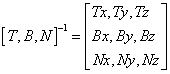
实际上TBN的作用还不止于此,它的应用很广泛而且也非常重要。比如做displacement mapping时,基于Vector置换的做法就同样用到了TBN矩阵。用法和原理与Normal Map都是一样的,只不过此时Map换成了再切空间下的用来置换的向量,而非法线。
-----------------------
reference :
3.book "pbrt"(2nd edition) section-3.6.2