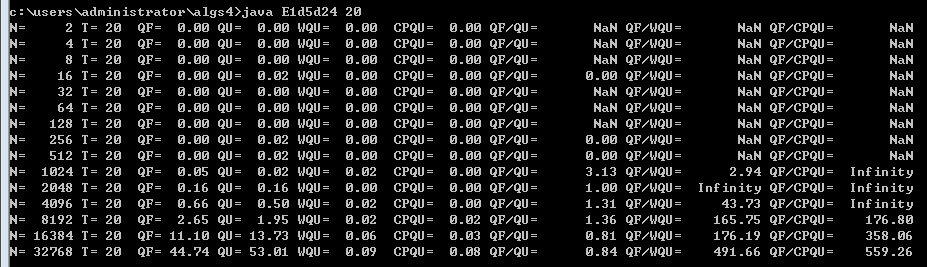
1.5.24适用于Erdos-Renyi模型的快速算法。在练习1.5.23的测试中增加加权quick-union算法和使用路径压缩的加权quick-union算法。你能分辨出这两种算法的区别吗?
答:加权quick-union最坏情况下树深度为lgN,N为节点数,路径压缩的加权quick-union算法最坏情况下树深度为1。
public class E1d5d24
{
public static class Connection
{
int p;
int q;
public Connection(int p,int q)
{this.p=p; this.q=q;}
public int P()
{return p;}
public int Q()
{return q;}
}
//
public static int[][] Generate(int N)
{
Queue<Connection> cnns=new Queue();
WeightedQuickUnionUF uf=new WeightedQuickUnionUF(N);
while (uf.count()>1)
{
int p=StdRandom.uniform(N);
int q=StdRandom.uniform(N);
uf.union(p,q);
cnns.enqueue(new Connection(p,q));
}//end while
//
int[][] cnnsOfArray=new int[cnns.size()][2];
int i=0;
while(!cnns.isEmpty())
{
Connection item=cnns.dequeue();
cnnsOfArray[i][0]=item.P();
cnnsOfArray[i][1]=item.Q();
i++;
}
return cnnsOfArray;
}
public static double QuickFindElapsedTime(int[][] cnns,int T,int N)
{
Stopwatch timer=new Stopwatch();
for (int t=1;t<=T;t++)
{
QuickFindUF uf=new QuickFindUF(N);
int i=0;
while(uf.count()>1)
{
uf.union(cnns[i][0],cnns[i][1]);
i++;
}
}
return timer.elapsedTime();
}
public static double QuickUnionElapsedTime(int[][] cnns,int T,int N)
{
Stopwatch timer=new Stopwatch();
for (int t=1;t<=T;t++)
{
QuickUnionUF uf=new QuickUnionUF(N);
int i=0;
while(uf.count()>1)
{
uf.union(cnns[i][0],cnns[i][1]);
i++;
}
}
return timer.elapsedTime();
}
public static double WeightedQuickUnionElapsedTime(int[][] cnns,int T,int N)
{
Stopwatch timer=new Stopwatch();
for (int t=1;t<=T;t++)
{
WeightedQuickUnionUF uf=new WeightedQuickUnionUF(N);
int i=0;
while(uf.count()>1)
{
uf.union(cnns[i][0],cnns[i][1]);
i++;
}
}
return timer.elapsedTime();
}
public static double CompressPathQuickUnionElapsedTime(int[][] cnns,int T,int N)
{
Stopwatch timer=new Stopwatch();
for (int t=1;t<=T;t++)
{
E1d5d12 uf=new E1d5d12(N);
int i=0;
while(uf.count()>1)
{
uf.union(cnns[i][0],cnns[i][1]);
i++;
}
}
return timer.elapsedTime();
}
public static void main(String[] args)
{
int T=Integer.parseInt(args[0]);
for (int N=2;N<=Math.pow(2,15);N=N+N)
{
int[][] cnns=Generate(N);
double QuickFindTime=QuickFindElapsedTime(cnns,T,N);
double QuickUnionTime= QuickUnionElapsedTime(cnns,T,N);
double WeightedQuickUnionTime=WeightedQuickUnionElapsedTime(cnns,T,N);
double CompressPathQuickUnionTime=CompressPathQuickUnionElapsedTime(cnns,T,N);
StdOut.printf("N=%6d T=%3d QF=%6.2f QU=%6.2f WQU=%6.2f CPQU=%6.2f QF/QU=%10.2f QF/WQU=%10.2f QF/CPQU=%10.2f ", N, T,QuickFindTime,QuickUnionTime,WeightedQuickUnionTime,CompressPathQuickUnionTime,QuickFindTime/QuickUnionTime,QuickFindTime/WeightedQuickUnionTime,QuickFindTime/CompressPathQuickUnionTime);
}
}
}
答:加权quick-union最坏情况下树深度为lgN,N为节点数,路径压缩的加权quick-union算法最坏情况下树深度为1。

public class E1d5d24
{
public static class Connection
{
int p;
int q;
public Connection(int p,int q)
{this.p=p; this.q=q;}
public int P()
{return p;}
public int Q()
{return q;}
}
//
public static int[][] Generate(int N)
{
Queue<Connection> cnns=new Queue();
WeightedQuickUnionUF uf=new WeightedQuickUnionUF(N);
while (uf.count()>1)
{
int p=StdRandom.uniform(N);
int q=StdRandom.uniform(N);
uf.union(p,q);
cnns.enqueue(new Connection(p,q));
}//end while
//
int[][] cnnsOfArray=new int[cnns.size()][2];
int i=0;
while(!cnns.isEmpty())
{
Connection item=cnns.dequeue();
cnnsOfArray[i][0]=item.P();
cnnsOfArray[i][1]=item.Q();
i++;
}
return cnnsOfArray;
}
public static double QuickFindElapsedTime(int[][] cnns,int T,int N)
{
Stopwatch timer=new Stopwatch();
for (int t=1;t<=T;t++)
{
QuickFindUF uf=new QuickFindUF(N);
int i=0;
while(uf.count()>1)
{
uf.union(cnns[i][0],cnns[i][1]);
i++;
}
}
return timer.elapsedTime();
}
public static double QuickUnionElapsedTime(int[][] cnns,int T,int N)
{
Stopwatch timer=new Stopwatch();
for (int t=1;t<=T;t++)
{
QuickUnionUF uf=new QuickUnionUF(N);
int i=0;
while(uf.count()>1)
{
uf.union(cnns[i][0],cnns[i][1]);
i++;
}
}
return timer.elapsedTime();
}
public static double WeightedQuickUnionElapsedTime(int[][] cnns,int T,int N)
{
Stopwatch timer=new Stopwatch();
for (int t=1;t<=T;t++)
{
WeightedQuickUnionUF uf=new WeightedQuickUnionUF(N);
int i=0;
while(uf.count()>1)
{
uf.union(cnns[i][0],cnns[i][1]);
i++;
}
}
return timer.elapsedTime();
}
public static double CompressPathQuickUnionElapsedTime(int[][] cnns,int T,int N)
{
Stopwatch timer=new Stopwatch();
for (int t=1;t<=T;t++)
{
E1d5d12 uf=new E1d5d12(N);
int i=0;
while(uf.count()>1)
{
uf.union(cnns[i][0],cnns[i][1]);
i++;
}
}
return timer.elapsedTime();
}
public static void main(String[] args)
{
int T=Integer.parseInt(args[0]);
for (int N=2;N<=Math.pow(2,15);N=N+N)
{
int[][] cnns=Generate(N);
double QuickFindTime=QuickFindElapsedTime(cnns,T,N);
double QuickUnionTime= QuickUnionElapsedTime(cnns,T,N);
double WeightedQuickUnionTime=WeightedQuickUnionElapsedTime(cnns,T,N);
double CompressPathQuickUnionTime=CompressPathQuickUnionElapsedTime(cnns,T,N);
StdOut.printf("N=%6d T=%3d QF=%6.2f QU=%6.2f WQU=%6.2f CPQU=%6.2f QF/QU=%10.2f QF/WQU=%10.2f QF/CPQU=%10.2f ", N, T,QuickFindTime,QuickUnionTime,WeightedQuickUnionTime,CompressPathQuickUnionTime,QuickFindTime/QuickUnionTime,QuickFindTime/WeightedQuickUnionTime,QuickFindTime/CompressPathQuickUnionTime);
}
}
}