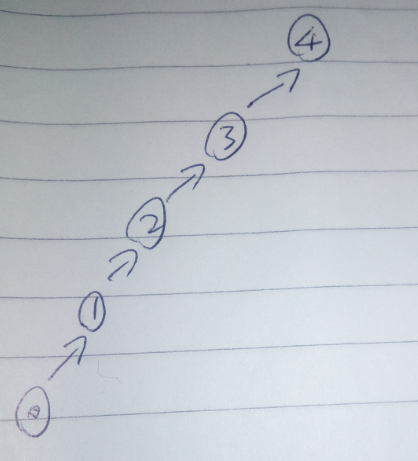
1.5.12使用路径压缩的quick-union算法。根据路径压缩修改quick-union算法(请见1.5.2.3节),在find()方法中添加一个循环来将从p到根节点的路径上的每个触点都连接到根节点。给出一列输入,使该方法能够产生一条长度为4的路径。注意:该算法的所有操作的均摊成本已知为对数级别。
答:
0-1
1-2
2-3
3-4
tinyUF.txt
5
0
1
1
2
2
3
3
4
public class E1d5d12
{
private int[] id;
private int count;
public E1d5d12(int N)
{
count=N;
id=new int[N];
for (int i=0;i<N;i++)
id[i]=i;
}
public int count()
{return count;}
boolean connected(int p,int q)
{return find(p)==find(q);}
public int find(int p)
{
int temp=p;
//find root
while(p!=id[p]) p=id[p];
int root=p;
//set all node's father is root
p=temp;
while(root!=id[p])
{
temp=id[p];
id[p]=root;
p=temp;
}
return root;
}
public void union(int p,int q)
{
int pRoot=find(p);
int qRoot=find(q);
if(pRoot==qRoot) return;
id[pRoot]=qRoot;
count--;
}
public static void main(String[] qrgs)
{
int N=StdIn.readInt();
E1d5d12 uf=new E1d5d12(N);
while (!StdIn.isEmpty())
{
int p=StdIn.readInt();
int q=StdIn.readInt();
if(uf.connected(p,q)) continue;
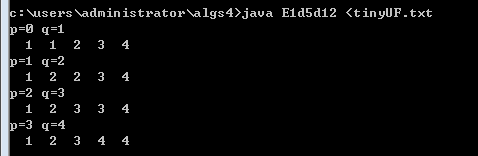
StdOut.printf("p=%d q=%d ",p,q);
uf.union(p,q);
}//end while
}//end main
}//end class
答:
0-1
1-2
2-3
3-4


tinyUF.txt
5
0
1
1
2
2
3
3
4
public class E1d5d12
{
private int[] id;
private int count;
public E1d5d12(int N)
{
count=N;
id=new int[N];
for (int i=0;i<N;i++)
id[i]=i;
}
public int count()
{return count;}
boolean connected(int p,int q)
{return find(p)==find(q);}
public int find(int p)
{
int temp=p;
//find root
while(p!=id[p]) p=id[p];
int root=p;
//set all node's father is root
p=temp;
while(root!=id[p])
{
temp=id[p];
id[p]=root;
p=temp;
}
return root;
}
public void union(int p,int q)
{
int pRoot=find(p);
int qRoot=find(q);
if(pRoot==qRoot) return;
id[pRoot]=qRoot;
count--;
}
public static void main(String[] qrgs)
{
int N=StdIn.readInt();
E1d5d12 uf=new E1d5d12(N);
while (!StdIn.isEmpty())
{
int p=StdIn.readInt();
int q=StdIn.readInt();
if(uf.connected(p,q)) continue;
StdOut.printf("p=%d q=%d ",p,q);
uf.union(p,q);
}//end while
}//end main
}//end class