ORM:对象关系映射,主要实现模型对象到关系数据库数据的映射
ORM图解:
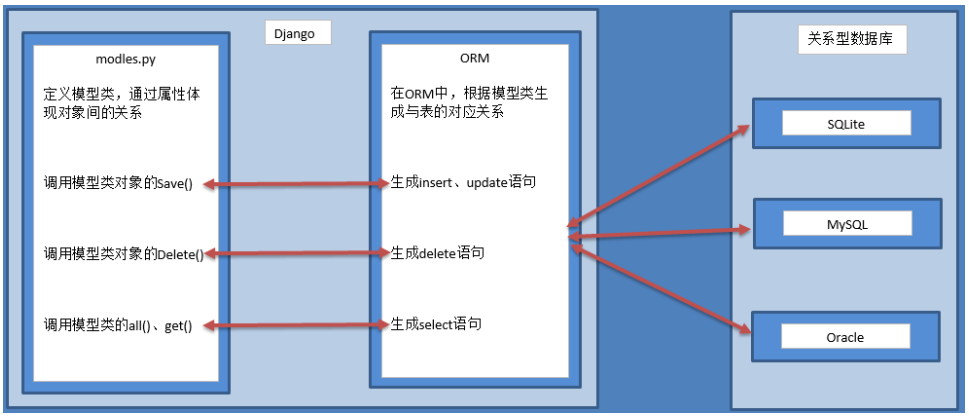
优点 :
• 只需要面向对象编程, 不需要面向数据库编写代码.
• 对数据库的操作都转化成对类属性和方法的操作.
• 不用编写各种数据库的sql语句.
• 实现了数据模型与数据库的解耦, 屏蔽了不同数据库操作上的差异.
• 不在关注用的是mysql、oracle...等.
• 通过简单的配置就可以轻松更换数据库, 而不需要修改代码.
缺点 :
• 相比较直接使用SQL语句操作数据库,有性能损失.
• 根据对象的操作转换成SQL语句,根据查询的结果转化成对象, 在映射过程中有性能损失.
一、ORM简介
对象关系映射(Object Relational Mapping,简称ORM)模式是一种为了解决面向对象与关系数据库存在的互不匹配的现象的技术。简单的说,ORM是通过使用描述对象和数据库之间映射的元数据,将程序中的对象自动持久化到关系数据库中。那么,到底如何实现持久化呢?一种简单的方案是采用硬编码方式,为每一种可能的数据库访问操作提供单独的方法。
这种方案存在以下不足:
1.持久化层缺乏弹性。一旦出现业务需求的变更,就必须修改持久化层的接口
2.持久化层同时与域模型与关系数据库模型绑定,不管域模型还是关系数据库模型发生变化,毒药修改持久化曾的相关程序代码,增加了软件的维护难度。
ORM提供了实现持久化层的另一种模式,它采用映射元数据来描述对象关系的映射,使得ORM中间件能在任何一个应用的业务逻辑层和数据库层之间充当桥梁。Java典型的ORM中间件有:Hibernate,ibatis,speedframework。
ORM的方法论基于三个核心原则:
· 简单:以最基本的形式建模数据。
· 传达性:数据库结构被任何人都能理解的语言文档化。
· 精确性:基于数据模型创建正确标准化了的结构。
二、ORM的概念
让我们从O/R开始。字母O起源于"对象"(Object),而R则来自于"关系"(Relational)。几乎所有的程序里面,都存在对象和关系数据库。在业务逻辑层和用户界面层中,我们是面向对象的。当对象信息发生变化的时候,我们需要把对象的信息保存在关系数据库中。
当你开发一个应用程序的时候(不使用O/R Mapping),你可能会写不少数据访问层的代码,用来从数据库保存,删除,读取对象信息,等等。你在DAL中写了很多的方法来读取对象数据,改变状态对象等等任务。而这些代码写起来总是重复的。
ORM解决的主要问题是对象关系的映射。域模型和关系模型分别是建立在概念模型的基础上的。域模型是面向对象的,而关系模型是面向关系的。一般情况下,一个持久化类和一个表对应,类的每个实例对应表中的一条记录,类的每个属性对应表的每个字段。
ORM技术特点:
1.提高了开发效率。由于ORM可以自动对Entity对象与数据库中的Table进行字段与属性的映射,所以我们实际可能已经不需要一个专用的、庞大的数据访问层。
2.ORM提供了对数据库的映射,不用sql直接编码,能够像操作对象一样从数据库获取数据。
三、ORM的优缺点
ORM的缺点是会牺牲程序的执行效率和会固定思维模式。
从系统结构上来看,采用ORM的系统一般都是多层系统,系统的层次多了,效率就会降低。ORM是一种完全的面向对象的做法,而面向对象的做法也会对性能产生一定的影响。
在我们开发系统时,一般都有性能问题。性能问题主要产生在算法不正确和与数据库不正确的使用上。ORM所生成的代码一般不太可能写出很高效的算法,在数据库应用上更有可能会被误用,主要体现在对持久对象的提取和和数据的加工处理上,如果用上了ORM,程序员很有可能将全部的数据提取到内存对象中,然后再进行过滤和加工处理,这样就容易产生性能问题。
在对对象做持久化时,ORM一般会持久化所有的属性,有时,这是不希望的。
但ORM是一种工具,工具确实能解决一些重复,简单的劳动。这是不可否认的。但我们不能指望工具能一劳永逸的解决所有问题,有些问题还是需要特殊处理的,但需要特殊处理的部分对绝大多数的系统,应该是很少的。