@
一、系统流程与符号说明


1、定义流形中的+-
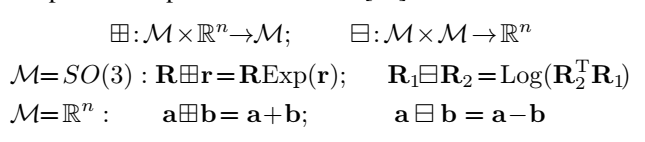
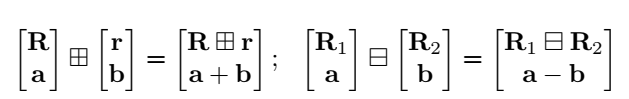
从上面的定义,很容易验证
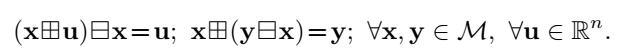
IEKF
| 符号 | 含义 |
|---|---|
| (mathbf{z}_{j}^{kappa}=mathbf{G}_{j}left({ }^{G} widehat{mathbf{p}}_{f_{j}}^{kappa}-{ }^{G} mathbf{q}_{j} ight)) | (mathbf{z}_{j}^{kappa}) LOAM的点到线、 点到面误差作为残差 |
| G() | 计算点到线、点到面残差的函数 |
| ({ }^{G} mathbf{q}_{j}) | 真值 |
| (widehat{x}) | IMU积分的当前位姿 |
| (widehat{mathbf{P}}_{k}) | IMU协方差 |
| ({ }^{L_{j}} mathbf{n}_{f_{j}}) | 雷达测量噪声 |
| ({ }^{L_{j}} mathbf{p}_{f_{j}}^{mathrm{gt}}={ }^{L_{j}} mathbf{p}_{f_{j}}-{ }^{L_{j}} mathbf{n}_{f_{j}}) | 雷达真值 = 测量值 - 噪声 |
| T | 变换矩阵 |
观察方程:
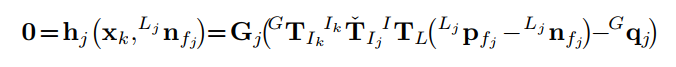
用它在(widehat{mathbf{x}}_{k}^{kappa})处的一阶近似来逼近上面的方程会得到
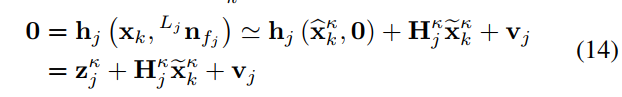
(mathbf{H}_{j}^{kappa}) 是(h_j())关于 (widetilde{mathbf{x}}_{k}^{kappa})的雅克比
(v_j) 测量噪声,这里定义为了一个白噪声
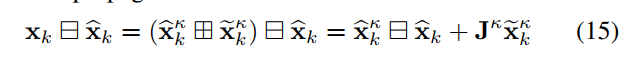
(J^k)是(left(widehat{mathbf{x}}_{k}^{kappa} mathbb{square{}} widetilde{mathbf{x}}_{k}^{kappa}
ight) square widehat{mathbf{x}}_{k}) 的雅克比
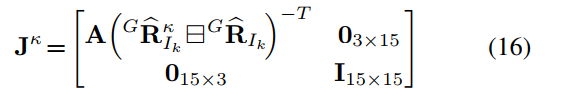
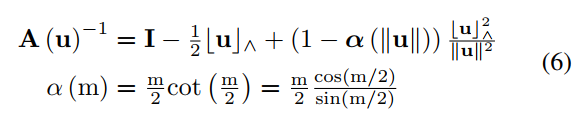
迭代初值为: (widehat{mathbf{x}}_{k}^{kappa}=widehat{mathbf{x}}_{k}), then (mathbf{J}^{kappa}=mathbf{I})
将(15)中的先验与(14)中的后验分布相结合,得到最大后验估计(MAP):
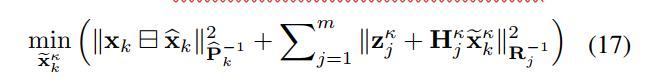
得到迭代卡尔曼公式
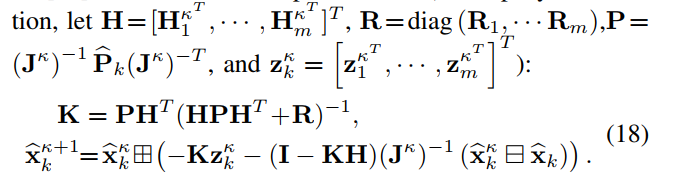
R是雷达测量噪声矩阵
重复上面的步骤直至收敛,得到
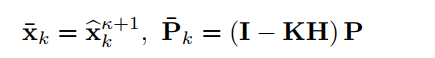
其中卡尔曼增益公式(18)可以用下面的公式替换,他们是等价的。这避免了对测量矩阵H求逆
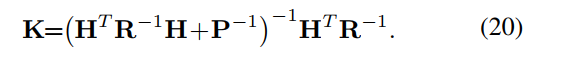
算法步骤
