用C++实现图的DFS和BFS(邻接表)
概述
图的储存方式有邻接矩阵和邻接表储存两种。由于邻接表的实现需要用到抽象数据结构里的链表,故稍微麻烦一些。C++自带的STL可以方便的实现List,使算法的实现变得简单起来
算法概述
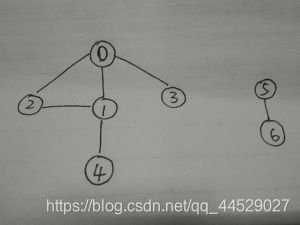
为了让我们的算法更有普适性,我们将非连通图也考虑在内。其实,要想遍历到类似于图中5,6节点这种孤岛节点,只需要依次按编号遍历顺序所有节点,如果某节点没有访问(book数组标记值为0),则从该节点开始深度优先搜索或广度优先搜索;等一次深搜或广搜完毕后,继续依次按照编号顺序遍历节点,选择从一个没访问过的结点开始再次深搜或广搜。。。如此知道把所有节点都遍历完。
代码
1.图抽象数据类型的声明,除了构造函数和析构函数之外,提供3个对外接口,分别实现递归DFS,BFS和非递归DFS(用STL栈实现)
using namespace std;
struct Graph{
//储存节点的邻接表
vector<list<int>> vertex;
//标记数组
bool book[100];
//n代表总节点个数
Graph(int n);
~Graph();
//对外接口,算法的驱动函数
void DFS_recursion_boost();
void BFS_boost();
void DFS_stack_boost();
private://内部算法实现
void DFS_recursion(int cur);
void BFS(int cur);
void DFS_stack(int cur);
};
2.图的构造函数和析构函数实现
Graph::Graph(int n){
vertex.resize(n);
for(int i=0;i<n;++i){
int adj;
cout<<"请输入"<<i<<"号节点邻接链表(以-1表示结束输入)"<<endl;
cin>>adj;
while(adj!=-1){
vertex[i].push_back(adj);
cin>>adj;
}
}
memset(book,0,sizeof(book));
}
Graph::~Graph(){
vertex.clear();
}
3.图的递归DFS调用接口及其实现函数
void Graph::DFS_recursion_boost(){
for(int i=0;i<vertex.size();++i){
DFS_recursion(i);
}
}
void Graph::DFS_recursion(int cur){
if(book[cur]==1) return;
book[cur]=1;
cout<<cur;
for(auto iter=vertex[cur].begin();iter!=vertex[cur].end();++iter){
if(book[*iter]==0){
DFS_recursion(*iter);
}
}
}
4.图的BFS调用接口及其实现函数
void Graph::BFS_boost(){
for(int i=0;i<vertex.size();++i){
BFS(i);
}
}
void Graph::BFS(int cur){
queue<int> q;
if(book[cur]==0){
q.push(cur);
}
while(!q.empty()){
int front=q.front();
q.pop();
cout<<front;
book[front]=1;
for(auto iter=vertex[front].begin();iter!=vertex[front].end();++iter){
if(book[*iter]==0){
q.push(*iter);
}
}
}
}
5.图的非递归DFS及其实现函数
void Graph::DFS_stack_boost(){
for(int i=0;i<vertex.size();++i){
DFS_stack(i);
}
}
void Graph::DFS_stack(int cur)
{
stack<int> s;
if(book[cur]==0){
s.push(cur);
}
while(!s.empty()){
int top=s.top();
if(book[top]==0){
book[top]=1;
cout<<top;
}
else{
s.pop();
// top=s.top();为何不要?
}
for(auto iter=vertex[top].begin();iter!=vertex[top].end();++iter){
if(book[*iter]==0){
s.push(*iter);
break;
}
}
}
}
6.主函数测试(注意,每次遍历后要把标记数组初始化为0)
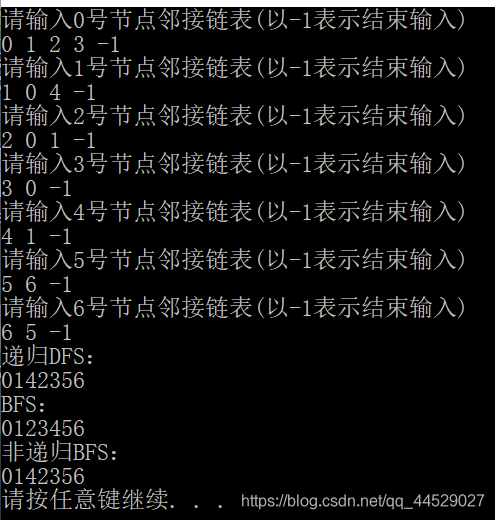
int main(){
Graph G(7);
cout<<"递归DFS:"<<endl;
G.DFS_recursion_boost();
memset(G.book,0,100);
cout<<endl;
cout<<"BFS:"<<endl;
G.BFS_boost();
memset(G.book,0,100);
cout<<endl;
cout<<"非递归BFS:"<<endl;
G.DFS_stack_boost();
memset(G.book,0,100);
cout<<endl;
system("pause");
return 0;
}
输出