2020牛客暑期多校第二场（缺EK）

题目说明：

A.All with Pairs（KMP+Hash）               B.Boundary（计算几何-三点定圆）

C.Cover the Tree（思维+dfs序）             D.Duration（签到题-模拟）

F.Fake Maxpooling（单调队列）

G.Greater and Greater（黑科技bitset）  H.Happy Triangle（动态开点线段树）

I.Interval（最小割转对偶图最短路）          J.Just Shuffle（数论置换）

A.All with Pairs

题目大意：给你n个字符串，定义$f(s,t)$为最大的$i$能够使得字符串s位于$i$的前缀和字符串t位于$|t|-i+1$的后缀相等，若不存在则$f(s,t)=0$。问题是求$sum_{i=1}^{n}sum_{j=1}^{n}f(s_i,s_j)^2%998244353$，字符串总长不超过1e6

输入

3
ab
ba
aba

输出

29

既然找的是最大的$i$那么我们可以统计每个前缀在后缀中出现的次数，然后对每个字符串的前缀找到他的次数，并删除重复的次数，这个重复的位置可以利用KMP来寻找，那么也就是说假如当前位置前缀出现在后缀中的次数为$num[j]$个，那么我们要做的就是$num[nxt[i][j]]-=num[j]$。比如说对于$aba$而言如果该前缀出现了，那么$a$前缀也会出现一次，所以就会多出来。最后将数量乘以位置的平方就好了

以下是AC代码：

#include <bits/stdc++.h>
using namespace std;
 
#define debug printf("@#$@$#@$##&*
")
const int mac=2e3+10;
const double esp=1e-9;
 
struct node
{
    double x,y;
}a[mac];
 
struct Point
{
    double x,y;
    int ok;
    bool operator <(const Point &a)const{
        if (fabs(x-a.x)<esp) return y<a.y;
        return x<a.x;
    }
};
Point OS[mac*mac];
  
Point find(node p1,node p2,node p3) {
    if(fabs((p1.x - p2.x) * (p1.y - p3.y) - (p1.x - p3.x) * (p1.y - p2.y)) <esp) {
        return Point{0,0,0};
    }
    double a1 = ((p1.x * p1.x - p2.x * p2.x) + (p1.y * p1.y - p2.y * p2.y)) / 2;
    double a2 = ((p1.x * p1.x - p3.x * p3.x) + (p1.y * p1.y - p3.y * p3.y)) / 2;
      
    Point O;
    O.x = ((p1.y - p2.y) * a2 - (p1.y - p3.y) * a1) / ((p1.y - p2.y) * (p1.x - p3.y) - (p1.x - p2.x) * (p1.y - p3.y));
    O.y = ((p1.x - p3.x) * a1 - (p1.x - p2.x) * a2) / ((p1.y - p2.y) * (p1.x - p3.x) - (p1.x - p2.x) * (p1.y - p3.y));
    O.ok=1;
    return O;
}
 
int main(int argc, char const *argv[])
{
    int n;
    scanf ("%d",&n);
    for (int i=1; i<=n; i++){
        double x,y;
        scanf ("%lf%lf",&x,&y);
        a[i]=node{x,y};
    }
    if (n==1){
        printf("%d
",1);return 0;
    }
    a[0]=node{0,0};
    int ans=0;
    for (int i=1; i<=n; i++){
        int cnt=0;
        for (int j=1; j<=n; j++){
            if (i==j) continue;
            Point op=find(a[i],a[j],a[0]);
            if (!op.ok) continue;//debug;
            OS[++cnt]=op;
        }
        sort(OS+1,OS+1+cnt);
        int nb=0;
        for (int j=1; j<=cnt; j++){
            int k=j;
            while (fabs(OS[j].x-OS[k].x)<esp && fabs(OS[j].y-OS[k].y)<esp && k<=cnt) k++;
            if (k-j+1>nb){
                nb=k-j+1;
            }
            j=k;
        }
        ans=max(ans,nb);
    }
    printf("%d
",ans);
    return 0;
}

B.Boundary

题目大意：给你n个点，你需要找到一个过原点的圆，使得圆上的点最多，问最多有多少个点在圆上，n<=2000

输入

4
1 1
0 2
2 0
2 2

输出

3

emmm，我们首先需要知道的是三点可以确定一个圆，那么已经知道了一个原点，那么我们可以直接枚举另外的两个点，然后计算出圆心，然后取出圆心出现最多的那个点作为最终的圆心，再计算答案，只不过有点可怕的是，圆心的计算会出现小数，用map来保存圆心的话会被精度卡掉，我们可以先将所有的圆心存下来，然后排个序，再对它进行精度判断和出现次数判断。但也很遗憾的是这个操作也非常看脸和看姿势。。。可能我脸比较黑，姿势也不太对。。。只能过95%的数据。。。

以下是直接用double硬刚的代码：

#include <bits/stdc++.h>
using namespace std;
 
#define debug printf("@#$@$#@$##&*
")
const int mac=2e3+10;
const double esp=1e-9;
 
struct node
{
    double x,y;
}a[mac];
 
struct Point
{
    double x,y;
    int ok;
    bool operator <(const Point &a)const{
        if (fabs(x-a.x)<esp) return y<a.y;
        return x<a.x;
    }
};
Point OS[mac*mac];
  
Point find(node p1,node p2,node p3) {
    if(fabs((p1.x - p2.x) * (p1.y - p3.y) - (p1.x - p3.x) * (p1.y - p2.y)) <esp) {
        return Point{0,0,0};
    }
    double a1 = ((p1.x * p1.x - p2.x * p2.x) + (p1.y * p1.y - p2.y * p2.y)) / 2;
    double a2 = ((p1.x * p1.x - p3.x * p3.x) + (p1.y * p1.y - p3.y * p3.y)) / 2;
      
    Point O;
    O.x = ((p1.y - p2.y) * a2 - (p1.y - p3.y) * a1) / ((p1.y - p2.y) * (p1.x - p3.y) - (p1.x - p2.x) * (p1.y - p3.y));
    O.y = ((p1.x - p3.x) * a1 - (p1.x - p2.x) * a2) / ((p1.y - p2.y) * (p1.x - p3.x) - (p1.x - p2.x) * (p1.y - p3.y));
    O.ok=1;
    return O;
}
 
int main(int argc, char const *argv[])
{
    int n;
    scanf ("%d",&n);
    for (int i=1; i<=n; i++){
        double x,y;
        scanf ("%lf%lf",&x,&y);
        a[i]=node{x,y};
    }
    if (n==1){
        printf("%d
",1);return 0;
    }
    a[0]=node{0,0};
    double ox,oy;
    int cnt=0;
    for (int i=1; i<=n; i++)
        for (int j=i+1; j<=n; j++){
            Point op=find(a[i],a[j],a[0]);
            if (!op.ok) continue;//debug;
            OS[++cnt]=op;
        }
    sort(OS+1,OS+1+cnt);
    int nb=1,same=1;
    ox=OS[1].x; oy=OS[1].y;
    for (int i=1; i<=cnt; i++){
        int j=i;
        while (fabs(OS[i].x-OS[j].x)<esp && fabs(OS[i].y-OS[j].y)<esp){
            j++;
            if (j>cnt) break;
        }
        if (j-i+1>nb){
            nb=j-i+1;
            ox=OS[i].x;
            oy=OS[i].y;
        }
        i=j-1;
    }
    double dis=ox*ox+oy*oy;
    int ans=0;
    for (int i=1; i<=n; i++){
        double odis=(ox-a[i].x)*(ox-a[i].x)+(oy-a[i].y)*(oy-a[i].y);
        if (fabs(dis-odis)<esp) ans++;
    }
    printf("%d
",max(1,ans));
    return 0;
}

这里解释下为什么答案是圆心的个数+1，我们枚举的是$i$点在圆上，那么如果有$k$个相同的圆心，说明第$i$个点可以和$k$个点组成改圆，那么也就有$k+1$个点了。

然后开始用分数来搞了。。。。那就是重载套重载，四个关键字的排序，然后GCD，然后T了。。。QAQ，只过了70%的数据

以下是分数保存圆心的代码：

#include <bits/stdc++.h>
using namespace std;
 
#define debug printf("@#$@$#@$##&*
")
typedef long long ll;
const int mac=2e3+10;
const double esp=1e-9;
 
struct fenshu
{
    ll fz,fm;
    bool operator <(const fenshu &a) const{
        return fz*a.fm<a.fz*fm;
    }
    bool operator ==(const fenshu &b)const{
        return fz*b.fm==fm*b.fz;
    }
};

struct node
{
    int x,y;
}a[mac];
 
struct Point
{
    fenshu x,y;
    int ok;
    bool operator <(const Point &a)const{
        if (x==a.x) return y<a.y;
        return x<a.x; 
    }
    bool operator ==(const Point &b)const{
        return x==b.x && y==b.y;
    }
};
Point OS[mac*mac];
  
Point find(node p1,node p2,node p3) {
    if((p1.x - p2.x) * (p1.y - p3.y) == (p1.x - p3.x) * (p1.y - p2.y)) {
        return Point{fenshu{0,0},fenshu{0,0},0};
    }
    fenshu a1,a2;
    a1.fz=(p1.x * p1.x - p2.x * p2.x) + (p1.y * p1.y - p2.y * p2.y); a1.fm=2;
    a2.fz=(p1.x * p1.x - p3.x * p3.x) + (p1.y * p1.y - p3.y * p3.y); a2.fm=2;
      
    Point O;
    O.x.fz=(p1.y - p2.y)*a2.fz*a1.fm-(p1.y - p3.y)*a1.fz*a2.fm;
    O.x.fm=a1.fm*a2.fm*((p1.y - p2.y) * (p1.x - p3.y) - (p1.x - p2.x) * (p1.y - p3.y));

    O.y.fz=(p1.x - p3.x)*a1.fz*a2.fm-(p1.x - p2.x)*a2.fz*a1.fm;
    O.y.fm=a1.fm*a2.fm*((p1.y - p2.y) * (p1.x - p3.x) - (p1.x - p2.x) * (p1.y - p3.y));
   
    O.ok=1;
    ll p=__gcd(O.x.fz,O.x.fm); O.x.fz/=p; O.x.fm/=p;
    p=__gcd(O.y.fz,O.y.fm); O.y.fz/=p; O.y.fm/=p;
    return O;
}
 
int main(int argc, char const *argv[])
{
    int n;
    scanf ("%d",&n);
    for (int i=1; i<=n; i++){
        int x,y;
        scanf ("%d%d",&x,&y);
        a[i]=node{x,y};
    }
    if (n==1){
        printf("%d
",1);return 0;
    }
    a[0]=node{0,0};
    int ans=0;
    for (int i=1; i<=n; i++){
        int cnt=0;
        for (int j=1; j<=n; j++){
            if (i==j) continue;
            Point op=find(a[i],a[j],a[0]);
            if (!op.ok) continue;//debug;
            OS[++cnt]=op;
        }
        sort(OS+1,OS+1+cnt);
        Point O;
        int nb=0;
        for (int j=1; j<=cnt;){
            int k=j;
            while (k<=cnt && OS[j]==OS[k]) k++;
            if (k-j+1>nb) {
                nb=k-j+1;
            }
            j=k;
        }
        ans=max(ans,nb);
    }
    printf("%d
",ans);
    return 0;
}

说真的。。。。写到这里挺绝望的了，只能按照正解的找角度了来了。。。

后来某个巨佬对的AC代码给了我很大的启发，我看他的AC代码是用>esp的，于是我就将<esp改成>esp，然后做个相应的调整就过了。。。。#$#@齾@#$鵞@#$#@齾$@&*鵞&^*豟^&@鵞#!!@豟#

以下是double硬刚的AC代码：

#include <bits/stdc++.h>
using namespace std;
  
#define debug printf("@#$@$#@$##&*
")
const int mac=2e3+10;
const double inf=1e16+10;
const double esp=1e-8;
  
struct node
{
    double x,y;
}a[mac];
  
struct Point
{
    double x,y;
    int ok;
    bool operator <(const Point &a)const{
        if (fabs(x-a.x)<esp) return y<a.y;
        return x<a.x;
    }
};
Point OS[mac*mac];
   
Point find(node p1,node p2,node p3) {
    if(fabs((p1.x - p2.x) * (p1.y - p3.y) - (p1.x - p3.x) * (p1.y - p2.y)) <esp) {
        return Point{0,0,0};
    }
    double a1 = ((p1.x * p1.x - p2.x * p2.x) + (p1.y * p1.y - p2.y * p2.y)) / 2;
    double a2 = ((p1.x * p1.x - p3.x * p3.x) + (p1.y * p1.y - p3.y * p3.y)) / 2;
       
    Point O;
    O.x = ((p1.y - p2.y) * a2 - (p1.y - p3.y) * a1) / ((p1.y - p2.y) * (p1.x - p3.y) - (p1.x - p2.x) * (p1.y - p3.y));
    O.y = ((p1.x - p3.x) * a1 - (p1.x - p2.x) * a2) / ((p1.y - p2.y) * (p1.x - p3.x) - (p1.x - p2.x) * (p1.y - p3.y));
    O.ok=1;
    return O;
}
  
int main(int argc, char const *argv[])
{
    int n;
    scanf ("%d",&n);
    for (int i=1; i<=n; i++){
        double x,y;
        scanf ("%lf%lf",&x,&y);
        a[i]=node{x,y};
    }
    if (n==1){
        printf("%d
",1);return 0;
    }
    a[0]=node{0,0};
    int ans=0;
    for (int i=1; i<=n; i++){
        int cnt=0;
        for (int j=1; j<=n; j++){
            if (i==j) continue;
            Point op=find(a[i],a[j],a[0]);
            if (!op.ok) continue;//debug;
            OS[++cnt]=op;
        }
        sort(OS+1,OS+1+cnt);
        OS[cnt+1]=Point{inf,inf};
        int nb=0;
        for (int j=1; j<=cnt; j++){
            nb++;
            if (fabs(OS[j].x-OS[j+1].x)>esp || fabs(OS[j].y-OS[j+1].y)>esp){
                ans=max(ans,nb+1);
                nb=0;
            }
        }
        ans=max(ans,nb+1);
    }
    printf("%d
",ans);
    return 0;
}

 （角度正解之后再补啦^_^）

C. Cover the Tree

题目大意：给你一颗无根树，n个节点，问你最少能用多少条链将整棵树的每个边覆盖，输出链数和每条链的起点和终点。n<=2e5

输入

5
1 2
1 3
2 4
2 5

输出

2
2 3
4 5

实际上个数是确定的，也非常好求，就是叶子节点的个数除以2向上取整，也就是说我们将叶子节点两两配对就好了。接下来我们就直接做个dfs序，记录第$k$个叶子节点的编号，然后我们将第$i$个叶子节点和第$i+(sum+1)/2$个叶子节点配对就好了。其中sum表示叶子节点的数量。

以下是AC代码：

#include <bits/stdc++.h>
using namespace std;

const int mac=2e5+10;

struct node
{
    int to,next;
}eg[mac<<1];
int du[mac],leaf[mac],cnt=0,num=0;
int head[mac];

void add(int u,int v)
{
    eg[++num]=node{v,head[u]};
    head[u]=num;
}

void dfs(int x,int fa)
{
    if (du[x]==1) 
        leaf[++cnt]=x;
    for (int i=head[x]; i!=-1; i=eg[i].next){
        int v=eg[i].to;
        if (v==fa) continue;
        dfs(v,x);
    }
}

int main(int argc, char const *argv[])
{
    int n;
    memset(head,-1,sizeof head);
    scanf ("%d",&n);
    for (int i=1; i<n; i++){
        int u,v;
        scanf ("%d%d",&u,&v);
        du[u]++;du[v]++;
        add(u,v);add(v,u);
    }
    int root=1;
    for (int i=1; i<=n; i++) {
        if (du[i]>1) {root=i; break;}
    }
    dfs(root,-1);
    printf("%d
",(cnt+1)/2);
    for (int i=1; i<=cnt/2; i++)
        printf("%d %d
",leaf[i],leaf[i+(cnt+1)/2]);
    if (cnt&1)
        printf("%d %d
",root,leaf[(cnt+1)/2]);
    return 0;
}

D.Duration

题目大意：给你同一天的两个时间，问你他们的间隔是多少秒

输入

12:00:00
17:00:00

输出

18000

 

输入

23:59:59
00:00:00

输出

86399

emmm，这题是真的签到。。。直接将他们每个点到0点的时间计算一下，然后两个做差就完事了。

以下是AC代码：

#include <bits/stdc++.h>
using namespace std;

int main(int argc, char const *argv[])
{
    int h,m,s;
    int h1,m1,se;
    char s1[20],s2[20];
    cin>>s1;
    cin>>s2;
    h=(s1[0]-'0')*10+s1[1]-'0';
    m=(s1[3]-'0')*10+s1[4]-'0';
    s=(s1[6]-'0')*10+s1[7]-'0';

    h1=(s2[0]-'0')*10+s2[1]-'0';
    m1=(s2[3]-'0')*10+s2[4]-'0';
    se=(s2[6]-'0')*10+s2[7]-'0';
    int p1=s+m*60+h*60*60;
    int p2=se+m1*60+h1*60*60;
    cout<<abs(p1-p2)<<endl;
    return 0;
}

F.Fake Maxpooling

题目大意：给你n和m，代表了一个矩阵，其中元素的值为$a_{i,j}=lcm(i,j)$，然后给你一个k，问所有$k imes k$的子矩阵中最大值的和是多少。$n,m<=5000$

输入

3 4 2

输出

38

emmm，也是比较水的一题，一眼望去就知道是个二维区间最值问题，我们先将矩阵$a$求出来，然后跑区间最值就OK了，只不过二维RMQ会又T又MLE，所以我们要换种更加高效的方法，那么就是单调队列了。实际上单调队列维护二维最值是一个很经典的问题。同一维的最值并没有太大从差别。

我们先用单调队列维护一下每行中区间大小为$k$的最大值，然后再用单调队列维护每列中已经维护了的$k$行，说起来有点绕，实际上就是先用单调队列维护一下矩阵$a$的每行$k$长度的最大值得到$mx[i][j]$表示第$i$行从第$j$列开始到$(i,j+k-1)$的最值，然后再用单调队列维护矩阵$mx$的每列。具体详情可见代码

以下是AC代码：

#include <bits/stdc++.h>
using namespace std;

typedef long long ll;
const int mac=5e3+10;

struct node
{
    int val,id;
}que[mac];

int a[mac][mac],mx[mac][mac];

int lcm(int x,int y)
{
    return x/__gcd(x,y)*y;
}

void solve(int n,int m,int len)
{
    for (int i=1; i<=n; i++){//维护每行的区间len的最大值
        int head=1,tail=0,p=1;
        while (head>tail || p<=len){
            if (head>tail) {que[++tail].val=a[i][p]; que[tail].id=p++; continue;}
            while (head<=tail && que[tail].val<a[i][p]) tail--;
            que[++tail]=node{a[i][p],p};
            p++;
        }
        mx[i][1]=que[1].val;
        for (int j=p; j<=m; j++){
            while (head<=tail && j-que[head].id+1>len) head++;
            if (head>tail) {que[++tail]=node{a[i][j],j}; mx[i][j-len+1]=que[head].val; continue;}
            while (head<=tail && que[tail].val<a[i][j]) tail--;
            que[++tail]=node{a[i][j],j};
            mx[i][j-len+1]=que[head].val;
        }
    }
    for (int j=1; j<=m-len+1; j++){//维护每列len行最大值的最大值
        int head=1,tail=0,p=1;
        while (head>tail || p<=len){
            if (head>tail) {que[++tail].val=mx[p][j]; que[tail].id=p++; continue;}
            while (head<=tail && que[tail].val<mx[p][j]) tail--;
            que[++tail]=node{mx[p][j],p};
            p++;
        }
        mx[1][j]=que[1].val;
        for (int i=p; i<=n; i++){
            while (head<=tail && i-que[head].id+1>len) head++;
            if (head>tail) {que[++tail]=node{mx[i][j],i}; mx[i-len+1][j]=que[head].val; continue;}
            while (head<=tail && que[tail].val<mx[i][j]) tail--;
            que[++tail]=node{mx[i][j],i};
            mx[i-len+1][j]=que[head].val;
        }
    }
}

int main(int argc, char const *argv[])
{
    int n,m,len;
    scanf ("%d%d%d",&n,&m,&len);
    for (int i=1; i<=n; i++)
        for (int j=1; j<=m; j++)
            a[i][j]=lcm(i,j);
    solve(n,m,len);
    ll ans=0;
    for (int i=1; i<=n-len+1; i++)
        for (int j=1; j<=m-len+1; j++){
            ans+=mx[i][j];
        }
    printf("%lld
",ans);
    return 0;
}

G.Greater and Greater

题目大意：给你一个长度为n的序列A和一个长度为m序列B，让你在第一个序列中找到子区间使得子区间$S_i>=B_i$问有多少个这样的子区间，$n<=1.5e5,m<=4e4$

输入

6 3
1 4 2 8 5 7
2 3 3

输出

2

emmmm，最原始的办法就是暴力查找。。。。时间复杂度为$O(nm)$在此数据下会T飞。

接下来我们考虑$bitset$，没错，我并不知道为什么会想到这玩意儿QAQ。

我们先$have$ $a$  $try$一波，对样例进行操作，很明显按照题解所说的，构造$bitset$，对于A的每个位置构造一个长度为m的$bitset$，那么所构造出来的就是：

000   111   100   111   111   111

将其按照顺序排列就是：

111

  111

    111

      100

        111

          000

那么如上图所示，只有竖着下来m个全是1的时候才会是一个合法区间。那么我们枚举序列B，对于A中每一个大于B的元素，我们将1放入$bitset$中A中该元素的位置，即$g.set(a[i].id)$也就是说这个$a[i].id$这个位置我们已经放入了元素1。

对于排完序的A，我们一直找下去，就会得到一个所有大于$B_i$的完整的$bitset$，接下来我们将这个$bitset$右移$b[i].id$个位置，表示要从这个位置开始，然后对$bitset<>f$取&运算（初始状态$f$为满1），那么如果该位置为是不行的也就是0，那么上一个f的该位置就会被清理掉，那么经过m次重复操作后，$f$剩下的就是合法区间的开始位置了，这个操作就是一直往回退，每次退到开始的位置进行判断，经过m次后如果该起点是OK的，那么就一定是OK的了。如下图所示：

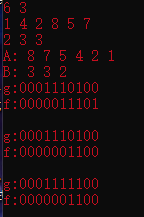
以下是AC代码：

#include <bits/stdc++.h>
using namespace std;

const int mac=2e5+10;
const int maxn=4e4+10;

struct node
{
    int val,id;
    bool operator <(const node&a)const{
        return val>a.val;
    }
};
node a[mac],b[maxn];
bitset<mac>f,g;

int main(int argc, char const *argv[])
{
    int n,m,x;
    scanf ("%d%d",&n,&m);
    for (int i=1; i<=n; i++){
        scanf ("%d",&x);
        a[i]=node{x,i};
    }
    for (int i=1; i<=m; i++){
        scanf ("%d",&x);
        b[i]=node{x,i};
    }
    sort(a+1,a+1+n);
    sort(b+1,b+1+m);
    f.set();g.reset();//f刚开始全部为1,g全为0
    for (int i=1,j=1; i<=m; i++){
        while (j<=n && a[j].val>=b[i].val) g.set(a[j++].id);//a[j].val所在的位置标记为1
        f&=g>>b[i].id;
    }
    printf("%d
",f.count());
    return 0;
}

H.Happy Triangle 

题目大意：有一个空的集合，你有三个操作，操作1为加入一个元素x，操作2为删除一个元素x，操作三为询问在集合内是否能够找到两个元素使得和$x$能构成一个非退化的三角形。

输入

8
1 1
3 1
1 1
3 2
3 1
1 2
2 1
3 1

输出

No
No
Yes
No

我们可以设拿出来的两个元素为$a,b(a<=b)$，要想组成一个非退化的三角形，那么有两种情况，一是x为最大值，那么判断一下$a+b>x$就完事了，这个可以用简单的map来维护，map做的是将x映射到其数量上：

int ok_max(int x)
{
    if (mp.empty()) return 0;
    auto it=mp.lower_bound(x);
    if (it==mp.end() || it->first>x){//二分找到的数大于x，或x大于所有的数
        if (it==mp.begin()) return 0;//如果二分找到的数大于x且没有比他小的数
        --it;
        if (it->second>1){
            if (it->first>=x/2+1) return 1;
            return 0;
        } 
        if (it==mp.begin()) return 0;
        int a=it->first;
        --it;
        if (a+it->first>x) return 1;
        return 0;
    }

    if (it->first==x){
        if (it->second>1) return 1;
        if (it==mp.begin()) return 0;
        return 1;
    }
}

接下来就是第二种情况，这种情况比较麻烦，也就是x不是最大边的情况，那么我们就要去找每一对相邻的$b-a$，并判断他们的差值是否小于x。实际上我们可以用线段树来维护每个数和其前驱的差值，那么对于x不是最大边的情况我们只需要在区间$[x+1,max]$中寻找一个最小差值就可以了。

那么接下来就是比较关键的了，我们要怎么来维护每个数和其前驱的差值？这个就需要map和线段树配合的一系列操作了。我们知道，每插入一个数，只会对自身和后继产生差值的变化，每删除一个数也之会对自身和后继的差值产生变化。那么我们每次操作的时候求一个x的前驱，判断一下x的后继是否只有1个，然后就可以直接更改x位置和后继的最小差值了，如下所示：

void insert_x(int x)
{
    mp[x]++;
    int pre=-inf;
    if (mp[x]==1){
        auto it=mp.lower_bound(x);
        if (it!=mp.begin()){//求x的前驱
            --it;
            pre=it->first;
            ++it;
        }
        update(1,inf,root,x,x-pre);
        ++it;
        if (it!=mp.end() && it->second==1)//如果后继只有一个
            update(1,inf,root,it->first,it->first-x);
    }
    else if (mp[x]==2) update(1,inf,root,x,0);
}

void eraser_x(int x)
{
    auto it=mp.lower_bound(x);
    mp[x]--;
    int pre=-inf;
    if (it!=mp.begin()){//求x的前驱
        --it;
        pre=it->first;
        ++it;
    }
    if (mp[x]==0){
        ++it;
        if (it!=mp.end() && it->second==1)//如果后继只有一个
            update(1,inf,root,it->first,it->first-pre);
        update(1,inf,root,x,inf);
        mp.erase(x);
    }
    else if (mp[x]==1) update(1,inf,root,x,x-pre);
}

然后update函数也就没什么好说的了，就是个单点更新的操作，只不过需要注意的是动态开点的话需要的空间比较大，不再是线段树的maxn*4了，我忘了这个东西了，一直段错误QAQ。。。

以下是AC代码：

#include <bits/stdc++.h>
using namespace std;

#define lson l,mid,tree[rt].l
#define rson mid+1,r,tree[rt].r
#define lc tree[rt].l
#define rc tree[rt].r
const int mac=2e5+10;
const int inf=1e9+50;

struct node
{
    int l,r,dif;
}tree[mac*40];
int sz=0,root=0;
map<int,int>mp;

void push_up(int rt)
{
    int ans=inf;
    if (tree[rt].l) ans=min(ans,tree[lc].dif);
    if (tree[rt].r) ans=min(ans,tree[rc].dif);
    tree[rt].dif=ans; 
}

void update(int l,int r,int &rt,int pos,int val)
{
    if (!rt) rt=++sz;
    if (l==r) {tree[rt].dif=val; return;}
    int mid=(l+r)>>1;
    if (mid>=pos) update(lson,pos,val);
    else update(rson,pos,val);
    push_up(rt);
}

void insert_x(int x)
{
    mp[x]++;
    int pre=-inf;
    if (mp[x]==1){
        auto it=mp.lower_bound(x);
        if (it!=mp.begin()){
            --it;
            pre=it->first;
            ++it;
        }
        update(1,inf,root,x,x-pre);

        ++it;
        if (it!=mp.end() && it->second==1)
            update(1,inf,root,it->first,it->first-x);
    }
    else if (mp[x]==2) update(1,inf,root,x,0);
}

void eraser_x(int x)
{
    auto it=mp.lower_bound(x);
    mp[x]--;
    int pre=-inf;
    if (it!=mp.begin()){
        --it;
        pre=it->first;
        ++it;
    }
    if (mp[x]==0){
        ++it;
        if (it!=mp.end() && it->second==1)
            update(1,inf,root,it->first,it->first-pre);
        update(1,inf,root,x,inf);
        mp.erase(x);
    }
    else if (mp[x]==1) update(1,inf,root,x,x-pre);
}

int ok_max(int x)
{
    if (mp.empty()) return 0;
    auto it=mp.lower_bound(x);
    if (it==mp.end() || it->first>x){
        if (it==mp.begin()) return 0;
        --it;
        if (it->second>1){
            if (it->first>=x/2+1) return 1;
            return 0;
        } 
        if (it==mp.begin()) return 0;
        int a=it->first;
        --it;
        if (a+it->first>x) return 1;
        return 0;
    }

    if (it->first==x){
        if (it->second>1) return 1;
        if (it==mp.begin()) return 0;
        return 1;
    }
}

int query(int l,int r,int rt,int L,int R)
{
    int ans=inf;
    if (l>=L && r<=R) return tree[rt].dif;
    int mid=(l+r)>>1;
    if (mid>=L && tree[rt].l) ans=min(ans,query(lson,L,R));
    if (mid<R && tree[rt].r) ans=min(ans,query(rson,L,R));
    return ans;
}

int main(int argc, char const *argv[])
{
    int q;
    scanf ("%d",&q);
    while (q--){
        int op,x;
        scanf ("%d%d",&op,&x);
        if (op==1) insert_x(x);
        else if (op==2) eraser_x(x);
        else {
            if (ok_max(x)) printf("Yes
");
            else {
                if (query(1,inf,1,x+1,inf)<x) printf("Yes
");
                else printf("No
");
            }
        }
    }
    return 0;
}

I.Interval

题目大意：（吐槽-真的恶心，完全懵逼，事后找嫖老板问了下题意。。才知道我完全没理解题目QAQ）给你一个$n imes n$的方格，你初始位置是在$(1,n)$这个点，你每次可以有两种选择，一个是上下走，一个是左右走，你有m条禁令，$l$  $r$  $dir$  $cost$表示点$(l,r)$被禁止的方式，如果$dir$是$L$那么，从$(l,r)->(l+1,r)$是不被允许的，反过来也是被禁止的，如果$dir$是$R$，那么从$(l,r)->(l,r+1)$是不被允许的，反过来也是一样，而你需要发布禁止使得你无法到达$l=r$的点。求这个最小花费，如果无法完成任务，输出-1。

输入

3 4
1 3 L 10
1 3 R 3
1 2 L 1
1 2 R 1

输出

12

输入

2 1
1 2 L 1

输出

-1

emmm，实际上就是最小割，割除一些边使得其无法到达指定的点，我们可以先用网络流跑一波暴力的，注意禁令是双向的，那么建边也是双向的，最后将n个点汇聚到汇点的时候无所谓，可以单向，而点的数量我们可以只取网格的一半，因为前面的点是无用的，所以可以很大程度上优化一定的时间，然后。。。。过了80%的数据，本来还想着看看能不能直接暴力的。。。看来还是要跑一波对偶图的最短路。

以下是网络流做法（过80%，T了）

#include <bits/stdc++.h>
using namespace std;

typedef long long ll;
const int mac=1e6+10;
const int maxn=5e5+10;
const ll inf=1e15+10;

struct Edge
{
    int to,next;
    ll w;
}eg[mac<<1];
int head[maxn],num=0,dis[maxn],cur[maxn];
int S,T,a[550][550];
map<pair<int,int>,int>mp;

inline void add(int u,int v,ll w)
{
    if (mp[{u,v}]) return;
    eg[num]=Edge{v,head[u],w};
    head[u]=num++;
    eg[num]=Edge{u,head[v],0};
    head[v]=num++;
}

inline int bfs()
{
    queue<int>q;
    memset(dis,0,sizeof dis);
    dis[S]=1;
    q.push(S);
    while (!q.empty()){
        int u=q.front();
        q.pop();
        for (int i=head[u]; i!=-1; i=eg[i].next){
            int v=eg[i].to;
            if (eg[i].w>0 && dis[v]==0){
                dis[v]=dis[u]+1;
                if (v==T) return 1;
                q.push(v);
            }
        }
    }
    return 0;
}

inline ll dfs(int u,ll flow)
{
    if (u==T || !flow) return flow;
    ll sum=0,x=0;
    for (int i=cur[u]; i!=-1; i=eg[i].next){
        int v=eg[i].to;
        if (eg[i].w>0 && dis[v]==dis[u]+1){
            x=dfs(v,min(flow-sum,eg[i].w));
            eg[i].w-=x;
            eg[i^1].w+=x;
            if (eg[i].w) cur[u]=i;
            sum+=x;
            if (sum==flow) return flow;
        }
    }
    if (sum==0) dis[u]=0;
    return sum;
}

inline ll dinic(int n)
{
    ll sum=0;
    while (bfs()){//printf("@#$#$#@
");
        for (int i=1; i<=n; i++)
            cur[i]=head[i];
        sum+=dfs(S,inf);
    }
    return sum;
}

int main()
{
    memset(head,-1,sizeof head);
    int n,m,id=0;
    scanf ("%d%d",&n,&m);
    for (int i=1; i<=n; i++)
        for (int j=n; j>=1; j--)
            a[i][j]=++id;
    S=a[1][n]; T=id+1;
    for (int i=1; i<=m; i++){
        int l,r,w;
        char s[3];
        scanf ("%d%d%s%d",&l,&r,s,&w);
        if (s[0]=='L'){
            if (l<n){
                add(a[l][r],a[l+1][r],w);
                add(a[l+1][r],a[l][r],w);
                mp[make_pair(a[l][r],a[l+1][r])]=1;
                mp[make_pair(a[l+1][r],a[l][r])]=1;
            } 
        }
        else {
            if (r>1){
                add(a[l][r],a[l][r-1],w);
                add(a[l][r-1],a[l][r],w);
                mp[make_pair(a[l][r],a[l][r-1])]=1;
                mp[make_pair(a[l][r-1],a[l][r])]=1;
            } 
        }
    }
    for (int i=1; i<n; i++){
        for (int j=n; j>i; j--){
            pair<int,int>pt;
            pt.first=a[i][j]; pt.second=a[i][j-1];
            if (!mp[pt]) add(a[i][j],a[i][j-1],inf),add(a[i][j-1],a[i][j],inf);
            pt.second=a[i+1][j];
            if (!mp[pt]) add(a[i][j],a[i+1][j],inf),add(a[i+1][j],a[i][j],inf);
        }
    }
    for (int i=1; i<=n; i++) add(a[i][i],T,inf);
    ll ans=dinic(T);
    if (ans>=inf) printf("-1
");
    else printf("%lld
",ans);
    //printf("%lld
", ans);
    return 0;
}

然后要开始跑对偶图了，网上有挺多教程的可以学习一波，推荐一下https://www.cnblogs.com/lher/p/7856451.html（这是BZOJ上狼抓兔子的那题）

然后我们可以对图形编号并观察，如下所示：

 实际上紫色的边是没有作用的，可以直接忽略，然后我们可以观察对偶图的点和原来的点之间的关系，和割边的时候的编号关系。

然后我们会发现当禁止的边为竖边且在最后一列的时候，全部连到终点， 不在最后一列，那么左右点相连即可割去该边，当禁止的边为横边的时候，如果在第一行，那么全部连到起点，否则的话，上下点相连即可割去该边。

那么建边如下：

for (int i=1; i<n; i++)
    for (int j=i; j<n; j++)
        a[i][j]=++id;
int S=++id,T=++id;
for (int i=1; i<=m; i++) {
    int l,r,w;
    char s[3];
    scanf ("%d%d%s%d",&l,&r,s,&w);
    if (s[0]=='L') {
        if (r==n) add(a[l][n-1],T,w);
        else add(a[l][r-1],a[l][r],w);//左右点割去竖边
    } else {
        if (l==1) add(a[l][r-1],S,w);
        else add(a[l][r-1],a[l-1][r-1],w);//上下点割去横边
    }
}

然后我们对着边跑最短路就完事了。

以下是AC代码：

#include <bits/stdc++.h>
using namespace std;

typedef long long ll;
const int mac=1e6+10;
const ll inf=2e12;
const int maxn=3e5+10;

struct Edge
{
    int to,next;
    ll w;
}eg[mac<<1];
struct node
{
    int id;
    ll s;
    bool operator<(const node&a)const{
        return s>a.s;
    }
};
int a[550][550];
int head[maxn],num,vis[mac];
ll dis[maxn];

void add(int u,int v,ll w)
{
    eg[num]=Edge{v,head[u],w};
    head[u]=num++;
    eg[num]=Edge{u,head[v],w};
    head[v]=num++;
}

ll dij(int s,int t)
{
    for (int i=1; i<=t; i++) dis[i]=inf;
    dis[s]=0;
    priority_queue<node>q;
    q.push(node{s,0});
    while (!q.empty()){
        node now=q.top();
        q.pop();
        int u=now.id;
        if (vis[u]) continue;
        vis[u]=1;
        for (int i=head[u]; i!=-1; i=eg[i].next){
            int v=eg[i].to;
            if (!vis[v] && dis[v]>dis[u]+eg[i].w){
                dis[v]=dis[u]+eg[i].w;
                q.push(node{v,dis[v]});
            }
        }
    }
    return dis[t];
}

int main()
{
    memset(head,-1,sizeof head);
    int n,m,id=0;
    scanf ("%d%d",&n,&m);
    for (int i=1; i<n; i++)
        for (int j=i; j<n; j++)
            a[i][j]=++id;
    int S=++id,T=++id;
    for (int i=1; i<=m; i++){
        int l,r,w;
        char s[3];
        scanf ("%d%d%s%d",&l,&r,s,&w);
        if (s[0]=='L'){
            if (r==n) add(a[l][n-1],T,w);
            else add(a[l][r-1],a[l][r],w);//左右点割去竖边
        }
        else {
            if (l==1) add(a[l][r-1],S,w);
            else add(a[l][r-1],a[l-1][r-1],w);//上下点割去横边
        }
    }
    ll ans=dij(S,T);
    if (ans>=inf) printf("-1
");
    else printf("%lld
",ans);
    return 0;
}

J.Just Shuffle

题目大意：有一个初始序列为1-n的序列，现在给你一个序列为最终序列，让你求一个变化序列使得初始序列通过k次变化序列的变化变成最终序列$n<=1e5,kepsilon [1e8,1e9]$且k是个素数

输入

3 998244353
2 3 1

输出

3 1 2

emmm，题目可以看的不是很明白，不过没关系，我们可以手动来一波，初始序列为1 2 3，那么通过3 1 2的变化后得到第一次变化序列：1->3    2->1   3->2,也就成了3 1 2，再次变化就成了2 3 1，再次变化就回到了1 2 3.

那么刚开始看的时候确实很迷。。。。不过搞成数学的形式之后。。。。就感觉好简单了QAQ

通过一次变化的变化到最终串的我们称之为最终变化序列设为$B$，而现在要做的事情就是找一个小变化$A$通过$k$次之后到$B$，那么可以等价为$A^k=B$，求A。

那么我们将等式两边同乘以$t$可得$A^{kt}=B^t$，那么当$frac{1}{k}$的时候，我们就可以得到变化序列A了，那么在对于这个东西我们可以求$k$的逆元来代替，也就是说当$t=inv(k)$则有$A=B^t$

那么问题就来了，既然有逆元，那么模数在哪里呢？这个可能有点伤脑筋。。。实际上我们对B中的每个点求得的环就是这个模数，什么意思呢，拿样例来讲，第一个点的环就是第一个点通过若干次变化再一次回到原来位置这个过程，那么也就是说第一个环的大小为3，即可以如下模拟：

vector<int>round;
int pos=i;
while (!vis[pos]) {
    round.push_back(pos);
    vis[pos]=1;
    pos=a[pos];
}

那么这个环的大小就是模数了，我们对$t$从1开始找，找到一个$t*kmodsize==1$的就算是找到了，然后我们将环上的每个点向右移动$t$的单位，那么就得到了每个环上节点在$B^t$下的位置了。。。至于无解的情况，在这个k下是没有的，无解的情况就是存在环的大小和k不互质，那么就会有一些点无法找到

以下是AC代码：

#include <bits/stdc++.h>
using namespace std;

const int mac=1e5+10;

int a[mac],vis[mac],ans[mac];

int main(int argc, char const *argv[])
{
    int n,k;
    scanf ("%d%d",&n,&k);
    for (int i=1; i<=n; i++)
        scanf ("%d",&a[i]);
    for (int i=1; i<=n; i++){
        if (vis[i]) continue;
        vector<int>round;
        int pos=i;
        while (!vis[pos]){
            round.push_back(pos);
            vis[pos]=1;
            pos=a[pos];
        }
        int sz=round.size();
        int t=0;
        while (t<sz){
            if (1LL*t*k%sz==1) break;
            t++;
        }
        for (int j=0; j<sz; j++)
            ans[round[j]]=round[(j+t)%sz];
    }
    for (int i=1; i<=n; i++)
        printf("%d%c",ans[i],i==n?'
':' ');
    return 0;
}