题目链接:https://ac.nowcoder.com/acm/contest/3006#question
每场都非常的稳。。。稳的辣鸡
题目说明:
A.模板 B.牛牛战队的比赛地 C.C语言IDE D.牛牛与牛妹的约会
(贪心) (三分) (大模拟) (贪心)
E.Enjoy the game F.碎碎念 G.街机争霸 H.Hash
(找规律) (DP) (BFS) (字符串水题)
I.I题是个签到题 J.牛牛战队的秀场
(水题) (思维)
A.模板
题目大意:两个字符串互变,问至少要多少步,变化规则:
- 将其中任意一个字母替换为另一个
- 把最后一个字母删除
- 在尾部添加一个字母
示例
输入
4 3 WXYZ WXY
输出
1
没什么好说的,先把长度变成一样长,那么就需要$len(a)-len(b)$步,接下来就是将所有不一样字母的个数加起来就好了
以下是AC代码:

#include <bits/stdc++.h> using namespace std; const int mac=1e5+10; char s1[mac],s2[mac]; int main(int argc, char const *argv[]) { int n,m; scanf ("%d%d",&n,&m); scanf ("%s%s",s1,s2); int ans=max(n,m)-min(n,m); for (int i=0; i<min(n,m); i++){ if (s1[i]!=s2[i]) ans++; } printf("%d ",ans); return 0; }
B.牛牛战队的比赛地、
题目大意:在x轴上找一点,使得其距离n个点的最大距离最小
示例
输入
3 0 0 2 0 0 2
输出
2
。。。。没注意看题,然后写了个三分套三分,然后发现输出是个$sqrt{2}$。。。。然后就发现固定在了x轴,那么我们直接三分x轴就好了。不过为了增加精度,我们最后再开方。
以下是AC代码:

#include <bits/stdc++.h> using namespace std; const int mac=1e5+10; const int inf=1e9+10; struct node { int x,y; }pt[mac]; int n; double sans=inf; double dis(double x) { double ans=0; for (int i=1; i<=n; i++){ double dist=(x-pt[i].x)*(x-pt[i].x)+(pt[i].y)*(pt[i].y); ans=max(ans,dist); } sans=min(sans,ans); return ans; } int main(int argc, char const *argv[]) { scanf ("%d",&n); int xma=-inf,xmi=inf,yma=-inf,ymi=inf; for (int i=1; i<=n; i++){ int x,y; scanf ("%d%d",&x,&y); pt[i]=node{x,y}; xma=max(x,xma);xmi=min(x,xmi); yma=max(y,yma);ymi=min(y,ymi); } double lx=xmi,rx=xma,ly=ymi,ry=yma; for (int i=1; i<=50; i++){ double mid1=(lx+rx)/2; double mid2=(mid1+rx)/2; ly=ymi,ry=yma; if (dis(mid1)<dis(mid2)) rx=mid2; else lx=mid1; } printf("%.5f ",sqrt(sans)); return 0; }
C.C语言IDE
题目大意:
示例
输入
#include <stdio.h>
int plus(int a, int b)
{
return a + b;
}
int main()
{
int a,b;
scanf("%d%d", &a, &b);
printf("%d
", plus(a, b));
return 0;
}
输出
int plus(int,int) int main()
D.牛牛与牛妹的约会
题目大意:T组数据(5e5)给你$a,b$两点,你要从$a$到$b$,你可以花费1距离/1单位时间,也可以花费1单位时间从$x$位置到$sqrt[3]{x}$,问你a到b的最少时间。
示例
输入
2 3 -1 1 2
输出
3.442249570 1.000000000
每次走的时候比较直接走和闪现那个更优就行了,如果直接走比闪现更优,说明之后都是直接走更优了,我们break,注意一下pow函数需要对负数特殊处理
以下是AC代码:

#include <bits/stdc++.h> using namespace std; int main(int argc, char const *argv[]) { int t; scanf ("%d",&t); while (t--){ int a,b; scanf ("%d%d",&a,&b); double x=a,y=b,nx; double ans=0; while(1){ if (x<0) nx=-pow(-x,1.0/3.0); else nx=pow(x,1.0/3.0); if (fabs(nx-y)<fabs(x-y)-1) ans+=1,x=nx;//比较两个谁更优 else {ans+=fabs(x-y); break;} } printf("%.8f ",ans); } return 0; }
E.Enjoy the game
题目大意:Bob和Alice博弈,规则如下:
- 初始一共有n张卡牌
- 先手第一步最少要拿1张牌,最多要拿n-1张牌。
- 接下来每一步,双方最少要拿1张牌,最多拿等同于上一步对方拿的牌数的牌。
- 拿走最后一张牌的人将取得游戏的胜利。
示例
输入
2
输出
Alice
这题,找规律。。。没什么好说的,大胆尝试,交他一发,然后证明了$2^{k}$则Alice获胜,否则就是Bob
以下是AC代码:

#include <bits/stdc++.h> using namespace std; int main(int argc, char const *argv[]) { long long n; cin>>n; int mark=0; while (n>1){ if (n&1) mark=1; n>>=1; } if (mark) cout<<"Bob"<<endl; else cout<<"Alice"<<endl; return 0; }
F.碎碎念
题目大意:AC一道题会说一句话,RJ一道题会说$x$句话,问,如果他说了$[l,r]$句话,那么他有几种有效提交序列
示例
输入
3 3 3 3 1 4 1 5
输出
2 7 11
一眼DP。。。我们的第$i$句话肯定是由第$i-1$和第$i-x$句或转移过去的那么我们只需要想想怎么转移过去了,我们设$dp[i][0/1]$($dp[i][0]$表示$i-1$句话AC到i),然后$i-x$只能AC状态转移过去即:
$dp[i][0]=dp[i-1][0]+dp[i-1][1]$
$dp[i][1]=dp[i-x][0]$
以下是AC代码:

#include <bits/stdc++.h> using namespace std; typedef long long ll; const ll mod=1e9+7; const int mac=1e5+10; ll dp[mac][5]; int main(int argc, char const *argv[]) { int x,q; scanf ("%d%d",&x,&q); dp[0][0]=1; for (int i=1; i<mac; i++){ if (i<x) dp[i][0]=(dp[i-1][0]+dp[i-1][1])%mod; else { dp[i][0]=(dp[i-1][0]+dp[i-1][1])%mod; dp[i][1]=(dp[i-x][0])%mod; } dp[i][2]=(dp[i][0]+dp[i][1])%mod; dp[i][2]=(dp[i][2]+dp[i-1][2])%mod; } while (q--){ int l,r; scanf ("%d%d",&l,&r); ll ans=dp[r][2]-dp[l-1][2]; ans=(ans+mod)%mod; printf("%lld ",ans); } return 0; }
G.街机争霸
题目大意:
示例
输入
3 3 1 3 &&A ### &&L 2 1 RIGHT
输出
2
H.Hash
题目大意:给你一个长度为6的字符串和hash值的mod,让你构造一个一样长的字符串,字典序大于原来的,使得其hash值与原来的一样
示例
输入
abcdef 11
输出
abcdeq
。。。实际上就是个26进制的的加法,我们在原来的Hash值上直接加上mod就好了,然后就开始进位就好了
以下是AC代码:

#include <bits/stdc++.h> using namespace std; const int LEN = 6; char s[10]; int mod,p[10]; void solve() { for(int i=0; i<6; i++) printf("%c",p[i]+'a'); printf(" "); } int main(int argc, char const *argv[]) { while (~scanf ("%s%d",s,&mod)){ for (int i=0; i<6; i++) p[i]=s[i]-'a'; p[5]+=mod; if (p[5]<26) {solve(); continue;} p[4]+=p[5]/26; p[5]%=26; if (p[4]<26) {solve(); continue;} p[3]+=p[4]/26; p[4]%=26; if (p[3]<26) {solve(); continue;} p[2]+=p[3]/26; p[3]%=26; if (p[2]<26) {solve(); continue;} p[1]+=p[2]/26; p[2]%=26; if (p[1]<26) {solve(); continue;} p[0]+=p[1]/26; p[1]%=26; if (p[0]<26) {solve(); continue;} printf("-1 "); } return 0; }
I.I题是个签到题
题目大意:给你n,m(题目数量,总人数)和n道题的过题人数,然后让你判断I题是否是签到题(有80%的人过了或者过题人数前3名的)
示例
输入
9 100 100 100 100 100 100 100 100 100 100
输出
Yes
这题确实是个签到题。。。不过需要注意的是人数会有小数点所以要特判一下。。。我就是这里被卡了10来min。。。。
以下是AC代码:

#include <bits/stdc++.h> using namespace std; int a[20]; bool cmp(int x,int y) { return x>y; } int main(int argc, char const *argv[]) { int n,m; scanf ("%d%d",&n,&m); int nb=m*0.8; if (4*m%5) nb++;//!注意 int mark=0,val; for (int i=1; i<=n; i++){ int x; scanf ("%d",&x); a[i]=x; if (i==9) val=x; if (i==9 && x>=nb) mark=1; } sort(a+1,a+1+n,cmp); if (mark) printf("Yes "); else { if (val>=a[3]) printf("Yes "); else printf("No "); } return 0; }
J.牛牛战队的秀场
题目大意:给你正n边形和其外接圆的半径,问你从第i个顶点到第j个顶点的最短路径是多少(编号是从1开始顺时针编号)
示例
输入
4 1 1 2
输出
1.414214
题目理解错了,我以为只能顺时针走。。。。然后卡了好久。。。我们先算出这个正n边形的边长,这个很好算:
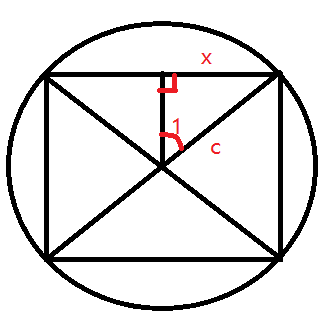
n边形可以分解成n个一模一样的等腰三角形,一个等腰三角形又可以拆成2个一模一样的直角三角形,那么角1的度数就很好算了:$angle 1=frac{360}{2n}=frac{pi }{n}$
那么根据三角函数,$x$也就出来了:$x=2rsinangle 1$
最后我们取顺时针到j点和逆时针到j点的最小值
以下是AC代码:

#include <bits/stdc++.h> using namespace std; const double pi=acos(-1); int main(int argc, char const *argv[]) { int n,r; scanf ("%d%d",&n,&r); int i,j; scanf ("%d%d",&i,&j); double a=pi/n; double len=2.0*r*sin(a); double ans1,ans2; ans1=len*n; ans1-=1.0*abs(i-j)*len; ans2=1.0*abs(i-j)*len; printf("%.7f ",min(ans1,ans2)); return 0; }
