题目链接:http://acm.csust.edu.cn/problem/3033
Description
定义![]() ,即1到i的j次方的异或和
,即1到i的j次方的异或和
求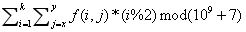 的值
的值
Input
一行三个整数k,x,y
1≤k≤1e5
1≤x≤y≤1e9
Output
一个整数,表示答案
Sample Input 1
1 2 7
Sample Output 1
6
此题看起来复杂,但打个表就会发现是个一眼题... 公式由于(i%2)的存在,所以我们只需要计算i为奇数的情况就好了。 那么打个奇数的表就会发现:

那么此题就结束了。
证明如下:
记 f(x, y) 为x到y的所有整数的异或值。对 f(2^k, 2^(k+1) -1) (注意文章中的 ^ 表示的是“幂”,xor 表示“异或”,or 表示“或”): 2^k 到 2^(k+1) -1 这2^k个数,最高位(+k位)的1个数为2^k, 若 k >= 1,则2^k为偶数,将这2^k个数的最高位(+k位)去掉,异或值不变。
因而f(2^k, 2^(k+1) -1) = f(2^k - 2^k, 2^(k+1) -1 -2^k) = f(0, 2^k -1)
因而 f(0, 2^(k+1) -1) = f(0, 2^k -1) xor f(2^k, 2^(k+1) -1) = 0 (k >= 1) 即 f(0, 2^k - 1) = 0 (k >= 2)
对 f(0, n) (n >= 4) 设n的最高位1是在+k位(k >= 2), f(0, n) = f(0, 2^k - 1) xor f(2^k, n) = f(2^k, n) 对2^k到n这n+1-2^k个数,最高位(+k位)共有 m = n+1-2^k 个1,去除最高位的1 当n为奇数时,m是偶数,
因而 f(0, n) = f(2^k, n) = f(0, n - 2^k) 由于n - 2^k 与 n同奇偶,递推上面的公式,可得:
f(0, n) = f(0, n % 4)
当 n % 4 == 1 时, f(0, n) = f(0, 1) = 1
当 n % 4 == 3 时, f(0, n) = f(0, 3) = 0
以下是打表的程序以及打表的结果:

#include <bits/stdc++.h> using namespace std; int work(int i,int j) { int ans=0; for (int k=1; k<=pow(i,j); k++) ans^=k; return ans; } void en(int i,int j) { printf ("f(%d,%d)=%d ",i,j,work(i,j)); } int main() { int n; n=11; int ans=0; for (int i=1; i<=n; i+=2){ for (int j=1; j<=5; j++){ en(i,j); } printf (" "); } return 0; } /* f(1,1)=1 f(1,2)=1 f(1,3)=1 f(1,4)=1 f(1,5)=1 f(3,1)=0 f(3,2)=1 f(3,3)=0 f(3,4)=1 f(3,5)=0 f(5,1)=1 f(5,2)=1 f(5,3)=1 f(5,4)=1 f(5,5)=1 f(7,1)=0 f(7,2)=1 f(7,3)=0 f(7,4)=1 f(7,5)=0 f(9,1)=1 f(9,2)=1 f(9,3)=1 f(9,4)=1 f(9,5)=1 f(11,1)=0 f(11,2)=1 f(11,3)=0 f(11,4)=1 f(11,5)=0 */
以下是AC代码:
#include <bits/stdc++.h> using namespace std; const int mod=1e9+7; int main() { int n,x,y; scanf ("%d%d%d",&n,&x,&y); int ans=0; int mark=0; for (int i=1; i<=n; i+=2){ if (!mark) ans=(ans+y-x+1)%mod; else ans=(ans+y/2-(x-1)/2)%mod; mark^=1; } printf ("%d ",ans); return 0; }
