动态规划理解

看了知乎用户徐凯强 Andy与王勐回答动态规划提问感觉受益匪浅。在这写下自己理解。

首先要明确，动态规划的本质是找到合适的状态的定义与找到状态转移方程。递归与递推只是实现动态规划的工具。动态规划是思想，递推与递归只是方法。不能本末倒置。

什么是状态与状态转移方程两个人的文章已经进行了详细的说明。简单来说，对于一个问题，如果你想使用动态规划来解决那么必须找到DP方程。而且你定义这个DP方程必须无后效性。找到DP方程后，通过DP方程就可以使用递归或者递推方法解决。

找DP方程是解决动态规划问题的核心。

王勐的总结很好

每个阶段只有一个状态->递推；
每个阶段的最优状态都是由上一个阶段的最优状态得到的->贪心；
每个阶段的最优状态是由之前所有阶段的状态的组合得到的->搜索；
每个阶段的最优状态可以从之前某个阶段的某个或某些状态直接得到而不管之前这个状态是如何得到的->动态规划。

 

拿动态规划的经典问题01背包举例，这里只讲为什么01背包是动态规划问题，而不说01背包的的DP方程是怎么来的。网上有很多很好的推理。

问题的表述如下

0-1 背包问题：给定 n 种物品和一个容量为 C 的背包，物品 i 的重量是 wi，其价值为 vi 。

问：应该如何选择装入背包的物品，使得装入背包中的物品的总价值最大？

如果背包物品可以部分放入，那么这个问题变成了贪心问题。动态规划的一种特殊情况。每次只讲性价比较高的物品放入即可。

对于0-1背包问题这里有两种思路：

1.暴力枚举：尝试将每件物品放入背包中，直到背包容量不足。计算当前组合的价值。最后找到所有组合的最大值。这里用到的便是搜索，当前阶段需要之前所有阶段的状态组合。

2.动态规划：当前背包状态下的最大价值等于，MAX（i-1个包容量为j时计算出最大价值，v(i) +（i-1个包容量为j-w(i)时计算的最大价值））。即求两者的最大值，求当前问题用到了子问题。且两个问题解决方法相同。

暴力枚举代码：

/*测试结果10 
3 6
1 3 5
4 3 6
*/ 
#include<stdio.h>
int flag[100] = {0}; 
int n,c;//数量，容量 
int w[100],v[100];//重量，价值 
int max = 0;//最大价值
int b[100] = {0}; 
int num = 0; 
void f(int weight,int val);
int main(){
    scanf("%d %d",&n,&c);
    for(int i=0;i<n;i++){
        scanf("%d",&w[i]);
    }
    for(int i=0;i<n;i++){
        scanf("%d",&v[i]);
    }
    f(0,0);
    printf("最大价值为：%d
",max);
}
void f(int weight,int val){
    for(int i=0;i<n;i++){
        if(flag[i]==0){            
            if(weight+w[i]<=c){
                flag[i] = 1;
                f(weight+w[i],val+v[i]);
                flag[i] = 0;
            }else{
                max = max>val?max:val;
            }        
        }
    }
} 

测试结果：

3 6
1 3 5
4 3 6

对于动态规划：

首先定义状态：方法f(i,j)或者矩阵a[i][i]表示前i个包（阶段）容量为j时（状态）计算出最大价值。

状态转移方程：f(i,j) = max(a[i-1][j],v[i]+f(i-1,j-w[i]))。

找到状态转移方程就可以解决动态规划问题，可以使用递归也可以使用递推：

递归代码：

#include<stdio.h>
/*测试结果44 
4 20
8 7 6 4
14 15 20 9
*/
int n,c;//数量，容量 
int w[100],v[100];//重量，价值 
int max = 0;//最大价值
int a[100][100]= {0}; 
int f(int i,int j);
//int num = 0;
int main(){
    scanf("%d %d",&n,&c);
    for(int i=1;i<=n;i++){
        scanf("%d",&w[i]);
    }
    for(int i=1;i<=n;i++){
        scanf("%d",&v[i]);
    }
    max = f(n,c);
    printf("%d
",max);
    //printf("递归调用%d次
",num); 
    printf("递归记录矩阵：
");
    for(int i=0;i<c;i++){
        if(i==0) printf("   ");
        printf("%3d",i+1);
    }
    printf("
");
    for(int i=1;i<=n;i++){
        for(int j = 1;j<=c;j++){
            if(j==1) printf("%3d",i);
            printf("%3d",a[i][j]);
        }
        printf("
");
    }
}
int f(int i,int j){
    //num++;
    if(j-w[i]<0){
        return f(i-1,j);
    }else if(i==1){
        a[i][j] = v[1];
        return v[1];
    }else if(i==0){
        return 0;
    }
    int num1,num2;
    if(a[i-1][j]!=0) num1=a[i-1][j];    
    else num1 = f(i-1,j);
    if(a[i-1][j-w[i]]!=0) num2=a[i-1][j-w[i]];
    else num2 = v[i]+f(i-1,j-w[i]);
    a[i][j] = num1>num2?num1:num2;
    return a[i][j];    
} 

递推代码

/*测试结果10 
3 6
1 3 5
4 3 6
*/ 
#include<stdio.h>
int n,c;//数量，容量 
int w[100],v[100];//重量，价值 
int a[100][100]= {0};
int main(){
     scanf("%d %d",&n,&c);
    for(int i=1;i<=n;i++){
        scanf("%d",&w[i]);
    }
    for(int i=1;i<=n;i++){
        scanf("%d",&v[i]);
    }
    for(int i=1;i<=n;i++){
        for(int j=1;j<=c;j++){
            if(j-w[i]>=0)
                a[i][j] = a[i-1][j]>v[i]+a[i-1][j-w[i]]?a[i-1][j]:v[i]+a[i-1][j-w[i]];
            else
                a[i][j] = a[i-1][j];
        }
    }
    printf("%d
",a[n][c]);
    printf("递推记录矩阵：
");
    for(int i=0;i<c;i++){
        if(i==0) printf("   ");
        printf("%3d",i+1);
    }
    printf("
");
    for(int i=1;i<=n;i++){
        for(int j = 1;j<=c;j++){
            if(j==1) printf("%3d",i);
            printf("%3d",a[i][j]);
        }
        printf("
");
    } 
    
} 

测试结果：

对于测试用例

3 6
1 3 5
4 3 6

 

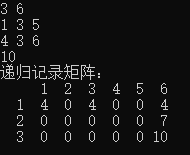
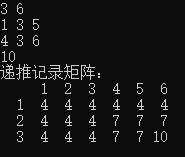
可以看出两种方法本质上是一样，递推记录了每一种容量状态，递归记录了需要的容量状态。

总结：

1. 动态规划的本质是对问题状态的定义和状态转移方程的定义。
2. 找状态转移方程需用到分治的思想，找到最优子结构。
3. 找到状态转移方程便可以使用递归或者递推方法解决问题。