梯度

1. 梯度

梯度的本质：梯度是方向导数最大值的反方向，因此梯度是函数值下降最快的方向。

在谈梯度之前我们需要先了解导数，跟方向导数的概念

1.1 导数

导数大家都很熟悉，即某个点在函数上的变化率。这个点不止是一元函数上的点，即只有一个变量。也有可能是二元，三元函数上的点不止一个自变量。但都表示某个点的在函数上的变化率。比如下面分别表示一元函数导数跟二元函数导数。

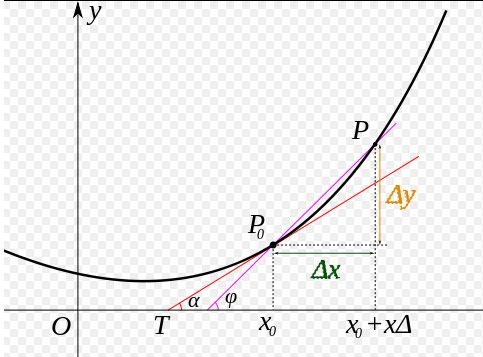
对于一元函数，导数是一条切线

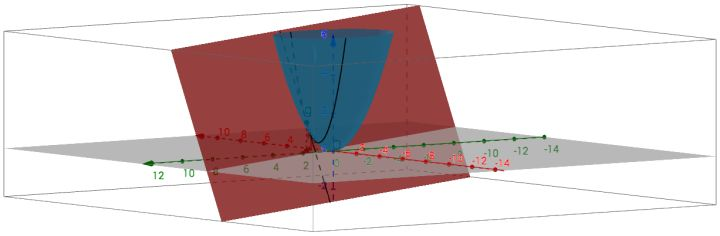
对于二元函数，导数是一个切面

1.2 方向导数

对于二元函数我们在一个点((x,y))上可以做出无数条曲线，如上图我们在Q点每个方向上都可以做出曲线，每条曲线上我们都可以求出Q点在这条曲线上的斜率，如果曲线方向刚好是(x轴,y轴)，那我们求出Q点在这两个方向的斜率就是偏导数。

我们把每个点在不同方向上的导数称为方向导数

下面是方向导数的公式,其中( heta)为方向向量与(x)轴正方向上的夹角

(D_uf(x,y)=f_x(x,y)cos heta+f_y(x,y)sin heta)

1.3 梯度

知道什么是方向导数后想一个问题，Q点在那个方向变化最大呢。在哪个点变化最大就是求方向导数在什么时候最大，因为方向导数代表了点在各个方向上的变化率。

我们把方向导数写成向量点成的形式就是

(D_uf(x,y)=(f_x(x,y),f_y(x,y))cdot（cos heta,sin heta）)

(因此D_uf(x,y)=|(f_x(x,y),f_y(x,y))| |cos heta,sin heta|cosalpha)

(|cos heta,sin heta|)的长度为1，当(alpha)等于0的时候方向导数最大，最大为(|(f_x(x,y),f_y(x,y))|),有没有发现这个值刚好梯度的负值。因此我们说梯度为方向导数最大值的反方向，沿梯度方向函数值下降最快。

2. 参考

1. 求解全微分的意义？最好感性一点的认识 - 马同学的回答 - 知乎
   https://www.zhihu.com/question/31464934/answer/152231899
2. 如何直观形象的理解方向导数与梯度以及它们之间的关系？ - 忆臻的回答 - 知乎
   https://www.zhihu.com/question/36301367/answer/142096153