国内博客,上介绍实现的K-medodis方法为:
与K-means算法类似。只是距离选择与聚类中心选择不同。
距离为曼哈顿距离
聚类中心选择为:依次把一个聚类中的每一个点当作当前类的聚类中心,求出代价值最小的点当作当前聚类中心。
维基百科上,实现的方法为PAM算法。
分成K类,把每个点都尝试当作聚类中心,并求出当前组合聚类中心点组合的代价值。找到总最小代价值的中心点。
国内实现:
kMedoids.m代码:
function [cx,cost] = kMedoids(K,data,num) % 生成将data聚成K类的最佳聚类 % K为聚类数目,data为数据集,num为随机初始化次数 [cx,cost] = kMedoids1(K,data); for i = 2:num [cx1,min] = kMedoids1(K,data); if min<cost cost = min; cx = cx1; end end end function [cx,cost] = kMedoids1(K,data) % 把分类数据集data聚成K类 % [cx,cost] = kmeans(K,data) % K为聚类数目,data为数据集 % cx为样本所属聚类,cost为此聚类的代价值 % 选择需要聚类的数目 % 随机选择聚类中心 centroids = data(randperm(size(data,1),K),:); % 迭代聚类 centroids_temp = zeros(size(centroids)); num = 0; while (~isequal(centroids_temp,centroids)&&num<20) centroids_temp = centroids; [cx,cost] = findClosest(data,centroids,K); centroids = compueCentroids(data,cx,K); num = num+1; end % cost = cost/size(data,1); end function [cx,cost] = findClosest(data,centroids,K) % 将样本划分到最近的聚类中心 cost = 0; n = size(data,1); cx = zeros(n,1); for i = 1:n % 曼哈顿距离 [M,I] = min(sum(abs((data(i,:)-centroids))')); cx(i) = I; cost = cost+M; end end function centroids = compueCentroids(data,cx,K) % 计算新的聚类中心 centroids = zeros(K,size(data,2)); for i = 1:K % 寻找代价值最小的当前聚类中心 temp = data((cx==i),:); [~,I] = min(sum(squareform(pdist(temp)))); centroids(i,:) = temp(I,:); end end
Main.m
% 主函数 % 生成符合高斯分布的数据 mu = [5,5]; sigma = [16,0;0,16]; sigma1 = [0.5,0;0,0.5]; data = gaussianSample(8,50,mu,sigma,sigma1); % 聚类 K = 6; [cx,cost] = kMedoids(K,data,10); plotMedoids(data,cx,K);
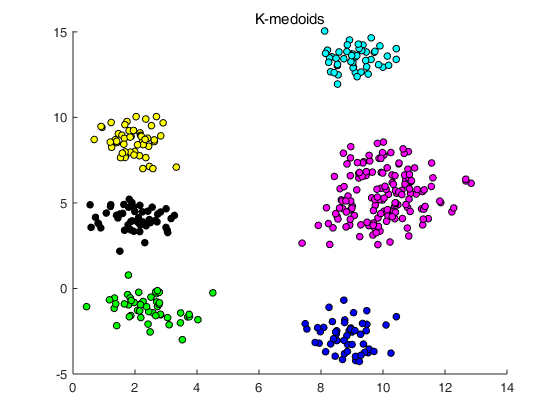
执行Main.m结果为: