K-means聚类算法MATLAB

以K-means算法为例，实现了如下功能

1. 自动生成符合高斯分布的数据，函数名为gaussianSample.m
2. 实现多次随机初始化聚类中心，以找到指定聚类数目的最优聚类。函数名myKmeans.m
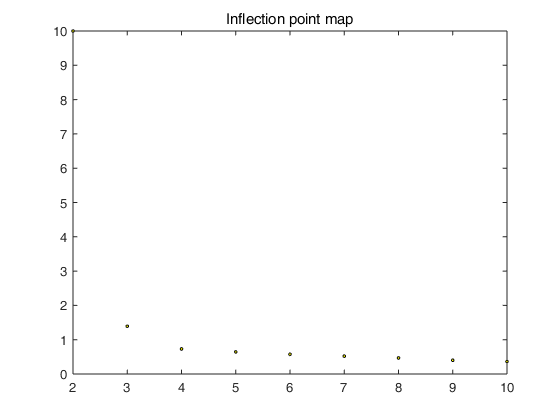
3. 自动寻找最佳聚类数目，函数名称besKmeans.m，并绘制了拐点图（L图）

gaussianSample.m

function [data] = gaussianSample(n,m,mu,sigma,sigma1)
%   生成n个符合多元高斯分布的样本
%   data = gaussianSample(n,m,mu,sigma,mu1,sigma1)
%   生成一个符合高斯分布的数据集data
%   n表示生成的数量，m表示每个簇的点的数量
%   先通过mu与sigma生成簇中心的分布情况
%   在通过簇中心分布mu1与sigma1生成每个簇的的分布情况
%   mu与mu1为均值，sigma与sigma1为协方差矩阵。


% % 默认值生成2维数据
% m = 100;
% mu = [5,5];
% sigma = [16 0;0 16];
% sigma1 = [0.5,0;0,0.5];

% 生成中心点分布
mu1 =  mvnrnd(mu,sigma,n);
% 生成数据
data = [];
for i = 1:n
    temp = mvnrnd(mu1(i,:),sigma1,m);
    data = [data;temp];
end

% % 可视化样本,以二维数据为例
% hold on;
% plot(data(:,1),data(:,2),'ko','MarkerFaceColor','y');
% plot(mu1(:,1),mu1(:,2),'r+','LineWidth',2,'MarkerSize',7);
% hold off;

myKmeans.m

function [cx,cost] = myKmeans(K,data,num)
% 生成将data聚成K类的最佳聚类
    [cx,cost] = kmeans1(K,data);
    for i = 2:num
        [cx1,min] = kmeans1(K,data);
        if min<cost
            cost = min;
            cx = cx1;
        end
    end
%     plotMeans(data,cx,K); 
end

function [cx,cost] = kmeans1(K,data)
%KMEANS 把数据集data聚成K类
%   [cx,cost] = kmeans(K,data)
%   K为聚类数目，data为数据集
%   cx为样本所属聚类，cost为此聚类的代价值
% 选择需要聚类的数目

% 随机选择聚类中心
    centroids = data(randperm(size(data,1),K),:);
% 迭代聚类 
    centroids_temp = zeros(size(centroids));
    num = 0;
    while (~isequal(centroids_temp,centroids)&&num<20)
        centroids_temp = centroids;
        [cx,cost] = findClosest(data,centroids,K);
        centroids = compueCentroids(data,cx,K);
        num = num+1;
    end
    cost = cost/size(data,1);

end

function [cx,cost] = findClosest(data,centroids,K)
% 将样本划分到最近的聚类中心
    cost = 0;
    n = size(data,1);
    cx = zeros(n,1);
    for i = 1:n
        [M,I] = min(sum((centroids-data(i,:))'.^2));
        cx(i) = I;
        cost = cost+M;
    end
  
end



function centroids = compueCentroids(data,cx,K)
% 计算新的聚类中心
    centroids = zeros(K,size(data,2));
    for i = 1:K
        centroids(i,:) = mean(data(cx==i,:));
    end
end

bestKmeans.m

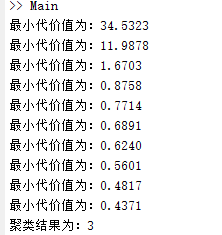
function [num,cx] = bestKmeans(data,m,n)
%   返回数据集的最佳聚类数目与聚类结果
%   data为数据集，m为寻找的最大聚类数量，n为每次聚类寻找次数
%   返回num最佳聚类数量，cx聚类结果。
costs = zeros(m,1)';
for i = 1:m
    [~,cost] = myKmeans(i,data,n);
    costs(i) = cost;
    fprintf('最小代价值为：%.4f
',cost);
end
 costs = costs./costs(2)*m;
 % 绘制拐点图
X = (1:m)';
X = [X,costs'];

plot(X(2:m,1),X(2:m,2),'ko','MarkerFaceColor','y','MarkerSize',2);
title('Inflection point map');
% 寻找最佳聚类
min = -1;
for i = 3:m
    x1 = X(2,:)-X(i,:);
    x2 = X(m,:)-X(i,:);
    k = x1*x2'/((x1*x1')*(x2*x2'));
    if k>min&&k<0
        num = i;
        min = k;
    end
end
% fprintf('聚类结果为：%d
',num);
[cx,~] = myKmeans(num,data,n);
end

plotMeans.m

function [] = plotMeans(data,cx,K)
% 可视化数据聚类效果
    figure;
    color='cbygmkr';
    hold on;
    for i = 1:K
        px = find(cx==i);
        plot(data(px,1),data(px,2),'ko','MarkerFaceColor',color(i),'MarkerSize',5);
    end
    title('K-means')
    hold off;
end

Main.m

% 主函数

% 生成符合高斯分布的数据
mu = [5,5];
sigma = [16,0;0,16];
sigma1 = [0.5,0;0,0.5];
data =  gaussianSample(4,50,mu,sigma,sigma1);

% 计算最佳聚类数量与结果
[num,cx] = bestKmeans(data,10,10);
fprintf('聚类结果为：%d
',num);
plotMeans(data,cx,num);

执行Main.m代码，自动检测最佳聚类数目。结果如图