对于网格图,尤其是这种要求相邻各自不同的,考虑黑白染色
对于这张染色后图来说:
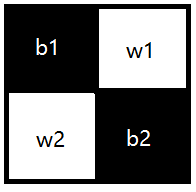
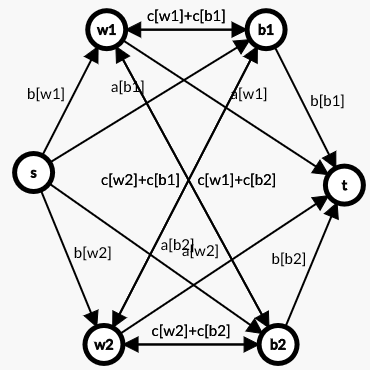
对于每个黑格:
- 表示初始时选择商业区;
- s点向它连商业区收益的流量,它向t点连工业区收益的流量;
- 割断S侧的边说明反悔,则保留T侧边的边权(工业区),割断T侧的边说明维持原样,保留S侧边权(商业区)
对于每个白格:
- 表示初始时选择工业区;
- s点向它连工业区收益的流量,它向t点连商业区收益的流量;
- 割断S侧的边说明反悔,则保留T侧边的边权(商业区),割断T侧的边说明维持原样,保留S侧边权(工业区)
对于相邻格子:
- 相邻黑白格子间连区域不同收益的流量,双向边(注意是这两个格子的c值和)
- 如果相邻两个点被划入同侧,则它们中间的边不会被割,收益被保留;如果被划入异侧,则中间边被割断,收益被减掉
(ans = sum- 最小割) (注意这里的sum是对于每个周边有k个格子的格子(i,j),算上c[i][j]*k)
建图:
#include<iostream>
#include<cstdio>
#include<queue>
#include<cstring>
using namespace std;
const int N=105,E=1000005,inf=1e9,dx[]={1,-1,0,0},dy[]={0,0,-1,1};
int n,m,a[N][N],b[N][N],c[N][N],id[N][N],s,t,sum,h[E],cnt=1,le[E];
struct qwe
{
int ne,to,va;
}e[E<<1];
int read()
{
int r=0,f=1;
char p=getchar();
while(p>'9'||p<'0')
{
if(p=='-')
f=-1;
p=getchar();
}
while(p>='0'&&p<='9')
{
r=r*10+p-48;
p=getchar();
}
return r*f;
}
void add(int u,int v,int w)
{
cnt++;
e[cnt].ne=h[u];
e[cnt].to=v;
e[cnt].va=w;
h[u]=cnt;
}
void ins(int u,int v,int w)
{
add(u,v,w);
add(v,u,0);
}
bool bfs()
{
queue<int>q;
memset(le,0,sizeof(le));
le[s]=1;
q.push(s);
while(!q.empty())
{
int u=q.front();
q.pop();
for(int i=h[u];i;i=e[i].ne)
if(!le[e[i].to]&&e[i].va>0)
{
le[e[i].to]=le[u]+1;
q.push(e[i].to);
}
}
return le[t];
}
int dfs(int u,int f)
{
if(u==t||!f)
return f;
int us=0;
for(int i=h[u];i&&us<f;i=e[i].ne)
if(le[u]+1==le[e[i].to]&&e[i].va>0)
{
int t=dfs(e[i].to,min(e[i].va,f-us));
e[i].va-=t;
e[i^1].va+=t;
us+=t;
}
if(!us)
le[u]=0;
return us;
}
int dinic()
{
int re=0;
while(bfs())
re+=dfs(s,inf);
return re;
}
int main()
{
n=read(),m=read();
t=n*m+1;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
a[i][j]=read(),sum+=a[i][j];
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
b[i][j]=read(),sum+=b[i][j];
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
{
c[i][j]=read();
int t=0;
for(int k=0;k<4;k++)
if(i+dx[k]>=1&&i+dx[k]<=n&&j+dy[k]>=1&&j+dy[k]<=m)
t++;
sum+=c[i][j]*t;
}
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
id[i][j]=(i-1)*m+j;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
{
if((i+j)%2==1)
{
ins(s,id[i][j],a[i][j]);
ins(id[i][j],t,b[i][j]);
}
else
{
ins(s,id[i][j],b[i][j]);
ins(id[i][j],t,a[i][j]);
}
// for(int k=0;k<4;k++)
// if(i+dx[k]>=1&&i+dx[k]<=n&&j+dy[k]>=1&&j+dy[k]<=m)
// ins(id[i][j],id[i+dx[k]][j+dy[k]],c[i][j]+c[i+dx[k]][j+dy[k]]);
if(i!=n)
{
add(id[i][j],id[i+1][j],c[i][j]+c[i+1][j]);
add(id[i+1][j],id[i][j],c[i][j]+c[i+1][j]);
}
if(j!=m)
{
add(id[i][j],id[i][j+1],c[i][j]+c[i][j+1]);
add(id[i][j+1],id[i][j],c[i][j]+c[i][j+1]);
}
}
printf("%d
",sum-dinic());
return 0;
}