前一篇介绍了一种最小生成树的算法--Kruskal算法,本篇介绍另一种Prim算法
算法描述
定义V为端点的集合,A为最小生成树,初始为空。对于每个端点v初始的Key[v]=∞, Parent[v]=null
初始化Q为V, 指定任意一个端点为root,其值Key[r]=0
while(Q不为空) {
找出Q中Key值最小的u
Q = Q - u
if (PARENT[u] != null) {
将(u, Parent(u))加入A中
}
foreach(u的相邻端点v) {
if (v在Q中且w(u, v) < Key[v]) {
PARENT[v] = u;
Key[v] = w;
}
}
return A
图片示例
初始状态
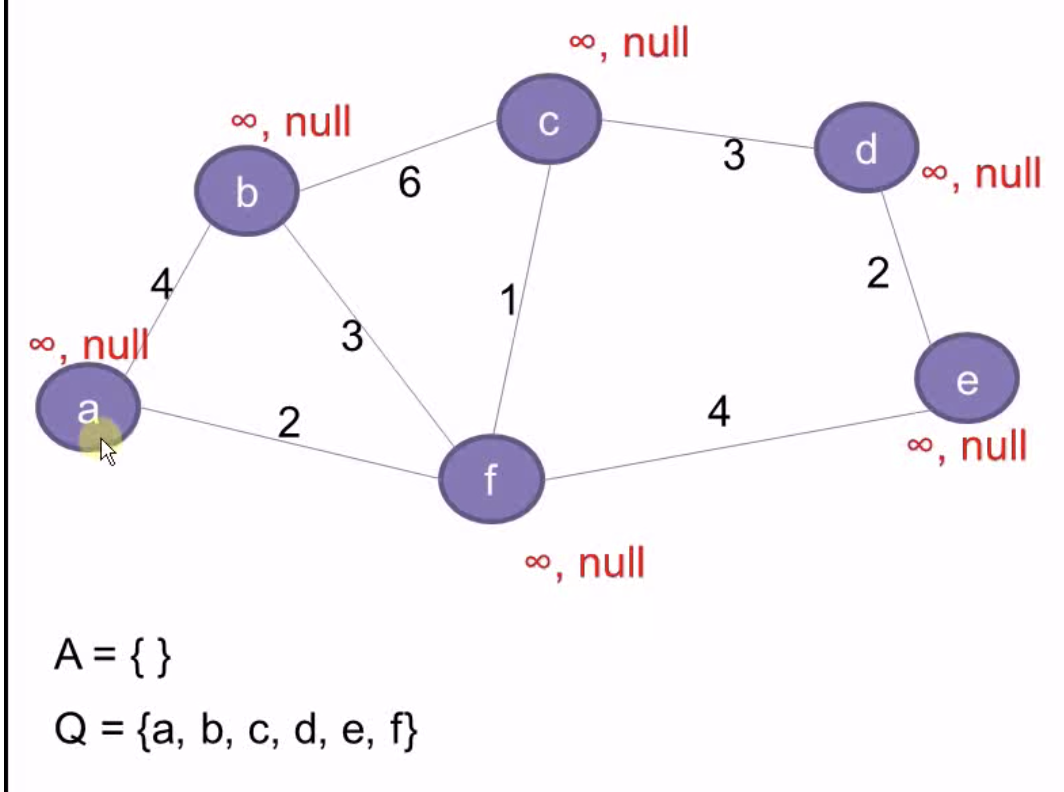
选择一个端点a作为root

找出Q中Key最小的a,将其从Q中删除,同时更新其相邻端点b和f的Key和PARENT
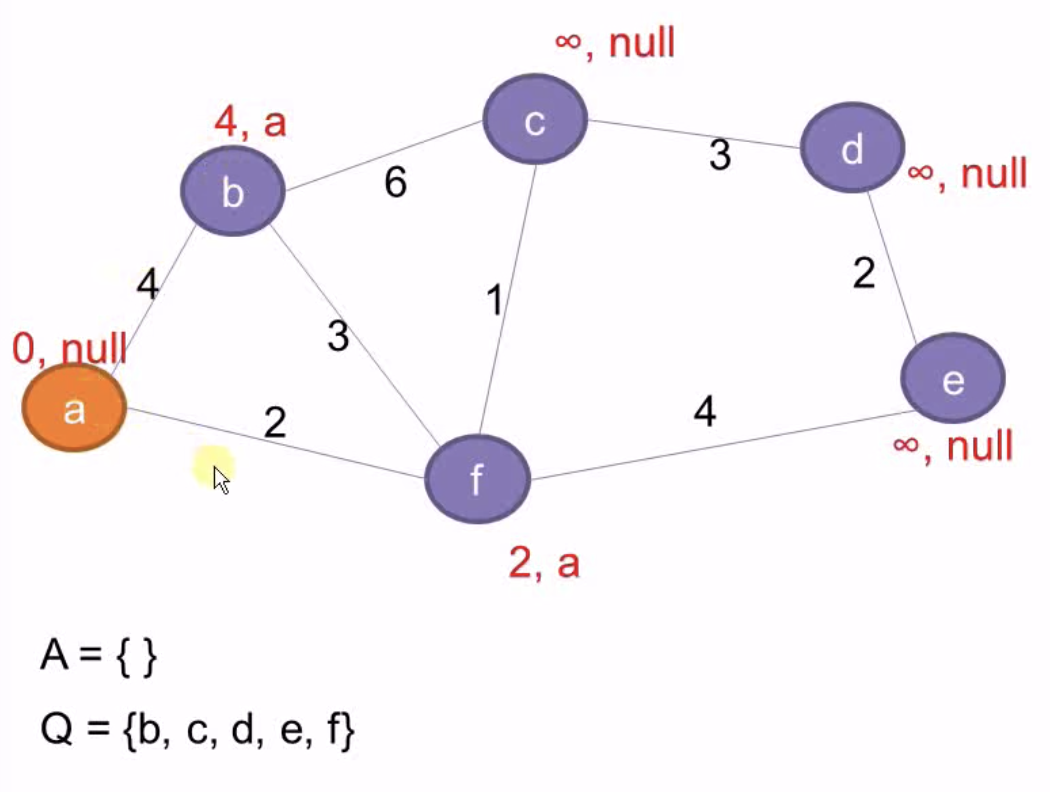
找出Q中Key最小的f, 从Q中删除,因为f的父节点为a,将(a, f)加到A中。同时更新f相邻节点的Key和父节点
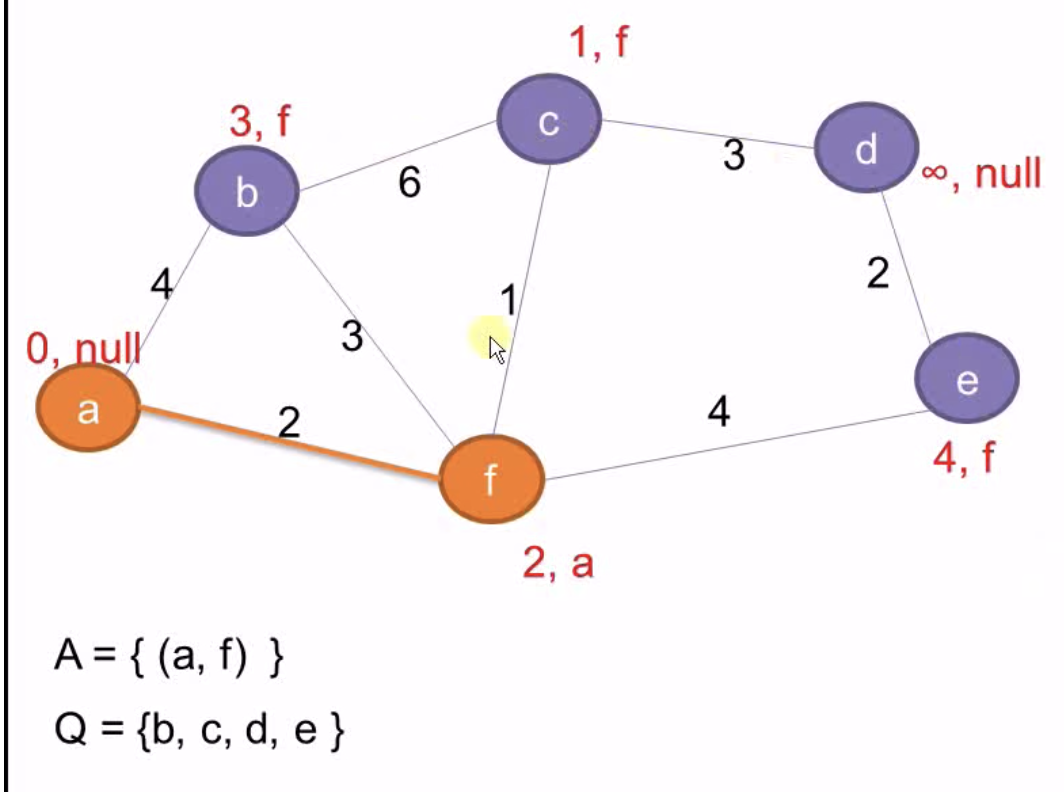
Q减去c,A加上(c ,f), 更新相邻节点d的Key和父节点
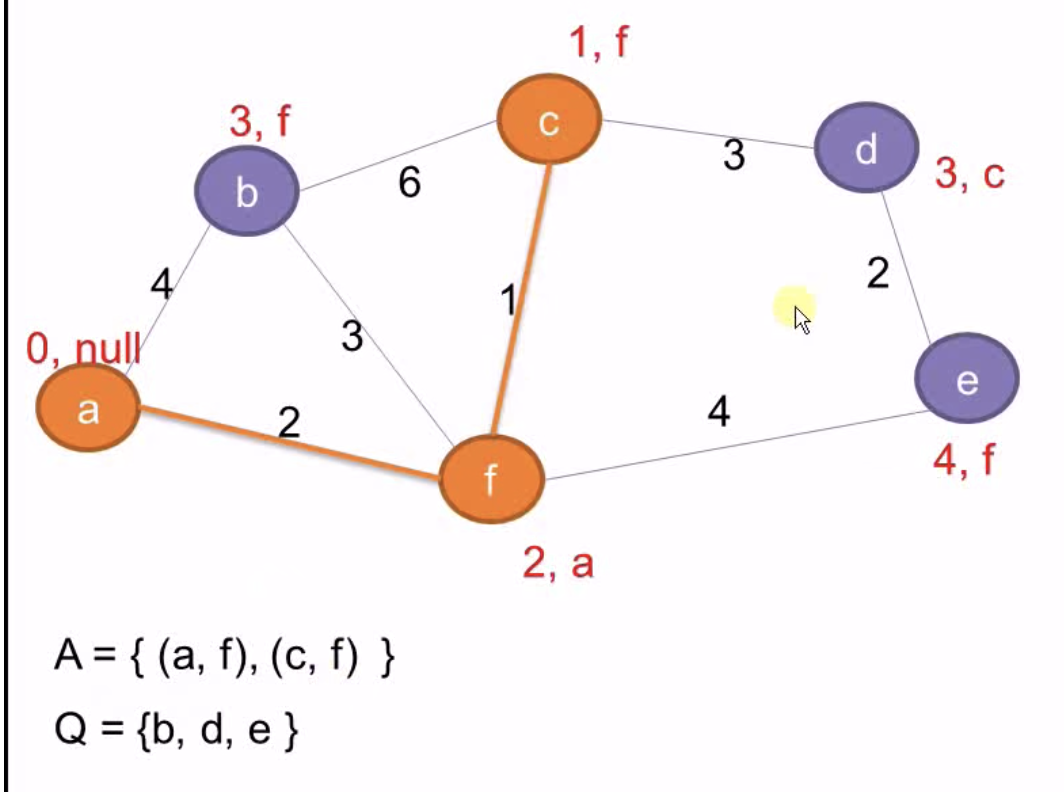
Q减去b,A加上(b, f)

Q减d,A加(c, d)
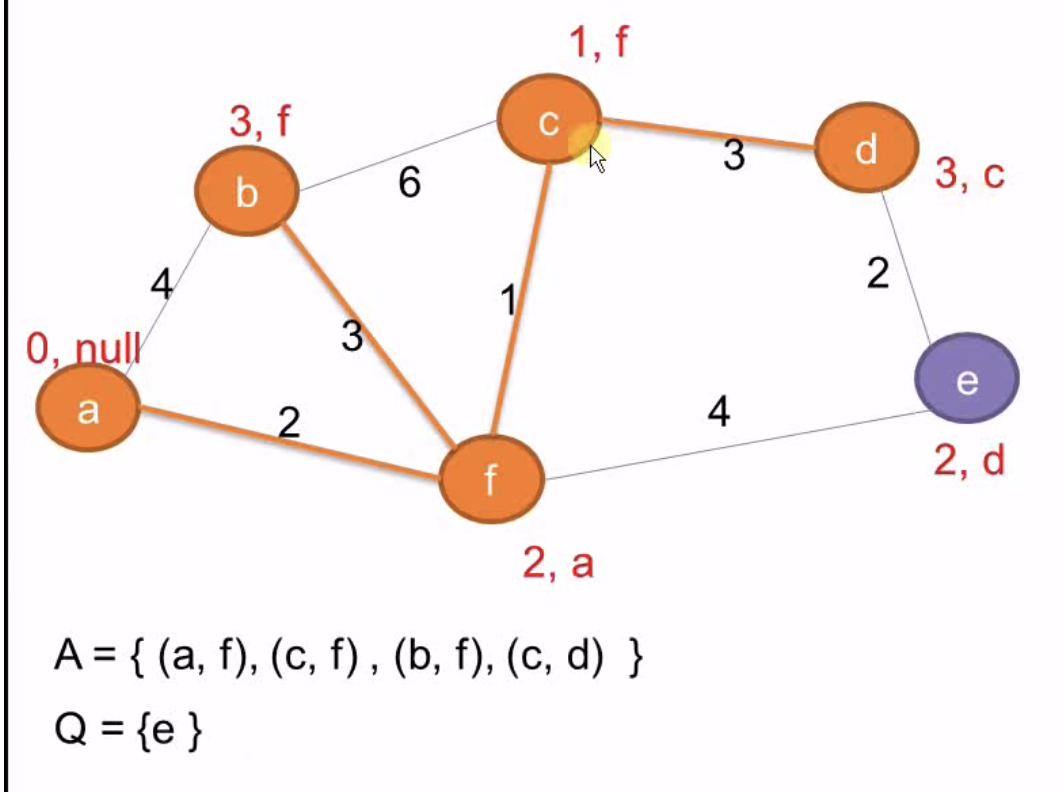
Q减e,A加(d, e)
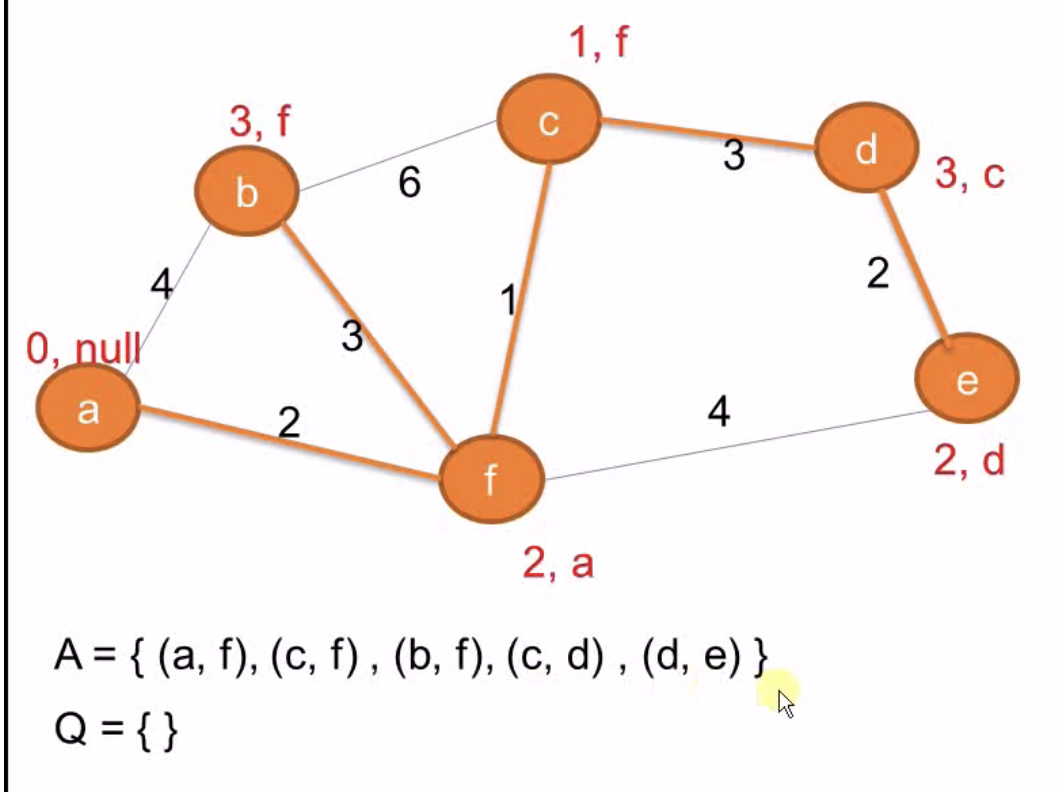
C++代码实现
struct Edge { char vertex1; char vertex2; int weight; Edge(char v1, char v2, int w):vertex1(v1), vertex2(v2), weight(w) {} }; struct Graph { vector<char> vertice; vector<Edge> edges; vector< pair<char, Edge> > adjacent(char u) { // 返回端点u所有相邻的端点及权重 vector< pair<char, Edge> > res; for (Edge e : edges) { if (e.vertex1 == u) { res.push_back( make_pair(e.vertex2, e)); } else if (e.vertex2 == u) { res.push_back( make_pair(e.vertex1, e)); } } return res; } }; void prim(Graph& g, char root) { unordered_map<char, char> res; unordered_map<char, char> PARENT; unordered_map<char, int> KEY; for (auto c : g.vertice) { PARENT[c] = '�'; KEY[c] = INT_MAX; } KEY[root] = 0; vector<char> Q = g.vertice; while (!Q.empty()) { // O(V) char u = *std::min_element(Q.begin(), Q.end(), [&](char x, char y) {return KEY[x] < KEY[y];}); // O(v) vector<char>::iterator itr = remove(Q.begin(), Q.end(), u); // O(V) Q.erase(itr, Q.end()); // erase() following remove() idiom if (PARENT[u] != '�') { res[u] = PARENT[u]; // This is one edge of MST } vector< pair<char, Edge> > adj = g.adjacent(u); // O(E) for (pair<char, Edge> v : adj) { if (find(Q.begin(), Q.end(), v.first) != Q.end()) { // O(V) if (v.second.weight < KEY[v.first]) { PARENT[v.first] = u; KEY[v.first] = v.second.weight; } } } } for (auto e : res) { cout << e.first << " -- " << e.second << endl; } } int main() { Graph g; char t[] = {'a', 'b', 'c', 'd', 'e', 'f'}; g.vertice = vector<char>(t, t + sizeof(t)/sizeof(t[0])); g.edges.push_back(Edge('a', 'b', 4)); g.edges.push_back(Edge('a', 'f', 2)); g.edges.push_back(Edge('f', 'b', 3)); g.edges.push_back(Edge('c', 'b', 6)); g.edges.push_back(Edge('c', 'f', 1)); g.edges.push_back(Edge('f', 'e', 4)); g.edges.push_back(Edge('d', 'e', 2)); g.edges.push_back(Edge('d', 'c', 3)); prim(g, 'a'); return 0; }