0.PTA得分截图

1.本周学习总结(0-5分)
1.1 总结树及串内容
1.1.1串的BFKMP算法
1.BF(Brute-Force)算法
- +暴力匹配(BF)算法是普通的模式匹配算法,BF算法的思想就是将目标串S的第一个字符与模式串T的第一个字符进行匹配,若相等,则继续逐个比较后续字符;若不相等,则从串S的第二个字符和T的第一个字符,依次比较,直到得出最后的匹配结果
以此类推,直至串t中的每一个字符依次和串s的一个连续的字符序列相等,则称模式匹配成功,此时串t的第一个字符在串s中的位置就是t在s中的位置,否则模式匹配不成功
代码实现
int BF(char* s, char* t)
{
int i = 0, j = 0, countOne = 0, countTwo = 0;
while (s[i] != '�')
{
i++;
countOne++; //变量countOne记录目标串s的长度
}
while (t[j] != '�')
{
j++;
countTwo++; //变量countTwo记录模式串t的长度
}
i = 0, j = 0;
while (i < countOne && j < countTwo)
{
if (s[i] == t[j]) //若相等,继续比较两串的下一字符
{
i++;
j++;
}
else //若不相等,目标串s回溯到下一字符处,模式串t回溯到第一个字符处
{
i = i - j + 1;
j = 0;
}
}
if (j >= countTwo)
{
return i - countTwo;
}
else
{
return -1;
}
}
2.KMP算法
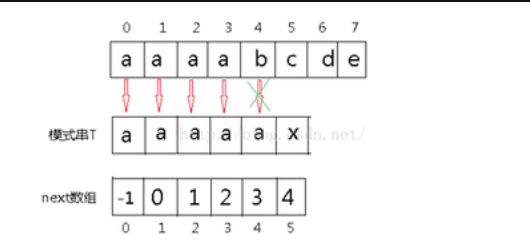
-
BF算法但主串出现多个重复且同时出现在子串时,会多次进行重复的操作,使算法的效率变低,这样我们就对BF算法进行了改进,引进了next数组来辅助操作
-
在KMP算法中,-对于每一个模式串都会事先计算出模式串的内部匹配信息,在匹配失败时最大的移动模式串,以减少匹配次数,这样就很好的解决了-BF算法的缺陷
比如,当匹配失败后,最好是能够将模式字串尽量的右移和主串进行匹配,使程序的效率达到更高,右移的距离在-KMP算法中是这样计算的:在已经匹配的字串中,找到最长的相同的前缀和后缀,然后移动使他们重叠,这个位置就是j要回退的位置,这样j就不用每一次都回到0号位置了,每一次j回退的位置存储在一个数组里,称之为-next数组
代码实现
#include<string.h>
const int MAX_LEN = 20010;
// 递推计算Next数组,模板串为str,模板串长度为len
void get_next(char str[], int len, int next[])
{
int i = 0, j = 0;
next[0] = -1;
for (i = 1; i < len; i++) {
while (j > 0 && str[i] != str[j])
j = next[j-1];
if (str[i] == str[j]) j++;
next[i] = j;
}
}
// 在字符串s中匹配字符串t,s长度为len_s,t长度为len_t,t的Next数组为next[],返回t第一次出现的位置
int find_pattern(char s[], int len_s, char t[], int len_t, int next[])
{
int i = 0, j = 0;
while(i < len_s && j < len_t)
{
//匹配字符
if(j == -1 || s[i] == t[j])
{
j++;
i++;
}
else{
j = next[j];
}
}
if(j == len_t)
return i - j ;
else
return -1;
}
int main()
{
int cas,a;
char s[MAX_LEN], t[MAX_LEN];
int next[MAX_LEN];
scanf("%d", &cas);
while (cas --)
{
scanf("%s %s", s, t);
int len_s = strlen(s);
int len_t = strlen(t);
get_next(t, len_t, next);
a=find_pattern(s, len_s, t, len_t, next);
if(a==-1)
printf("not find!
");
else
printf("%d
", a);
}
return 0;
}
1.2二叉树存储结构、建法、遍历及应用
-
二叉树是树中一种特殊的结构,二叉树的每个节点最多有两个子树,即:左子树和右子树
常见应用
二叉树:

-
二叉树的类别:
-
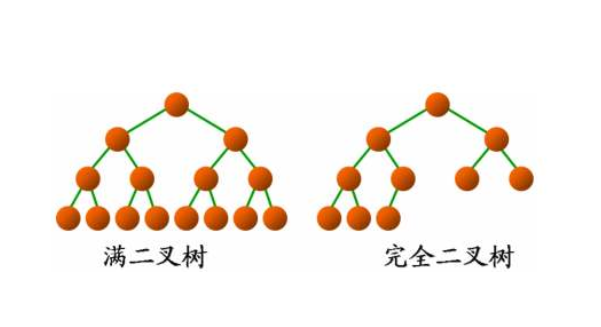
满二叉树:满二叉树属于二叉树的一种,即除了叶子节点之外,每一个节点都有左子树和右子树,且叶子节点都处在最底层的二叉树

-
完全二叉树:满二叉树其实是完全二叉树的一种特殊情形,二叉树从上到下从左到右依次遍历,除了叶子节点之外不会遇到空节点,也就是说,最后一层不一定要满
-
顺序存储结构
#define Maxsize 100
typedef struct TNode {
char tree[Maxsize]; //数组存放二叉树中的节点
int parent; //表示双亲结点的下标
}TNode, * BTree;
-
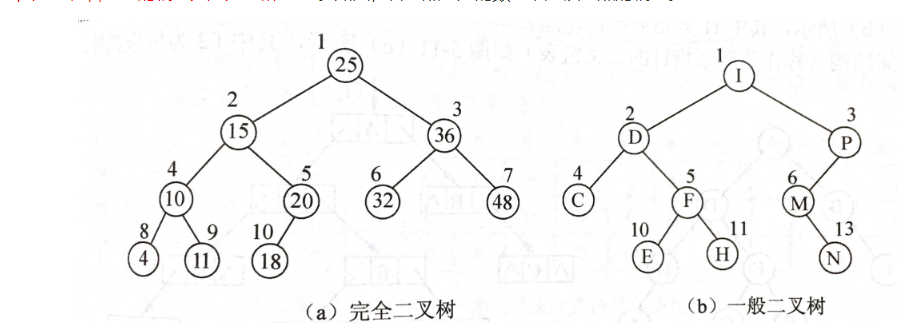
+在二叉树的顺序储存结构当中,节点与节点之间的关系是通过下标来体现的,因此,在顺序储存结构当中,访问双亲节点和左孩子,右孩子节点都是非常方便的。例如:有一编号为i的节点,他的双亲节点的下标为i/2,若存在左孩子和右孩子,则其左孩子的下标为2i,右孩子的下标为2i+1
-
+当我们对完全二叉树进行操作时,利用顺序储存结构是很方便的,但是遇到一般二叉树,就会存在大量储存空间未被利用的情况,因此,我们引进了链式储存结构

-
链式存储结构
不带双亲指针的链式储存结构
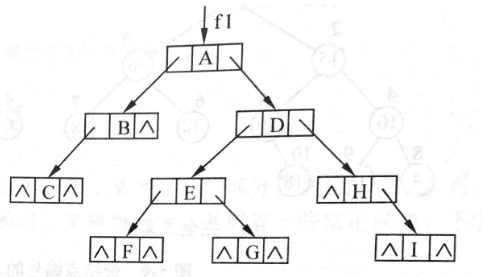
带双亲指针的链式储存结构
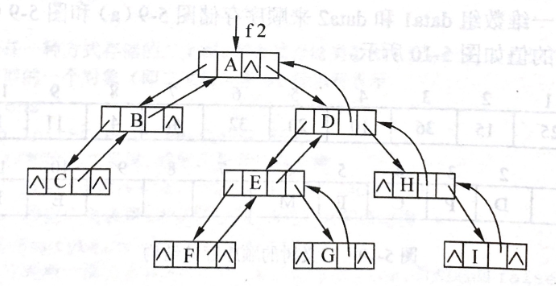
typedef struct TNode { //二叉树结点由数据域,左右指针组成
char data;
struct TNode* lchild;
struct TNode* rchild;
}TNode, * BTree;
二叉树建法
建树函数的参数为字符串
int n = 0; //全局变量n,用于每次调用建树函数时访问字符串中的字符
BTree Create(string str)
{
BTree tree;
if (str[n] == '#') //字符'#'代表空节点
{
n++;
return NULL;
}
else
{
tree = new TNode; //树结构按照树的先序遍历递归建树
tree->data = str[n];
n++;
tree->lchild = Create(str);
tree->rchild = Create(str);
}
return tree;
}
建树函数的参数为字符串和整型变量
{
BTree tree = new TNode; //创建根节点
tree->data = str[i];
if (2 * i > str.length() - 1 || str[2 * i] == '#') //若字符串下标出界或字符为'#',子树为空
{
tree->lchild = NULL;
}
else
{
tree->lchild = Create(str, 2 * i); //递归调用建树函数构建子树
}
if (2 * i + 1 > str.length() - 1 || str[2 * i + 1] == '#')
{
tree->rchild = NULL;
}
else
{
tree->rchild = Create(str, 2 * i + 1);
}
return tree;
}
二叉树遍历
先序遍历(前序遍历):对于当前节点,先输出该节点,然后输出它的左孩子,最后输出它的右孩子
void PreorderTraverse(BinTree BT)
{
if (BT == NULL)
{
return;
}
else
{
cout << BT->data << " ";
PreorderTraverse(BT->Left);
PreorderTraverse(BT->Right);
}
}
中序遍历:对于当前节点,先输出它的左孩子,然后输出该节点,最后输出它的右孩子
void InorderTraverse(BinTree BT)
{
if (BT == NULL)
{
return;
}
else
{
InorderTraverse(BT->Left);
cout << BT->data << " "; //访问根节点
InorderTraverse(BT->Right);
}
}
后序遍历:对于当前节点,先输出它的左孩子,然后输出它的右孩子,最后输出该节点
void PostorderTraverse(BinTree BT)
{
if (BT == NULL)
{
return;
}
else
{
PostorderTraverse(BT->Left);
PostorderTraverse(BT->Right);
cout << BT->data << " "; //访问根节点
}
}
层次遍历:借助队列,逐层地对二叉树从左到右访问所有节点
void level(BTree tree)
{
int flag = 0;
queue<BTree>qu;
qu.push(tree);
while (!qu.empty())
{
if (qu.front()->lchild != NULL)
{
qu.push(qu.front()->lchild);
}
if (qu.front()->rchild != NULL)
{
qu.push(qu.front()->rchild);
}
if (flag == 0) //控制空格的输出
{
cout << qu.front()->data;
flag = 1;
}
else
{
cout << " " << qu.front()->data;
}
qu.pop();
}
return;
}
1.3树的结构、操作、遍历及应用
- 树的结构:
- +1.双亲表示法
typedef struct
{
ElemType data;
int parent;
} Tree;
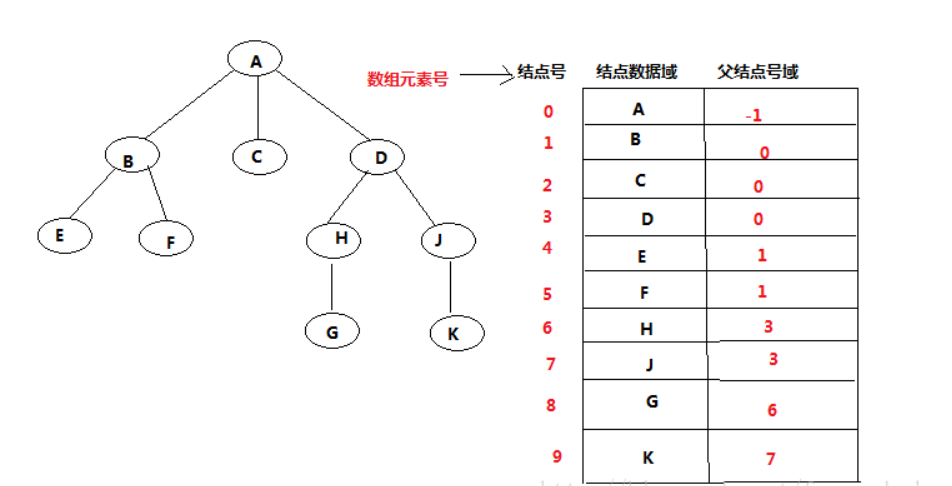
- 2.孩子表示法
typedef struct TSnode
{
ElemType data;
struct TSnode *child[MaxSons];
} TNode;
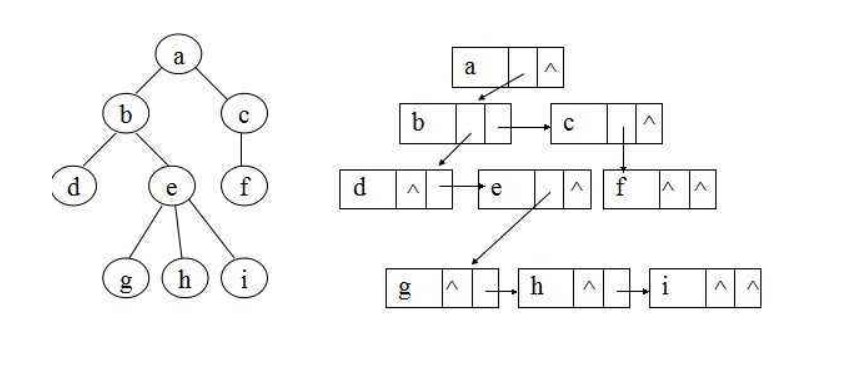
- 3.孩子兄弟链存储结构
typedef struct Tnode
{
ElemType data; //结点的值
struct Tnode *son; //指向兄弟
struct Tnode *brother; //指向孩子结点
} TSBNode;
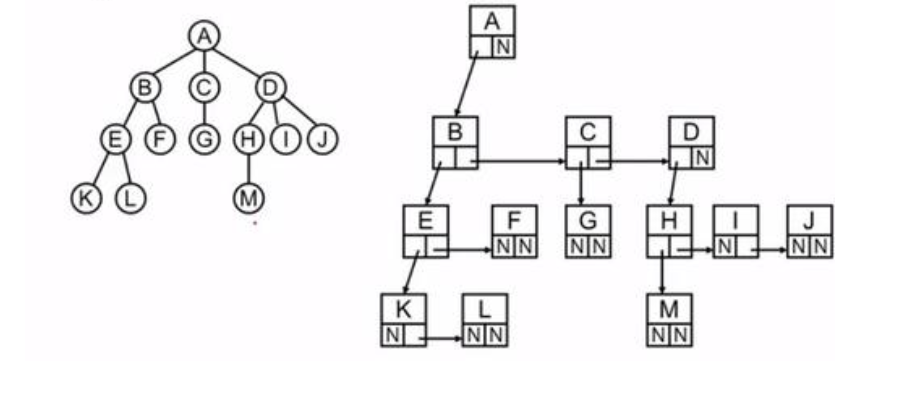
树的遍历
先序遍历
根 左 右:
A. 先 访问根结点
B. 再 先序 访问左子树
C. 后 先序 访问右子树
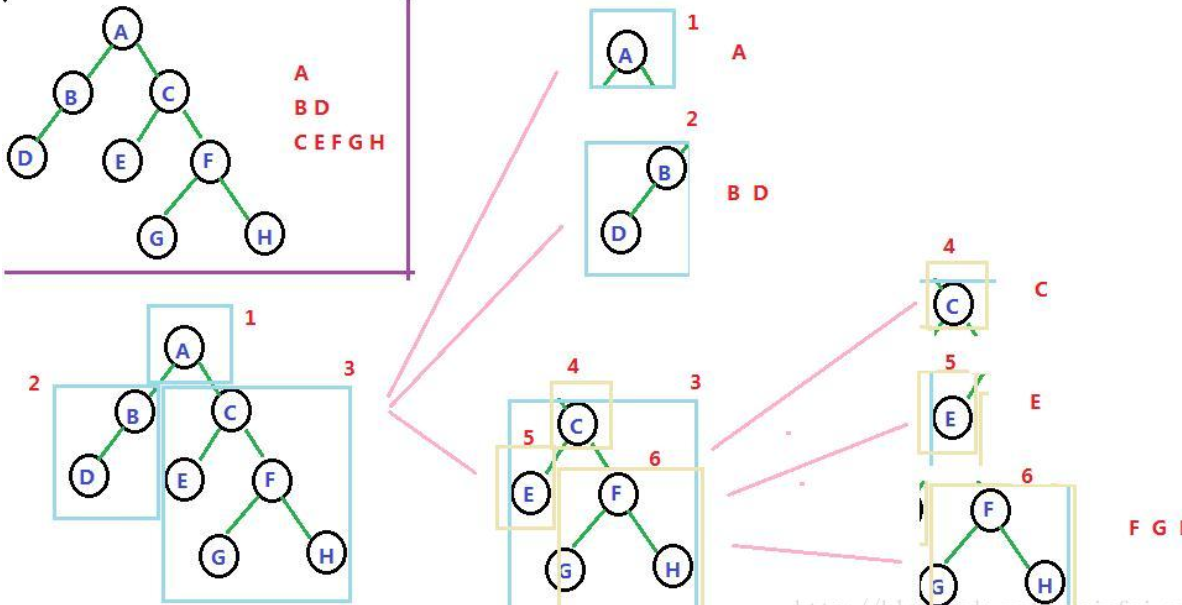
中序遍历
左 根 右

后序遍历
左 右 根
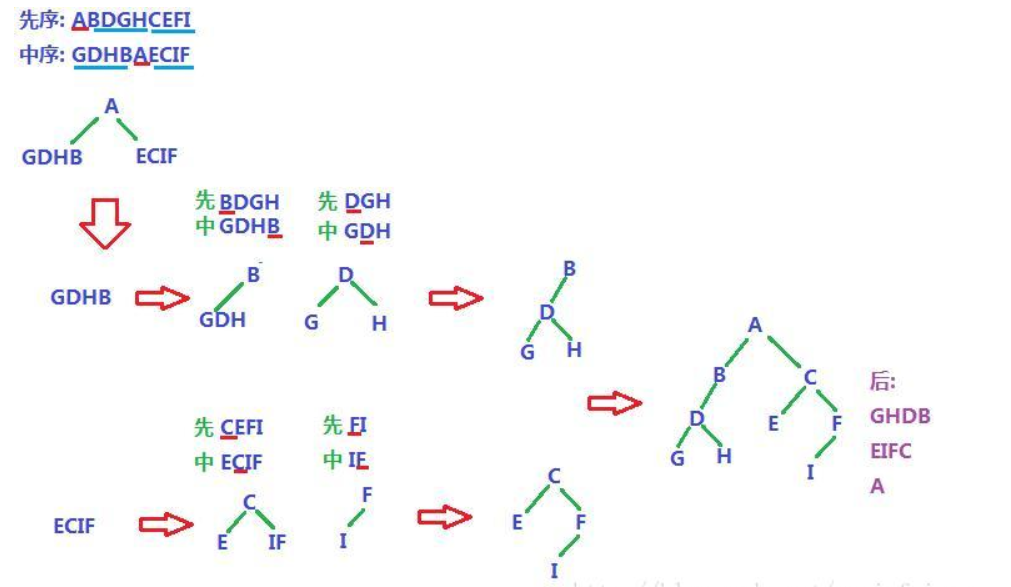
已知 先序 和 中序
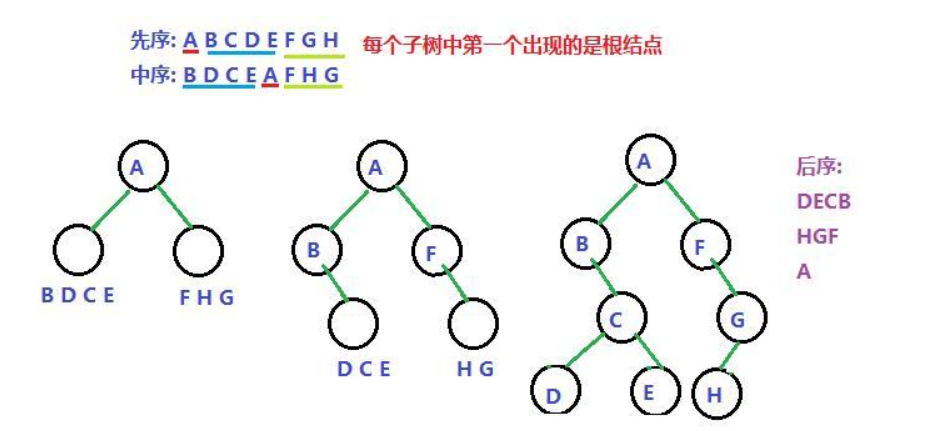
已知 后序 和 中序

-
树的应用
-
+打开文件夹时,若要出现多个子文件夹,使用的存储结构就是树结构
-
+QQ联系人的分类中,同一类联系人放到同一目录下,使用的存储结构就是树结构
线索二叉树

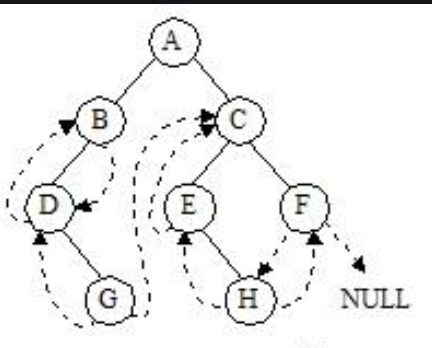
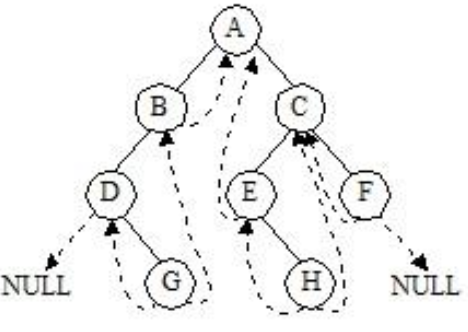
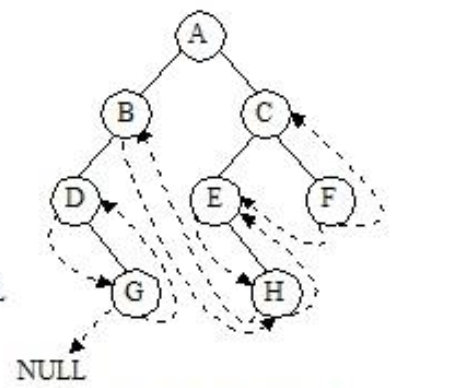
- 对于n个结点的二叉树,在二叉链存储结构中有n+1个空链域,利用这些空链域存放在某种遍历次序下该结点的前驱结点和后继结点的指针,这些指针称为线索,加上线索的二叉树称为线索二叉树。根据线索性质的不同,线索二叉树可分为前序线索二叉树、中序线索二叉树和后序线索二叉树三种。
typedef struct TNode {
char data; //节点数据
int ltag,rtag; //左右标志
struct TNode *lchild; //左孩子指针
struct TNode *rchild; //右孩子指针
}TNode,*Tree;
举例:
原二叉树
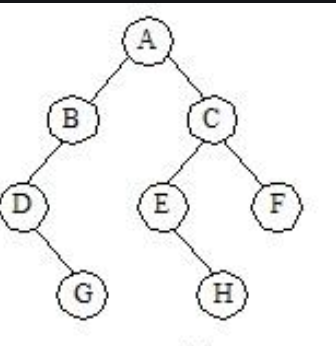
先序线索二叉树
中序线索二叉树
后序线索二叉树
哈夫曼树、并查集
- 哈夫曼树:具有最小带权路径长度的二叉树,也称最优树
结构体定义如下
typedef struct
{
int data;
double weight;
int parent;
int lchild;
int rchild;
}HTNode;
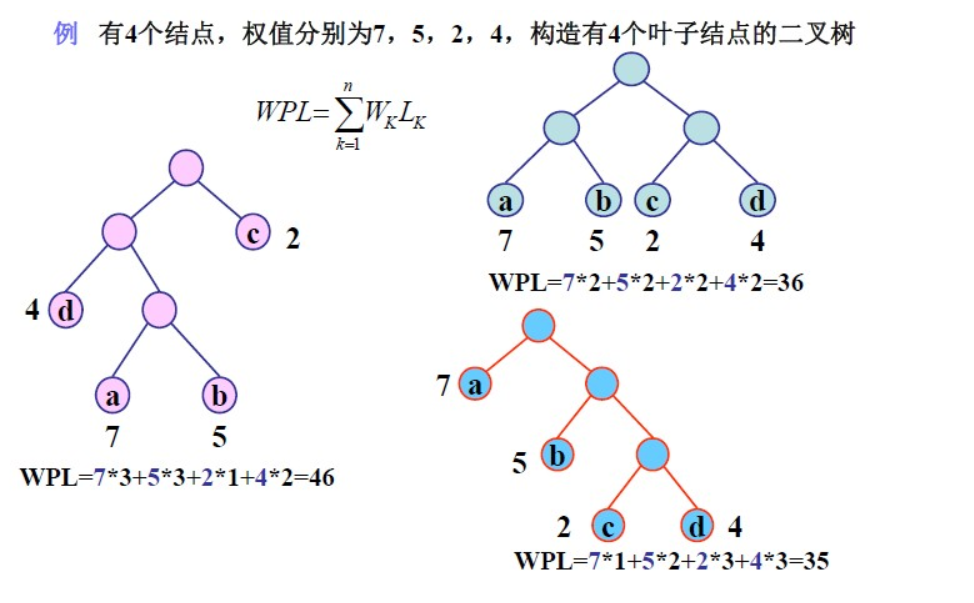
- 树的带权路径长度:如果树中每个叶子上都带有一个权值,则把树中所有叶子的带权路径长度之和称为树的带权路径长度。
设某二叉树有n个带权值的叶子结点,则该二叉树的带权路径长度记为
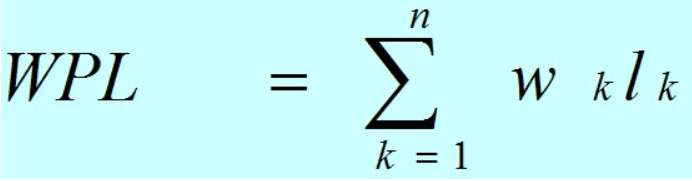
(公式中,Wk为第k个叶子结点的权值;Lk为该结点的路径长度。)
- 哈夫曼树的构建
void CreateHt(HTNode ht[], int n)
{
int i, j, k;
int lnode, rnode;
int min1, min2;
for (i = n; i < 2 * n - 1; i++)
{
min1=min2=1000;
lnode = rnode = -1;
ht[i].parent = -1; //初始化结点
for (k = 0; k < i ; k++) //在ht[0..i-1]中找权值最小的两个节点
{
if (ht[k].parent == -1) //只在尚未构造二叉树的节点中查找
{
if (ht[k].data < min1) //找最小值min1,使得左子树为min1
{
min2 = min1;
rnode = lnode;
min1 = ht[k].data;
lnode = k;
}
else if(ht[k].data < min2) //找次小值min2,使得右子树为min2
{
min2 = ht[k].data;
rnode = k;
}
}
}
ht[lnode].parent = i;
ht[rnode].parent = i;
ht[i].data = ht[lnode].data + ht[rnode].data;
ht[i].lchild = lnode;
ht[i].rchild = rnode; //ht[i]作为双亲节点
}
}
1.2.谈谈你对树的认识及学习体会。
2.阅读代码(0--5分)
2.1 题目及解题代码
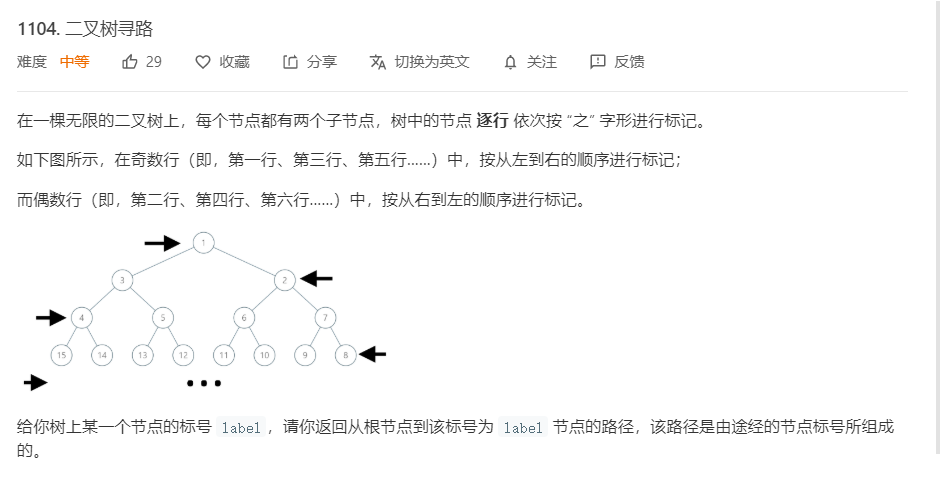

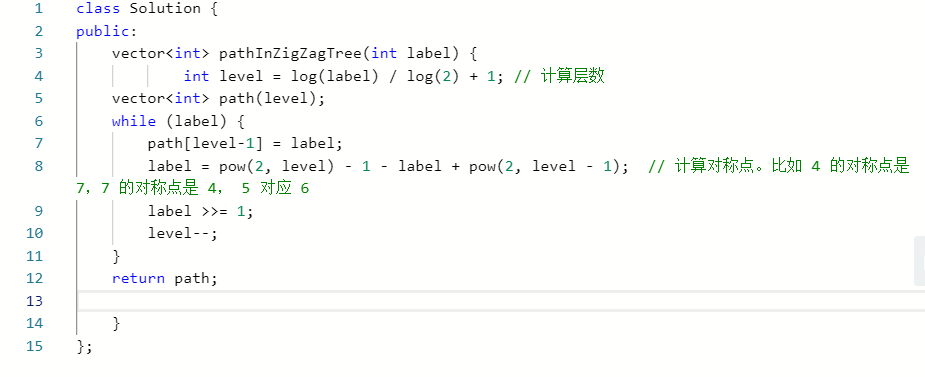
2.1.1 该题的设计思路
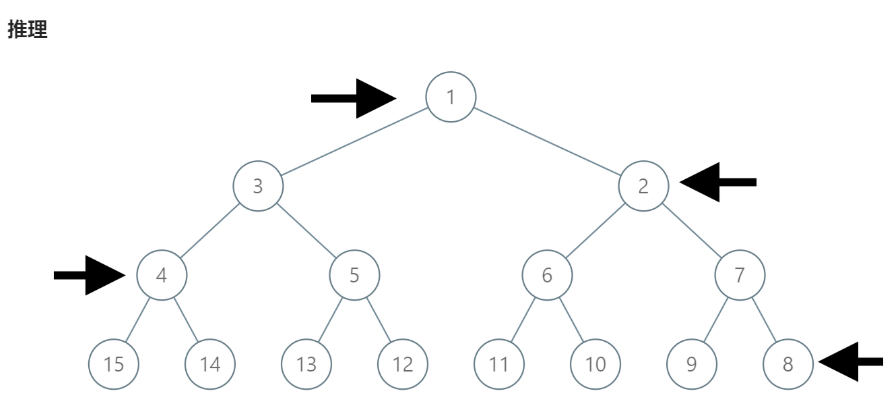
如果是按照正常顺序构造二叉树,理应是
1
2 3
4 5 6 7
8 9 10 11 12 13 14 15
....
2.1.2 该题的伪代码
class Solution {
public:{
计算层数
用level储存
while(label)
{
计算对称点。比如 4 的对称点是 7,7 的对称点是 4, 5 对应 6
}end while
}
2.1.3 运行结果

2.1.4分析该题目解题优势及难点。
- 本题难点即为找对称点
因为题目给出的是个完全二叉树,下一层的节点是当前层的2倍。
假设 label = 14label=14,顺序构造的上一层 label / 2 = 7label/2=7
但是按照原图来看理应是4才符合结果 。
假设 label = 11label=11,顺序构造的上一层 label / 2 = 5label/2=5
但是按照原图来看理应是6才符合结果。
此时可以看到按照之行排列的计算结果是顺序排列的 对称点
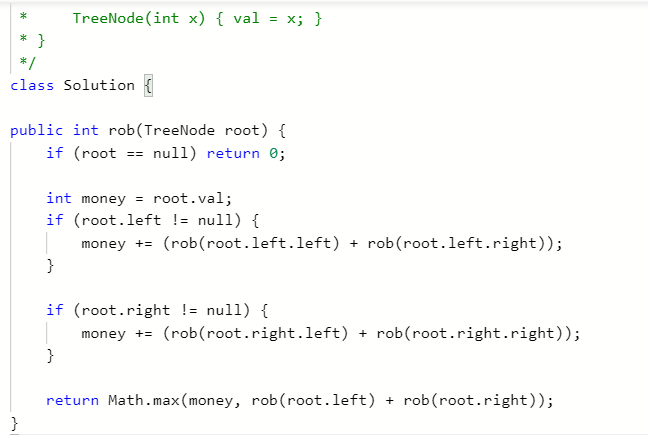
2.2 题目及解题代码

2.2.2 该题的伪代码
public int rob(TreeNode root) {
判断是否为空
对根的左右子树判断是否为空
若否爷爷与孙子进行递归操作
用money1,money2储存最后值
返回较大者
}
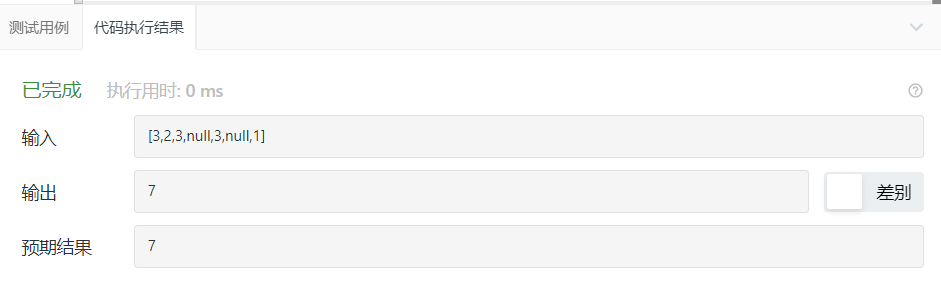
2.2.3 运行结果
2.2.4分析该题目解题优势及难点。
- 本题目本身就是动态规划的树形版本,可以了解一下树形问题在动态规划问题解法
本题可以将树看成孙子,儿子,和爷爷节点,题目要求求能偷盗的最多数是多少,即有几种情况,爷爷和孙子,儿子和儿子,具体要看给的树之间的关系,但是关键就是抓住不能直接相连来解体
2.3 题目及解题代码


2.3.2 该题的伪代码
class Solution {
public:
TreeNode* deleteNode(TreeNode* root, int key) {
如果key大于root->val, 递归到右子树删除
return root;
如果key小于root->val, 递归到左子树删除
return root;
如果key = root->val,且左子为null,根变成右子根
如果key = root->val, 且右子为null,根变成左子根
delete root;
return tmp;
找到右子树中最小值,与root->val交换
再在交换过的树中删除key
return root;
}
};
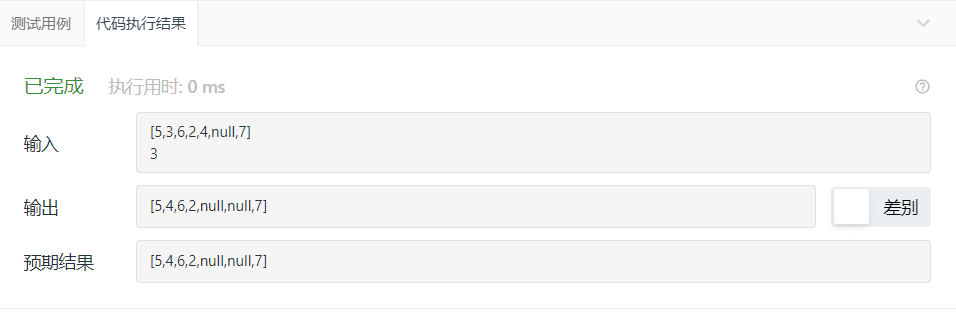
2.3.3 运行结果
2.3.4分析该题目解题优势及难点。
本题需要注意的是,在删除一个节点之后,有三种情况,一种是删除的是叶子节点,一种是删除根节点,左孩子补上,另一种是右孩子补上
2.4 题目及解题代码
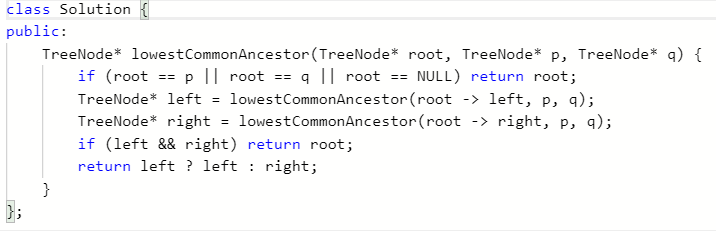
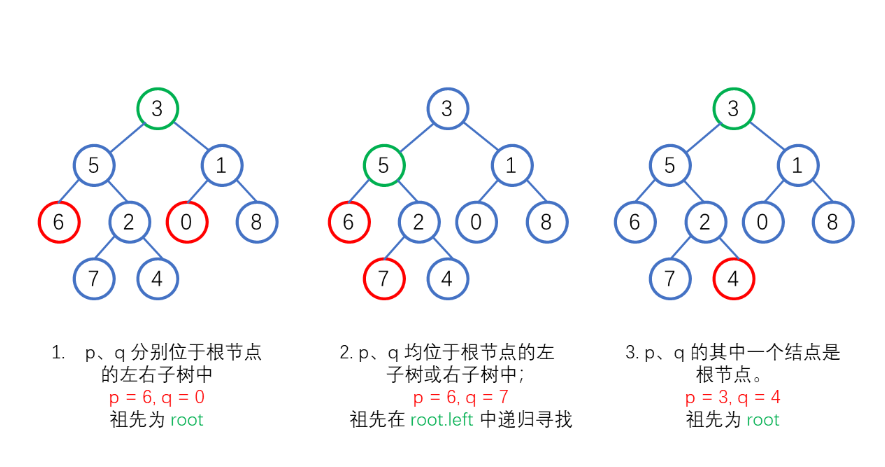
2.4.3 运行结果
2.4.4分析该题目解题优势及难点。
- 难点在于如何书写递归函数
假设我们从跟结点开始,向下遍历,如果当前结点到达叶子结点下的空结点时,返回空;如果当前结点为 p 或 q 时,返回当前结点
如果在左子树中找到了 p 或 q,left 会等于 p 或 q,同理,right 也是一样
然后我们进行判断:如果 left 为 right 都不为空,则为情况 1;如果 left 和 right 中只有一个不为空,说明这两个结点在子树中,则根节点到达子树再进行寻找