DS博客作业03-树

这个作业属于哪个班级	数据结构--网络2011/2012
这个作业的地址	DS博客作业03--树
这个作业的目标	学习树结构设计及运算操作
姓名	李雷默

0.PTA得分截图

1.本周学习总结

1.1 二叉树结构

1.1.1 二叉树的2种存储结构

• 顺序存储结构
  优点：存储空间利用率高。缺点：插入或删除元素时不方便。

• 链式存储
  优点：插入或删除元素时方便。缺点：存储空间利用率低。

1.1.2 二叉树的构造

构造二叉树，就是根据两个遍历序列推算出二叉树的结构。其中一个序列必须有一个是中序遍历序列，另一个可以是前序/后序/层次遍历序列。

1. 确定树的根节点：先序遍历的第一个节点
   求解树的子树：找出根节点在中序遍历中的位置，根左边的是左子树，右边的是右子树。

2. 确定树的根节点：后序遍历的最后一个节点
   求解树的子树：找出根节点在中序遍历中的位置，根左边的是左子树，右边的是右子树。

3. 确定树的根节点：层次遍历的第一个节点
   求解树的子树：找出根节点在中序遍历中的位置，根左边的是左子树，右边的是右子树。

1.1.3 二叉树的遍历

1. 先序遍历：访问根节点；访问当前节点的左子树；若当前节点无左子树，则访问当前节点的右子树。

2. 中序遍历：访问当前节点的左子树；访问根节点；访问当前节点的右子树。

3. 后序遍历：从根节点出发，依次遍历各节点的左右子树，直到当前节点左右子树遍历完成后，才访问该节点元素。

4. 层次遍历：通过使用队列的数据结构，从树的根结点开始，依次将其左孩子和右孩子入队。而后每次队列中一个结点出队，都将其左孩子和右孩子入队，直到树中所有结点都出队，出队结点的先后顺序就是层次遍历的最终结果。

1.1.4 线索二叉树

• 建立线索二叉树，或者说对二叉树线索化，实质上就是遍历一棵二叉树。在遍历过程中，访问结点的操作是检查当前的左，右指针域是否为空，将它们改为指向前驱结点或后续结点的线索。为实现这一过程，设指针pre始终指向刚刚访问的结点，即若指针p指向当前结点，则pre指向它的前驱，以便设线索。
  另外，在对一颗二叉树加线索时，必须首先申请一个头结点，建立头结点与二叉树的根结点的指向关系，对二叉树线索化后，还需建立最后一个结点与头结点之间的线索。

• 中序线索二叉树:若结点的ltag=1，lchild指向其前驱;否则，该结点的前驱是以该结点为根的左子树上按中序遍历的最后一个结点。若rtag=1，rchild指向其后继;否则，该结点的后继是以该结点为根的右子树上按中序遍历的第一个结点。

1.2 多叉树结构

1.2.1 多叉树结构

孩子兄弟链存储结构是为每个结点设计3个域，即一个数据元素域、一个指向该结点的左边第一个孩子结点的指针域、一个指向该结点的下一个兄弟结点的指针域。

1.2.2 多叉树遍历

与二叉树的先序遍历相同

1.3 哈夫曼树

1.3.1 哈夫曼树定义

当用 n 个结点（都做叶子结点且都有各自的权值）试图构建一棵树时，如果构建的这棵树的带权路径长度最小，称这棵树为“最优二叉树”，有时也叫“赫夫曼树”或者“哈夫曼树”。
在构建哈弗曼树时，要使树的带权路径长度最小，只需要遵循一个原则，那就是：权重越大的结点离树根越近。

1.3.2 哈夫曼树的结构体

对于给定的有各自权值的 n 个结点，构建哈夫曼树有一个行之有效的办法：

1. 在n个权值中选出两个最小的权值，对应的两个结点组成一个新的二叉树，且新二叉树的根结点的权值为左右孩子权值的和；
2. 在原有的n个权值中删除那两个最小的权值，同时将新的权值加入到n–2个权值的行列中，以此类推；
3. 重复1和2，直到所以的结点构建成了一棵二叉树为止，这棵树就是哈夫曼树。

1.3.2 哈夫曼树构建及哈夫曼编码

哈夫曼编码是一种变长编码。其定义如下：
对于给定的字符集D={d1,d2,...,dn}及其频率分布F={w1,w2,...,wn}，用d1,d2,...,dn作为叶结点，w1,w2,...,wn作为结点的权，利用哈夫曼算法构造一棵最优二叉树，将树中每个分支结点的左分支标上"0"；右分支标上"1"，把从根到每个叶子的路径符号("0"或"1")连接起来，作为该叶子的编码。
哈夫曼编码是在哈夫曼树的基础上求出来的，其基本思想是：从叶子结点di(0<=i<n)出发，向上回溯至根结点，依次求出每个字符的编码。

示例：对于字符集D={A，B，C，D}，其频率(单位：千次)分布为F={12，6，2，18}，下图给出D的哈夫曼编码图。

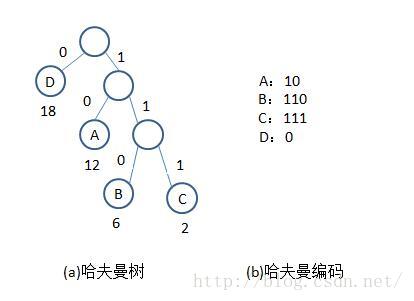
哈夫曼编码的回溯步骤如下：
       (1)选出哈夫曼树的某一个叶子结点。
       (2)利用其双亲指针parent找到其双亲结点。
       (3)利用找到的双亲结点的指针域中的lchild和rchild，判断该结点是双亲的左孩子还是右孩子。若该结点是其双亲结点的左孩子，则生成代码0；若该结点是其双亲结点的右孩子，则生成代码1。
       (4)由于生成的编码与要求的编码反序，将所生成的编码反序。
       (5)重复步骤(1)~(4)，直到所有结点都回溯完。

1.4 并查集

• 并查集：在一些有N个元素的集合应用问题中，我们通常是在开始时让每个元素构成一个单元素的集合，然后按一定顺序将属于同一组的元素所在的集合合并，其间要反复查找一个元素在哪个集合中。这种集合就是并查集。

• 并查集是一种简单的用途广泛的集合. 并查集是若干个不相交集合，能够实现较快的合并和判断元素所在集合的操作，应用很多，如其求无向图的连通分量个数、最小公共祖先、带限制的作业排序，还有最完美的应用：实现Kruskar算法求最小生成树。

• 并查集主要由一个整型数组pre[ ]和两个函数find( )、join( )构成。数组 pre[ ] 记录了每个点的前驱节点是谁，函数 find(x) 用于查找指定节点 x 属于哪个集合，函数 join(x,y) 用于合并两个节点 x 和 y 。

查找：

int get_Parent(int x)
{
    if(node[x].parent==x)
        return x;
    return get_Parent(node[x].parent);
}

合并：

void Union(int x,int y)
{
    x=get_Parent(x);
    y=get_Parent(y);
    if(node[x].rank>node[y].rank)
       node[y].parent=x;
    else
       node[x].parent=y;
       if(node[x].rank==t[y].rank)
           node[y].rank++;
}

1.5.谈谈你对树的认识及学习体会。

大致上了解了树的类型、遍历、和应用，但不懂的地方还是很多，一如既往地对代码犯难，希望能花更多时间在代码上。

2.PTA实验作业

2.1 二叉树：输出二叉树每层节点

2.1.1 解题思路及伪代码

1.先序遍历递归创建二叉树
2.利用栈结构层序遍历输出结点

void LevelOrder(BTree bt)
{
    
    BinTree bt;
    if (空树) 
        退出
    根结点入队
    将树的每个节点输入队列
}
void LevelOrder(BinTree bt)
{
    int flag=1;
    while (栈不为空)
        {
	  记录层数
          如果层数改变，flag改变
	  如果换行，打印
	  先序遍历
	  入栈
	  出栈
	  flag置零;
	}
}

2.1.2 总结解题所用的知识点

先序遍历建立二叉树，还可以用队列或栈层次遍历二叉树。

2.2 目录树

2.2.1 解题思路及伪代码

判断是目录还是文件，目录优先文件存放，没有目录则新建

2.2.2 总结解题所用的知识点

用兄弟孩子链表来构建目录树

3.阅读代码

3.1 题目及解题代码

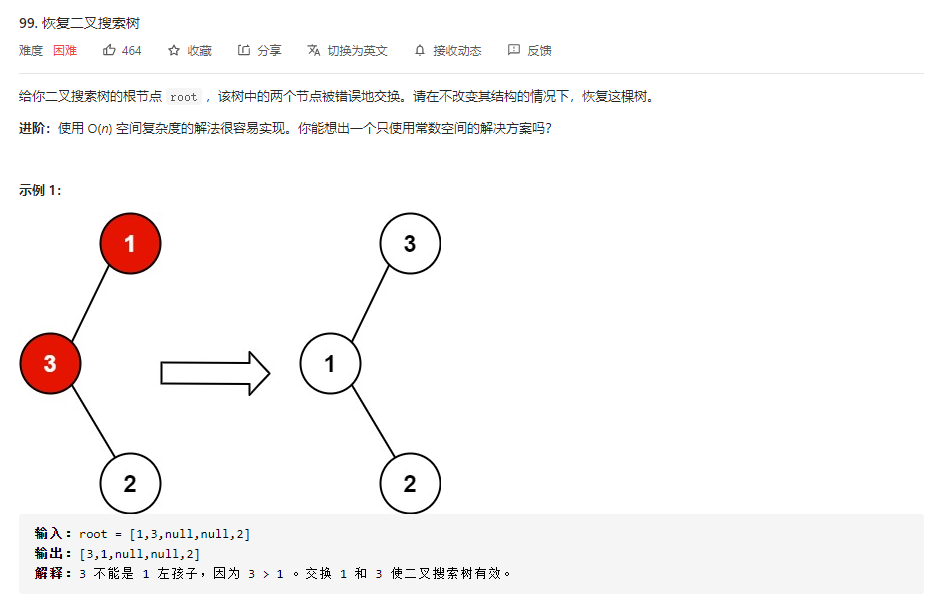
class Solution {
    public void recoverTree(TreeNode root) {
        List<Integer> nums = new ArrayList<Integer>();
        inorder(root, nums);
        int[] swapped = findTwoSwapped(nums);
        recover(root, 2, swapped[0], swapped[1]);
    }

    public void inorder(TreeNode root, List<Integer> nums) {
        if (root == null) {
            return;
        }
        inorder(root.left, nums);
        nums.add(root.val);
        inorder(root.right, nums);
    }

    public int[] findTwoSwapped(List<Integer> nums) {
        int n = nums.size();
        int x = -1, y = -1;
        for (int i = 0; i < n - 1; ++i) {
            if (nums.get(i + 1) < nums.get(i)) {
                y = nums.get(i + 1);
                if (x == -1) {
                    x = nums.get(i);
                } else {
                    break;
                }
            }
        }
        return new int[]{x, y};
    }

    public void recover(TreeNode root, int count, int x, int y) {
        if (root != null) {
            if (root.val == x || root.val == y) {
                root.val = root.val == x ? y : x;
                if (--count == 0) {
                    return;
                }
            }
            recover(root.right, count, x, y);
            recover(root.left, count, x, y);
        }
    }
}

3.2 该题的设计思路及伪代码

时间复杂度：O(N)O(N)，其中 NN 为二叉搜索树的节点数。中序遍历需要 O(N)O(N) 的时间，判断两个交换节点在最好的情况下是 O(1)O(1)，在最坏的情况下是 O(N)O(N)，因此总时间复杂度为 O(N)O(N)。
空间复杂度：O(N)O(N)。我们需要用 extit{nums}nums 数组存储树的中序遍历列表。

设计思路：具体来说，由于我们只关心中序遍历的值序列中每个相邻的位置的大小关系是否满足条件，且错误交换后最多两个位置不满足条件，因此在中序遍历的过程我们只需要维护当前中序遍历到的最后一个节点 extit{pred}pred，然后在遍历到下一个节点的时候，看两个节点的值是否满足前者小于后者即可，如果不满足说明找到了一个交换的节点，且在找到两次以后就可以终止遍历。
这样我们就可以在中序遍历中直接找到被错误交换的两个节点 xx 和 yy，不用显式建立 extit{nums}nums 数组。

3.3 分析该题目解题优势及难点。

采用中序遍历，容易理解，但采取了迭代实现的写法，不易读懂代码。