[数论][组合数学]fireworks

Problem Description

Hmz likes to play fireworks, especially when they are put regularly.
Now he puts some fireworks in a line. This time he put a trigger on each firework. With that trigger, each firework will explode and split into two parts per second, which means if a firework is currently in position x, then in next second one part will be in position x−1 and one in x+1. They can continue spliting without limits, as Hmz likes.
Now there are n fireworks on the number axis. Hmz wants to know after T seconds, how many fireworks are there in position w?

Input

Input contains multiple test cases.
For each test case:

• The first line contains 3 integers n,T,w(n,T,|w|≤10^5)
• In next n lines, each line contains two integers xi and ci, indicating there are ci fireworks in position xi at the beginning(ci,|xi|≤10^5).

Output

For each test case, you should output the answer MOD 1000000007.

Sample Input

1 2 0
2 2
2 2 2
0 3
1 2

Sample Output

2
3

思路：

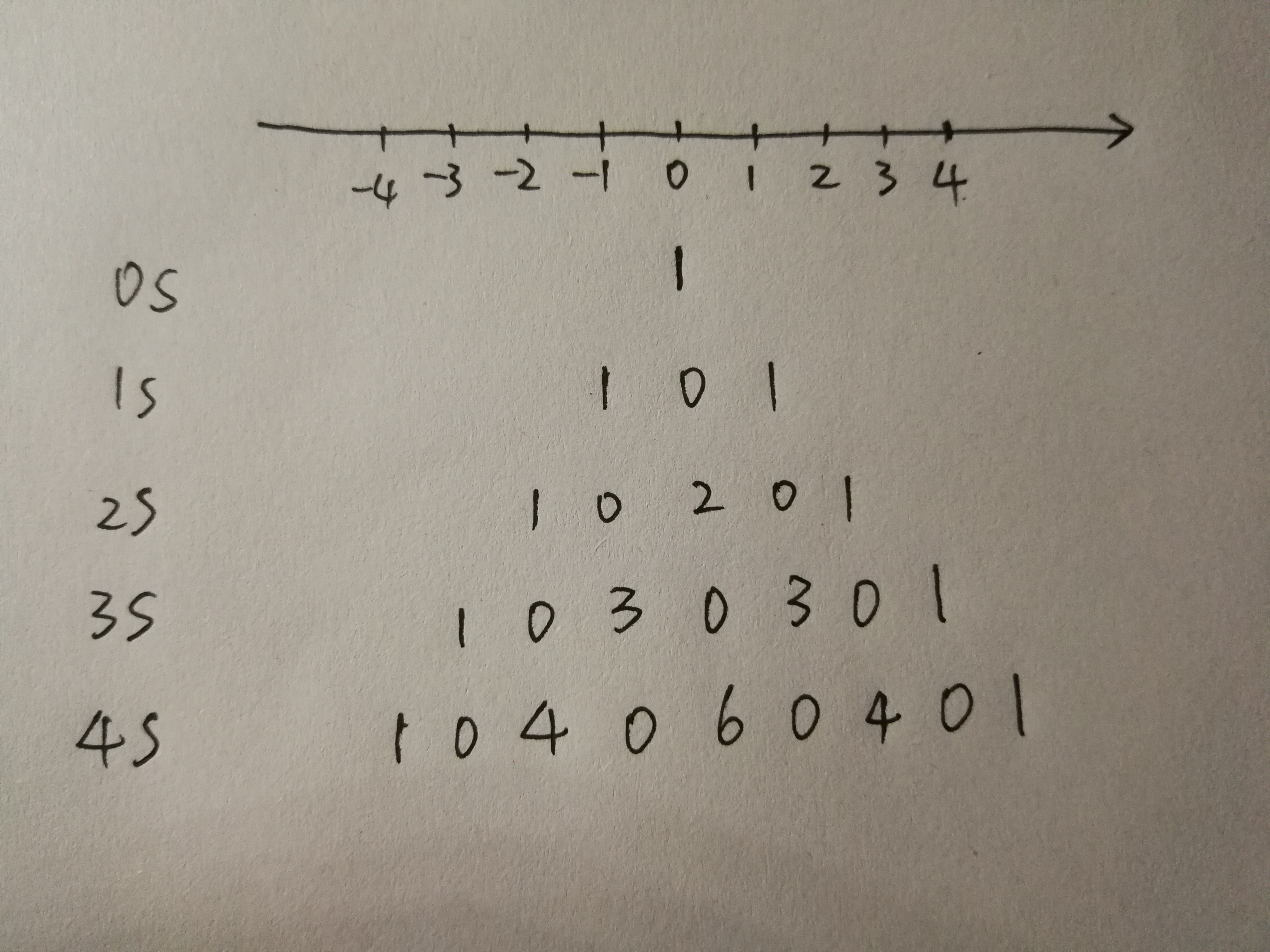若0s时烟花在x=0处，则t=2,3,4...s时，各个位置处的烟花数量如图所示，发现它们构成一个杨辉三角。于是可以知道，t s时，在位置(0-t)+k*2（0<=k<=t）处的烟花数量为C(t,k)，其他位置的烟花数量为0。所以给定烟花的初始位置x和经过的时间t，可以算出在位置w的烟花数量

AC代码：

#include <iostream>
#include<cstdio>
#define ll long long
#define mod 1000000007
using namespace std;

ll f[100010];

void init(){//预处理n!
  f[0]=1;
  for(ll i=1;i<=100005;i++){
    f[i]=i*f[i-1]%mod;
  }
}

ll qpow(ll x,ll n){
  ll ret=1;
  while(n){
     if(n&1) ret=(ret*x)%mod;
     x=(x*x)%mod;
     n>>=1;
  }
  return ret;
}

ll rev(ll x){
  return qpow(x,mod-2);
}

ll C(ll n,ll m){//利用逆元求组合数
  return f[n]%mod*rev(f[m])%mod*rev(f[n-m])%mod;
}

int main()
{
    init();
    ll n,t,w;
    while(scanf("%lld%lld%lld",&n,&t,&w)!=EOF){
        ll ans=0;
        for(ll i=1;i<=n;i++){
            ll x,c;
            scanf("%lld%lld",&x,&c);
            ll stax=x-t;
            if((w-stax)%2!=0) continue;
            else{
                ll k=(w-stax)/2;
                if(k<0||k>t) continue;
                else ans=(ans+(c*C(t,k))%mod)%mod;
            }
        }
        printf("%lld
",ans);
    }
    return 0;
}