题目描述
1.如果现在在第i个格子,则可以跳到第Ai个格子。
2.把某个Ai增加或减少1。
nm开始在第1个格子,他需要走到第N个格子才能通关。现在他已经头昏脑涨啦,需要你帮助他求出,从起点到终点最少需要多少次操作。
输入
输出
样例输入
5
3 4 2 5 3
样例输出
3
提示
•对于30%的数据,1≤N≤10。
•对于60%的数据,1≤N≤1,000。
•对于100%的数据,1≤N≤100,000,1≤Ai≤N。
题目大意:很清楚了,就不解释了。
思路:建立图模型(如下),会发现其实等价于求起点到终点的最短路(bfs或几种最短路算法)。
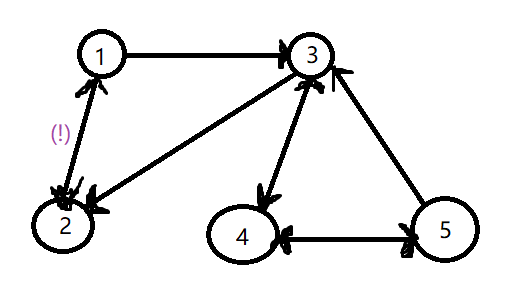 (样例:3 4 2 5 3,起点1,终点5,答案3)
(样例:3 4 2 5 3,起点1,终点5,答案3)
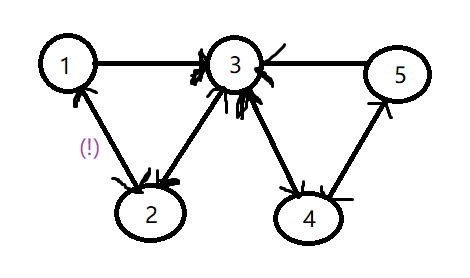 (样例:3 3 3 3 3 ,起点1,终点5,答案3)
(样例:3 3 3 3 3 ,起点1,终点5,答案3)
如何建立此图模型:
1.建立起i到Ai的单向边,权值为1,表明从i到Ai需要操作1步;
2.建立起i与i-1(如果存在的话),i与i+1(如果存在的话)的双向边,权值也都为1;
(比如说有a[2]=4,那么不光要建立2到4的单向边,也要建立4与3,4与5的双向边)
这个要好好理解,根据题意,可以对任意Ai加或减1,并算做一步操作,于是可以理解为:虽然a[2]=4(也就是2可以跳到4),但对a[2]进行加减1操作后,就意味着2也可以到3或5,当然操作数数也要加上1,所以建立相邻数的双向边意思是相邻数其实可以互通(对应着加减1操作),比如有a[2]=4,a[4]=1的话,当2跳到4后,4可以跳到1,3或5,同理接着5(假如上一步跳到了5)可以跳到a[5],4或者6...,那么从2到6的过程可以看作是2->4->5->6(等价于把a[2]加1再加1变成6后跳到6)。
可以自己再琢磨一下上面两个图。
还有需要明白的是,对于所在位置i的下一位置a[i],i-1,i+1在bfs中属于同一层。
注意(!):
在bfs中起点不能是1,因为这样的话a[1]和2将被1更新并被加入队列,“更新”也就是1->a[1]使到达a[1]的最少步数f[a[1]]变为f[1]+1=0+1=1,同理1->2使得f[2]变为f[1]+1=1,答案显然是不对的(因为按此法要2步操作),所以起点1处有点特殊,不能用它来更新2(即不能从head=1(f[head]=0)开始进行bfs),所以我们从head=a[1](f[head]=1)开始进行bfs。
AC代码:
#include<cstdio> #include<cstring> #include<queue> #define inf 0x3f3f3f3f using namespace std; int n; int a[100010]; int f[100010]; int vis[100010]; void bfs(){ queue<int > q; while(!q.empty()) q.pop(); f[1]=0; vis[1]=1; int head=a[1]; f[head]=1; vis[head]=1; q.push(head); while(!q.empty()){ head=q.front(); q.pop(); if(!vis[a[head]]){ vis[a[head]]=1; if(f[a[head]]>f[head]+1) f[a[head]]=f[head]+1; q.push(a[head]); } if(head-1>=1&&!vis[head-1]){ vis[head-1]=1; if(f[head-1]>f[head]+1) f[head-1]=f[head]+1; q.push(head-1); } if(head+1<=n&&!vis[head+1]){ vis[head+1]=1; if(f[head+1]>f[head]+1) f[head+1]=f[head]+1; q.push(head+1); } } } int main() { scanf("%d",&n); for(int i=1;i<=n;i++){ scanf("%d",&a[i]); } memset(vis,0,sizeof(vis)); memset(f,0x3f,sizeof(f)); bfs(); printf("%d ",f[n]); return 0; }
总结:对于图论题,关键是等价建立图模型。