题目描述
There are n rectangle radar scanners on the ground. The sides of them are all paralleled to the axes. The i-th scanner's bottom left corner is square (ai,bi) and its top right corner is square (ci,di). Each scanner covers some squares on the ground.
You can move these scanners for many times. In each step, you can choose a scanner and move it one square to the left, right, upward or downward.
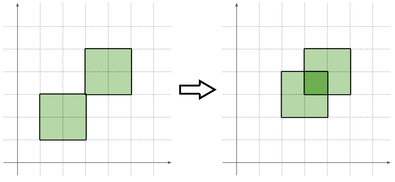
Today, the radar system is facing a critical low-power problem. You need to move these scanners such that there exists a square covered by all scanners.
Your task is to minimize the number of move operations to achieve the goal.
You can move these scanners for many times. In each step, you can choose a scanner and move it one square to the left, right, upward or downward.

Today, the radar system is facing a critical low-power problem. You need to move these scanners such that there exists a square covered by all scanners.
Your task is to minimize the number of move operations to achieve the goal.
输入
The first line of the input contains an integer T(1≤T≤1000), denoting the number of test cases.
In each test case, there is one integer n(1≤n≤100000) in the first line, denoting the number of radar scanners.
For the next n lines, each line contains four integers ai,bi,ci,di(1≤ai,bi,ci,di≤109,ai≤ci,bi≤di), denoting each radar scanner.
It is guaranteed that ∑n≤106.
In each test case, there is one integer n(1≤n≤100000) in the first line, denoting the number of radar scanners.
For the next n lines, each line contains four integers ai,bi,ci,di(1≤ai,bi,ci,di≤109,ai≤ci,bi≤di), denoting each radar scanner.
It is guaranteed that ∑n≤106.
输出
For each test case, print a single line containing an integer, denoting the minimum number of steps.
样例输入 Copy
1
2
2 2 3 3
4 4 5 5
样例输出 Copy
2
题意:给定n个矩形,可以上下左右移动,求要使有一个格子被所有矩形覆盖,最小要移动的次数。
思路:两维独立,单独考虑每一维。对于矩形(x1,y1) (x2,y2),投影到x轴上可等价于线段[x1,x2],问题转化为求所有线段移动到同一公共点的最小移动距离。即最小化∑[(x1[i]-x)+(x2[i]-x)-(x2[i]-x1[i])]/2。可以看出,x取x1[]和x2[]的中位数时,该值最小。另一维同理。