题意:输入a,b,p,求 (底数a的右上角有b-1个a)
(底数a的右上角有b-1个a)
思路:
广义欧拉定理:
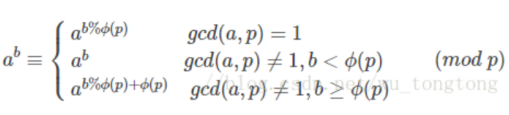
AC代码:

#include<bits/stdc++.h> typedef long long ll; using namespace std; ll a,b,m; ll vis[1000005]; ll prime[1000005],num=0; ll phi[1000005]; void getphi(ll n=1000000){ phi[1]=1; for(ll i=2;i<=n;i++){ if(!vis[i]) prime[++num]=i,phi[i]=i-1; for(ll j=1;j<=num;j++){ ll k=i*prime[j]; if(k>n)break; vis[k]=1; if(i%prime[j]==0){ phi[k]=phi[i]*prime[j]; break; } phi[k]=phi[i]*(prime[j]-1); } } return; } ll qpow(ll a,ll b,ll mod){ ll ret=1; while(b){ if(b&1) ret=ret*a%mod; a=a*a%mod; b>>=1; } return ret; } ll check(ll d,ll cmp){ ll res=a; for(ll i=1;i<=d;i++){ ll tmp=1; for(ll j=1;j<=res;j++){ tmp=tmp*a; if(tmp>=cmp) return 1; } res=tmp; } return -1; } ll fun(ll d){ ll res=a; for(ll i=1;i<=d;i++){ ll tmp=1; for(ll j=1;j<=res;j++) tmp=tmp*a; res=tmp; } return res; } ll cal(ll d,ll p){ if(p==1) return 0; if(d==0) return a%p; ll tmp; if(__gcd(a,p)==1) tmp=cal(d-1,phi[p]);//gcd(a,p)==1 else{ if(check(d-1,phi[p])<0) tmp=fun(d-1);//gcd(a,p)!=1&&b<phi(p) else tmp=cal(d-1,phi[p])+phi[p];//gcd(a,p)!=1&&b>=phi(p) } ll ret=qpow(a,tmp,p); return ret; } int main() { getphi(); ll t;scanf("%lld",&t); while(t--){ scanf("%lld%lld%lld",&a,&b,&m); if(a==1||b==0){ printf("%lld ",1%m); continue; } ll ans=cal(b-1,m); printf("%lld ",ans%m); } return 0; }
