Description
In how many ways can you tile a 3xn rectangle with 2x1 dominoes?
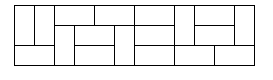
Here is a sample tiling of a 3x12 rectangle.
Input
Input consists of several test cases followed by a line containing -1. Each test case is a line containing an integer 0 <= n <= 30.
Output
For each test case, output one integer number giving the number of possible tilings.
Sample Input
2 8 12 -1
Sample Output
3 153 2131
题解
看了别人的博客都是递推啥的,
之前自己推了半天推不出来,智商捉鸡,就放着没做了
直到我做了POJ 2411后
再回来看这题,就是把宽度设为3而已...
#include <iostream> #include <cstdio> //EOF,NULL #include <cstring> //memset #include <cmath> //ceil,floor,exp,log(e),log10(10),hypot(sqrt(x^2+y^2)),cbrt(sqrt(x^2+y^2+z^2)) #include <algorithm> //fill,reverse,next_permutation,__gcd, #include <string> #include <vector> #include <queue> #include <stack> #include <map> using namespace std; #define rep(i, a, n) for (int i = a; i < n; ++i) #define sca(x) scanf("%d", &x) #define sca2(x, y) scanf("%d%d", &x, &y) #define sca3(x, y, z) scanf("%d%d%d", &x, &y, &z) #define pri(x) printf("%d ", x) #define pb push_back #define mp make_pair typedef pair<int, int> P; typedef long long ll; const ll inf = 99999999999; const int INF = 0x3f3f3f3f; const int mod = 1e9+7; const int maxn = 105; const int N = 1e4 + 5; int t, n, m; int cnt, ans, ed; ll dp[31][1<<4]; int path[50000][2]; int h, w; void dfs(int l, int now, int pre) { if (l > w) { return; } if (l == w) { path[cnt][0] = pre; path[cnt++][1] = now; return; } dfs(l + 2, (now << 2)|3, (pre << 2)|3); // 竖放,当前行为1,上一行为0 dfs(l + 1, (now << 1)|1, (pre << 1)); // 横放 当前行和上一行都为11 dfs(l + 1, (now << 1), (pre << 1)|1); //不放,上一行为1,当前行为0 } int main() { while (sca(h) && h != -1) { w = 3; cnt = 0; dfs(0, 0, 0); memset(dp, 0, sizeof dp); ed = (1 << w) - 1; dp[0][ed] = 1; for (int i = 0; i < h; i++) { for (int j = 0; j < cnt; j++) { dp[i + 1][path[j][1]] += dp[i][path[j][0]]; } } printf("%lld ", dp[h][ed]); } return (0); }