本文算法使用python3实现
1.题目描述:
用两个栈来实现一个队列,完成队列的Push和Pop操作。 队列中的元素为int类型。
时间限制:1s;空间限制:32768K
2.思路描述:
将栈stack1作为存储空间,栈stack2作为临时缓冲区。
入队操作:将元素压入stack1中
出队操作:
(1)判断stack1与stack2是否同时为空,若是,则抛出异常。否则,进行(2)
(2)判断stack2是否为空,若为空,将stack1中的2~n个元素“倒入”stack2中,弹出stack1中的元素。否则,进行(3)
(3)直接弹出stack2中的栈顶元素。
参考示意图:
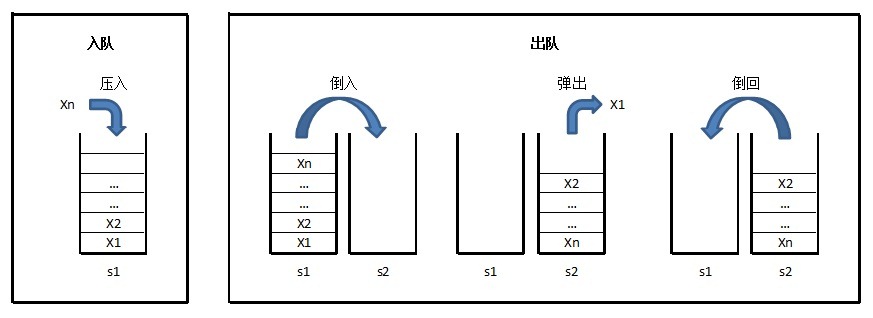
3.对于以下问题进行以下解释:
(1)在入队时为何不对stack1进行判断是否为空?
答:当stack1不为空时,此时stack1中的元素,从栈底到栈顶元素是按时间先后顺序压入的,此时将元素压入stack1中,如果再进行出队操作时会先判断stack2中是否有元素(参考上面出队操作),而stack2中的元素入队列的时间始终比stack1中的早;就算stack2中没有元素,也会将stack1中的元素先“倒入”stack2中,再出队,此时出队的元素为原始stack1中栈底元素,即最早进入队列的元素。因此,判断与否都不会影响结果。
(2)为何将stack1中的2~n个元素“倒入”stack2中,而不是全部“倒入”?
答:这样可以减少一次压栈操作
4.程序代码:
class Solution:
def __init__(self):
self.stack1 = []
self.stack2 = []
def push(self, node):
'''入队操作'''
self.stack1.append(node)
def pop(self):
'''出队操作'''
# 操作(1)
if len(self.stack1) == 0 and len(self.stack2) == 0:
print('队列为空!')
return
# 操作(3)
if len(self.stack2) != 0:
return self.stack2.pop()
else:
# 操作(2)
while len(self.stack1) > 1:
self.stack2.append(self.stack1[-1])
del self.stack1[-1]
return self.stack1.pop()