比赛链接:http://codeforces.com/contest/569
Little Lesha loves listening to music via his smartphone. But the smartphone doesn't have much memory, so Lesha listens to his favorite songs in a well-known social network InTalk.
Unfortunately, internet is not that fast in the city of Ekaterinozavodsk and the song takes a lot of time to download. But Lesha is quite impatient. The song's duration isT seconds. Lesha downloads the first S seconds of the song and plays it. When the playback reaches the point that has not yet been downloaded, Lesha immediately plays the song from the start (the loaded part of the song stays in his phone, and the download is continued from the same place), and it happens until the song is downloaded completely and Lesha listens to it to the end. Forq seconds of real time the Internet allows you to downloadq - 1 seconds of the track.
Tell Lesha, for how many times he will start the song, including the very first start.
The single line contains three integers T, S, q (2 ≤ q ≤ 104,1 ≤ S < T ≤ 105).
Print a single integer — the number of times the song will be restarted.
5 2 2
2
5 4 7
1
6 2 3
1
In the first test, the song is played twice faster than it is downloaded, which means that during four first seconds Lesha reaches the moment that has not been downloaded, and starts the song again. After another two seconds, the song is downloaded completely, and thus, Lesha starts the song twice.
In the second test, the song is almost downloaded, and Lesha will start it only once.
In the third sample test the download finishes and Lesha finishes listening at the same moment. Note that song isn't restarted in this case.
题目大意:一个人下载歌,每q个时间单位能下载q-1个时间单位的歌,歌的长度为T。下到S的时候開始播放,假设歌还没下完且放到了还未下载的地方。则重头開始放,问一共要放多少次
题目分析:一開始从s開始。设下了cur秒后听和下的进度同样,则 s + (q - 1) / q * cur = cur,解得cur = q * s,然后从头開始。设t'秒后进度同样,则(q - 1) / q * t' + cur = t'。解得t' = cur * q,可见直接拿第一次进度同样的时间乘q就是接下来每次进度同样的时间
#include <cstdio>
int main()
{
int T, S, q, ans = 1, cur;
scanf("%d %d %d", &T, &S, &q);
cur = q * S;
while(cur < T)
{
cur = q * cur;
ans ++;
}
printf("%d
", ans);
}
Companies always have a lot of equipment, furniture and other things. All of them should be tracked. To do this, there is an inventory number assigned with each item. It is much easier to create a database by using those numbers and keep the track of everything.
During an audit, you were surprised to find out that the items are not numbered sequentially, and some items even share the same inventory number! There is an urgent need to fix it. You have chosen to make the numbers of the items sequential, starting with 1. Changing a number is quite a time-consuming process, and you would like to make maximum use of the current numbering.
You have been given information on current inventory numbers forn items in the company. Renumber items so that their inventory numbers form apermutation of numbers from 1 to n by changing the number of as few items as possible. Let us remind you that a set ofn numbers forms a permutation if all the numbers are in the range from 1 to n, and no two numbers are equal.
The first line contains a single integer n — the number of items (1 ≤ n ≤ 105).
The second line contains n numbersa1, a2, ..., an (1 ≤ ai ≤ 105) — the initial inventory numbers of the items.
Print n numbers — the final inventory numbers of the items in the order they occur in the input. If there are multiple possible answers, you may print any of them.
3
1 3 2
1 3 2
4
2 2 3 3
2 1 3 4
1
2
1
In the first test the numeration is already a permutation, so there is no need to change anything.
In the second test there are two pairs of equal numbers, in each pair you need to replace one number.
In the third test you need to replace 2 by 1, as the numbering should start from one.
题目大意:给n个数,能够改变随意个数字的大小目标是将其改成1-n的一个排列,要求改变次数最小,输出排列
题目分析:记录原始序列已经在1-n位置的数,凡是大于n的或者反复出现的数字下标 标记一下。枚举一下1-n中还有哪些数字没出现。然后按顺序改动
#include <cstdio>
#include <cstring>
int const MAX = 1e5 + 5;
int a[MAX], need[MAX];
bool has[MAX], pos[MAX];
int main()
{
int n, num = 0;
scanf("%d", &n);
memset(has, false, sizeof(has));
memset(pos, false, sizeof(pos));
for(int i = 0; i < n; i++)
{
scanf("%d", &a[i]);
if(!has[a[i]] && a[i] <= n)
has[a[i]] = true;
else
pos[i] = true;
}
int cnt = 0;
for(int i = 1; i <= n; i++)
if(!has[i])
need[cnt ++] = i;
int idx = 0;
for(int i = 0; i < n; i++)
if(pos[i])
a[i] = need[idx ++];
for(int i = 0; i < n - 1; i++)
printf("%d ", a[i]);
printf("%d
", a[n - 1]);
}Rikhail Mubinchik believes that the current definition of prime numbers is obsolete as they are too complex and unpredictable. A palindromic number is another matter. It is aesthetically pleasing, and it has a number of remarkable properties. Help Rikhail to convince the scientific community in this!
Let us remind you that a number is called prime if it is integer larger than one, and is not divisible by any positive integer other than itself and one.
Rikhail calls a number a palindromic if it is integer, positive, and its decimal representation without leading zeros is a palindrome, i.e. reads the same from left to right and right to left.
One problem with prime numbers is that there are too many of them. Let's introduce the following notation:π(n) — the number of primes no larger thann, rub(n) — the number of palindromic numbers no larger thann. Rikhail wants to prove that there are a lot more primes than palindromic ones.
He asked you to solve the following problem: for a given value of the coefficientA find the maximum n, such that π(n) ≤ A·rub(n).
The input consists of two positive integers
p, q, the numerator and denominator of the fraction that is the value ofA (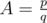 ,
, 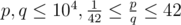 ).
).
If such maximum number exists, then print it. Otherwise, print"Palindromic tree is better than splay tree" (without the quotes).
1 1
40
1 42
1
6 4
172
题目大意:π(n) 为不大于n的素数个数,rub(n)为不大于n的回文数个数,A=p/q,如今要求最大的n,使得π(n) ≤ A·rub(n)
题目分析:预处理这两类数的个数,数组尽量往大了开吧,1e7过了
#include <cstdio>
#include <cstring>
#include <algorithm>
#define ll long long
using namespace std;
int const MAX = 1e7 + 5;
int cntpr[MAX], cntpa[MAX], p[MAX];
bool prime[MAX];
void get_prime()
{
int pnum = 1;
memset(cntpr, 0, sizeof(cntpr));
memset(prime, true, sizeof(prime));
for(int i = 2; i <= MAX; i++)
{
cntpr[i] = cntpr[i - 1];
if(prime[i])
{
cntpr[i] ++;
p[pnum ++] = i;
}
for(int j = 1; j <= pnum && i * p[j] < MAX; j++)
{
prime[i * p[j]] = false;
if(i % p[j] == 0)
break;
}
}
}
bool judge(int x)
{
char s[10];
sprintf(s, "%d", x);
int len = strlen(s);
for(int i = 0; i < len / 2; i++)
if(s[i] != s[len - i - 1])
return false;
return true;
}
void get_palindromes()
{
memset(cntpa, 0, sizeof(cntpa));
for(int i = 1; i <= MAX; i++)
{
cntpa[i] = cntpa[i - 1];
if(judge(i))
cntpa[i] ++;
}
}
int main()
{
bool flag = false;
int p, q;
int ans = 0;
get_prime();
get_palindromes();
scanf("%d %d", &p, &q);
for(int i = 1; i <= MAX; i++)
{
if((ll) q * cntpr[i] <= (ll) p * cntpa[i])
{
ans = max(ans, i);
flag = true;
}
}
if(flag)
printf("%d
", ans);
else
printf("Palindromic tree is better than splay tree
");
}Little Johnny has recently learned about set theory. Now he is studying binary relations. You've probably heard the term "equivalence relation". These relations are very important in many areas of mathematics. For example, the equality of the two numbers is an equivalence relation.
A set ρ of pairs (a, b) of elements of some setA is called a binary relation on set
A. For two elements
a and b of the set
A we say that they are in relationρ, if pair
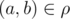 , in this case we use a notation
, in this case we use a notation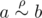 .
.
Binary relation is equivalence relation, if:
- It is reflexive (for any a it is true that
 );
); - It is symmetric (for any a,
b it is true that if
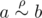 , then
, then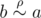 );
); - It is transitive (if
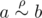 and
and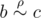 ,
than
,
than ).
).
Little Johnny is not completely a fool and he noticed that the first condition is not necessary! Here is his "proof":
Take any two elements, a and
b. If 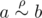 , then
, then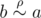 (according to property (2)), which means
(according to property (2)), which means (according to property (3)).
(according to property (3)).
It's very simple, isn't it? However, you noticed that Johnny's "proof" is wrong, and decided to show him a lot of examples that prove him wrong.
Here's your task: count the number of binary relations over a set of size n such that they are symmetric, transitive, but not an equivalence relations (i.e. they are not reflexive).
Since their number may be very large (not 0, according to Little Johnny), print the remainder of integer division of this number by109 + 7.
A single line contains a single integer n(1 ≤ n ≤ 4000).
In a single line print the answer to the problem modulo 109 + 7.
1
1
2
3
3
10
If n = 1 there is only one such relation — an empty one, i.e.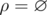 . In other words,
for a single elementx of set
A the following is hold:
. In other words,
for a single elementx of set
A the following is hold: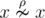 .
.
If n = 2 there are three such relations. Let's assume that setA consists of two elements,
x and y. Then the valid relations are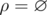 ,ρ = {(x, x)},
ρ = {(y, y)}. It is easy to see that the three listed binary relations are symmetric and transitive relations, but they are not equivalence relations.
,ρ = {(x, x)},
ρ = {(y, y)}. It is easy to see that the three listed binary relations are symmetric and transitive relations, but they are not equivalence relations.
题目大意:学过离散数学的同学理解起题意更快,求1到n,n个元素组成的集合中,满足对称性和传递性但不满足自反性的二元组关系集合的个数
题目分析:先结束下例子3,能够是
空集
{<a, a>}, {<b, b>},{<c, c>}
{<a, a>, <b, b>},{<a, a>, <c, c>},{<b, b>, <c, c>}
{<a, a>, <b, b>, <a, b>, <b, a>},{<b, b>, <c, c>, <b, c>, <c, b>},{<a, a>, <c, c>, <a, c>, <c, a>} 一共10个
由于每组等价关系的个数正好等于Bell数,所以不难推出ans[i] = Bell[i + 1] - Bell[i]。从下一个等价关系个数中减去从当前等价关系推出的个数即为当前不满足自反的二元组关系个数,直接推Bell三角形就可以
#include <cstdio>
#define ll long long
int const MAX = 4005;
int const MOD = 1e9 + 7;
ll dp[MAX][MAX];
int main()
{
int n;
scanf("%d", &n);
dp[0][0] = 1;
for(int i = 1; i <= n; i++)
{
dp[i][0] = dp[i - 1][i - 1];
for(int j = 1; j <= i; j++)
dp[i][j] = (dp[i][j - 1] + dp[i - 1][j - 1]) % MOD;
}
printf("%I64d
", dp[n][n - 1]);
}