agc035_e Develop

agc035_e Develop

https://atcoder.jp/contests/agc035/tasks/agc035_e

Tutorial

https://blog.csdn.net/qq_38609262/article/details/103058291

考虑被删除的数的集合(S)应该满足什么条件.

首先,显然只有([1,N])的数才可以被删除,然后应该存在某种(S)中元素顺序使得按这个顺序删除时不会写上任何数字.

考虑对于(x),向(x-2,x+K)连边,那么上面的条件相当于顶点集合(S)的诱导子图不存在环.此时拓扑序就是这个顺序.

注意向后的只有(x-2),所以考虑将([1,N])按奇偶分为两条链.

当(K)为偶数时,环只会出现在一条链上,相当于一条链上不能出现连续(dfrac K2)个被选的数.设(dp(i,j))表示现在在第(i)个点,接下来会有(j)个连续的点被选择.(O(n^2))即可.

当(K)为奇数时,环的形状如下

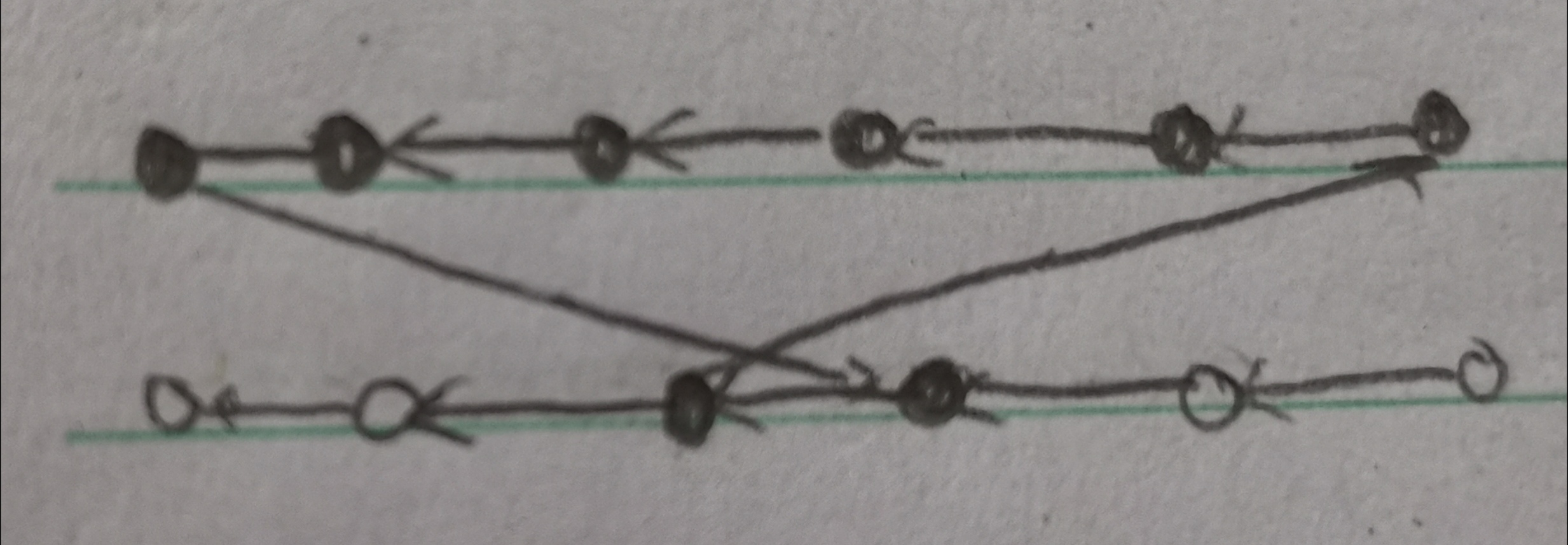
设(dp(i,j,k))表示现在已经考虑了奇链上前(i)个点和偶链上前(i+lfloor dfrac K2 floor)个点,奇链第(i)个点后会有连续(j)个点,偶链第(i+lfloor dfrac K2 floor)个点前有连续(k)个连续的点,转移时考虑两条链上接下来的点的状态,两个点可以同时加入(S)集合当且仅当不会出现上面那样的环.具体判断可参考代码,复杂度(O(n^3))

Code

#include <cstdio>
#include <cstring>
#include <iostream>
#define debug(...) fprintf(stderr,__VA_ARGS__)
using namespace std;
inline char gc() {
	return getchar();
	static char buf[100000],*l=buf,*r=buf;
	return l==r&&(r=(l=buf)+fread(buf,1,100000,stdin),l==r)?EOF:*l++;
}
template<class T> void rd(T &x) {
	x=0; int f=1,ch=gc();
	while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=gc();}
	while(ch>='0'&&ch<='9'){x=x*10-'0'+ch;ch=gc();}
	x*=f;
}
typedef long long ll;
const int MAXN=150+5;
int N,k,mod;
inline int add(int x) {return x>=mod?x-mod:x;}
inline void upd(int &x,int y) {x+=y; if(x>=mod) x-=mod;}
namespace sub0 {
	int dp[MAXN][MAXN];
	int sol(int n) {
		memset(dp,0,sizeof(dp));
		for(int i=0;i<=k;++i) dp[0][i]=1;
		for(int i=1;i<=n;++i) {
			int R=n-i+1;
			for(int j=1;j<=R;++j) upd(dp[i][j-1],dp[i-1][j]);
			for(int j=0;j<R&&j<=k;++j) upd(dp[i][j],dp[i-1][0]);
		}
		return dp[n][0];
	}
	int sol() {
		k>>=1;
		return (ll)sol(N>>1)*sol((N+1)>>1)%mod;
	}
}
namespace sub1 {
	int dp[MAXN][MAXN][MAXN];
	int sol() {
		int n=(N+1)>>1,m=N-n;
		k>>=1;
		for(int i=0;i<=n;++i) {
			dp[0][i][k]=1;
			for(int j=k-1,r=1;j>=0;--j) {
				dp[0][i][j]=r;
				r=add(r<<1);
			}	
		}
		for(int i=1;i+k<=m;++i) {
			int R=n-i+1;
			for(int j=1;j<=R;++j) for(int h=0;h<i+k;++h) if(dp[i-1][j][h]) {
				upd(dp[i][j-1][0],dp[i-1][j][h]);
				if(j+h<2*k+2) upd(dp[i][j-1][h+1],dp[i-1][j][h]);
			}
			for(int j=0;j<R;++j) for(int h=0;h<i+k;++h) if(dp[i-1][0][h]) {
				upd(dp[i][j][0],dp[i-1][0][h]);
				upd(dp[i][j][h+1],dp[i-1][0][h]);
			}
		}
		for(int i=m-k+1;i<=n;++i) {
			int R=n-i+1;
			for(int j=1;j<=R;++j) for(int h=0;h<=m;++h) if(dp[i-1][j][h]) {
				upd(dp[i][j-1][h],dp[i-1][j][h]);
			}
			for(int j=0;j<R;++j) for(int h=0;h<=m;++h) if(dp[i-1][0][h]) {
				upd(dp[i][j][h],dp[i-1][0][h]);
			}
		}
		int an=0;
		for(int h=0;h<=m;++h) upd(an,dp[n][0][h]);
		return an;
	}
}
int main() {
	rd(N),rd(k),rd(mod);
	if(~k&1) printf("%d
",sub0::sol());
	else printf("%d
",sub1::sol());
	return 0;
}