洛谷 P5280 [ZJOI2019]线段树
https://www.luogu.com.cn/problem/P5280


Tutorial
https://www.luogu.com.cn/blog/Sooke/solution-p5280
考虑一次修改中,每个节点的状态
(Sooke的图)
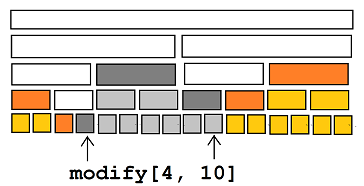
- dfs中经过的点(白)
- dfs的终点(黑)
- 白色的点的非黑白儿子(橙)
- 黑节点子树中的点(灰)
- 橙节点子树中的点(黄)
设(f(i,u))表示第(i)次修改后(u)节点在多少个线段树中的tag=1
首先对于所有点,在没有被修改的线段树中tag信息不会变化,接下来只考虑修改后的情况.
对于1类点,它的tag一定为0
对于2类点,它的tag一定为1
对于3类点,它的tag是否为1取决于它到根的路径上是否有节点的tag=1.
所有我们需要额外维护一个信息,设(g(i,u))表示第(i)次修改后在多少个线段树中(u)到根的路径上的节点的tag都为0
(败者食尘)
对于1类点,它的tag一定为0,它到根的路径上的tag都为0
g[u]+=power(2,i-1);
对于2类点,它的tag一定为1
f[u]+=power(2,i-1);
对于3类点,它的tag是否为1取决于它到根的路径上是否有节点的tag=1
f[u]+=(power(2,i-1)-g[u]);
g[u]+=g[u];
对于4类点,它的tag不会变化,它到根的路径上一定有一个2类点tag=1
f[u]+=f[u]
对于5类点,它的tag不会变化,它到根的路径上是否有节点tag=1的情况不会变化
f[u]+=f[u];
g[u]+=g[u];
1,2,3类点的数量为(O(log n)),可以在dfs过程中维护
4,5类点相当于将子树内的值全部乘2,可以用lazy标记维护
额外维护(sf(u))表示(u)子树中(f)的和.询问答案为(sf(1))
Code
#include <cstdio>
#include <iostream>
#define debug(...) fprintf(stderr,__VA_ARGS__)
#define lson u<<1,l,mid
#define rson u<<1|1,mid+1,r
using namespace std;
inline char gc() {
// return getchar();
static char buf[100000],*l=buf,*r=buf;
return l==r&&(r=(l=buf)+fread(buf,1,100000,stdin),l==r)?EOF:*l++;
}
template<class T> void rd(T &x) {
x=0; int f=1,ch=gc();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=gc();}
while(ch>='0'&&ch<='9'){x=x*10-'0'+ch;ch=gc();}
x*=f;
}
typedef long long ll;
const int mod=998244353;
const int maxn=1e5+50,maxm=1e5+50;
int n,m;
int cnt;
int pow2[maxm];
inline int add(int x) {return x>=mod?x-mod:x;}
inline int sub(int x) {return x<0?x+mod:x;}
namespace seg {
const int maxnode=maxn<<3;
int f[maxnode],sf[maxnode],tagf[maxnode];
int g[maxnode],tagg[maxnode];
inline void changeg(int u,int d) {
g[u]=(ll)g[u]*d%mod;
tagg[u]=(ll)tagg[u]*d%mod;
}
inline void changef(int u,int d) {
f[u]=(ll)f[u]*d%mod,sf[u]=(ll)sf[u]*d%mod;
tagf[u]=(ll)tagf[u]*d%mod;
}
inline void pushdown(int u) {
if(tagf[u]!=1) {
changef(u<<1,tagf[u]);
changef(u<<1|1,tagf[u]);
tagf[u]=1;
}
if(tagg[u]!=1) {
changeg(u<<1,tagg[u]);
changeg(u<<1|1,tagg[u]);
tagg[u]=1;
}
}
inline void pushup(int u) {
sf[u]=add(f[u]+add(sf[u<<1]+sf[u<<1|1]));
}
inline void change5(int u) {
changef(u,2),changeg(u,2);
}
inline void change4(int u) {
changef(u,2);
}
inline void change3(int u) {
f[u]=add(sub(pow2[cnt-1]-g[u])+f[u]);
g[u]=add(g[u]<<1);
pushdown(u);
change5(u<<1),change5(u<<1|1);
pushup(u);
}
inline void change2(int u) {
f[u]=add(pow2[cnt-1]+f[u]);
}
inline void change1(int u) {
g[u]=add(pow2[cnt-1]+g[u]);
}
void build(int u,int l,int r) {
g[u]=1;
tagf[u]=tagg[u]=1;
if(l==r) {
return;
}
int mid=(l+r)>>1;
build(lson);
build(rson);
pushup(u);
}
void update(int u,int l,int r,int ql,int qr) {
if(l==ql&&r==qr) {
change2(u);
pushdown(u);
change4(u<<1),change4(u<<1|1);
pushup(u);
return;
}
int mid=(l+r)>>1;
change1(u);
pushdown(u);
if(qr<=mid) {
change3(u<<1|1);
update(lson,ql,qr);
}
else if(ql>mid) {
change3(u<<1);
update(rson,ql,qr);
}
else {
update(lson,ql,mid);
update(rson,mid+1,qr);
}
pushup(u);
}
}
void init() {
pow2[0]=1;
for(int i=1;i<=m;++i) pow2[i]=add(pow2[i-1]<<1);
}
int main() {
rd(n),rd(m);
init();
seg::build(1,1,n);
for(int i=1;i<=m;++i) {
int op; rd(op);
if(op==1) {
int l,r; rd(l),rd(r);
++cnt,seg::update(1,1,n,l,r);
}
else {
printf("%d
",seg::sf[1]);
}
}
return 0;
}