Generalized linear models with nonlinear feature transformations (特征工程 + 线性模型) are widely used for large-scale regression and classification problems with sparse inputs. Memorization of feature interactions (线性模型中学习到的特征系数解释性强)through a wide set of cross-product feature transformations are effective and interpretable, while generalization requires more feature engineering effort(线性模型的泛化性能需要大量的特征工程).
With less feature engineering, deep neural networks can generalize better to unseen feature combinations through low-dimensional dense embeddings learned for the sparse features. (dnn从稀疏的特征向量中学习得到低维度词向量,泛化性能较好,但是可能欠拟合)However, deep neural networks with embeddings can over-generalize。
Wide & Deep learning—jointly trained wide linear models and deep neural networks—to combine the benefits of memorization and generalization for recommender systems.

The Wide Component
The wide component is a generalized linear model of the form $y = w^T x + b$, as illustrated in Figure 1 (left). y is the prediction, $x = [x_1, x_2, ..., x_d] $ is a vector of d features, $w = [w_1, w_2, ..., w_d]$ are the model parameters and b is the bias. The feature set includes raw input features and transformed features(比如组合特征).
The Deep Component
The deep component is a feed-forward neural network, as shown in Figure 1 (right). For categorical features, the original inputs are feature strings (e.g., “language=en”). Each of these sparse, high-dimensional categorical features are first converted into a low-dimensional and dense real-valued vector(有两种处理办法,一种是对每个field的特征进行embedding得到一个词向量,一种是所有field特征都one-hot后再经由一个embedding层后得到一个词向量,这里采用后者), often referred to as an embedding vector. The dimensionality of the embeddings are usually on the order of O(10) to O(100). The embedding vectors are initialized randomly and then the values are trained to minimize the final loss function during model training. These low-dimensional dense embedding vectors are then fed into the hidden layers of a neural network in the forward pass. Specifically, each hidden layer performs the following computation:
$a ^{(l+1)} = f(W^{(l)} a ^{(l)} + b^ {(l)} )$
where l is the layer number and f is the activation function, often rectified linear units (ReLUs). $a^{(l)} , b^{(l)} , and W^{(l)} $ are the activations, bias, and model weights at l-th layer.
Joint Training of Wide & Deep Model
The wide component and deep component are combined using a weighted sum of their output log odds as the prediction, which is then fed to one common logistic loss function for joint training(Wide部分和deep部分都输出一个概率,然后加权平均(权值需要学习),加权平均后得到的概率可直接用于对数损失函数,其实就是LR). (paddle中的实现:concatenate LR和DNN的输出,得到一个二维向量,经由一个全连接层(激活函数为sigmoid),输出最终概率。其实和前面的注释意义一样)Note that there is a distinction between joint training and ensemble. In an ensemble, individual models are trained separately without knowing each other, and their predictions are combined only at inference time but not at training time. In contrast, joint training optimizes all parameters simultaneously by taking both the wide and deep part as well as the weights of their sum into account at training time. For joint training the wide part only needs to complement the weaknesses of the deep part with a small number of cross-product feature transformations, rather than a full-size wide model.
Joint training of a Wide & Deep Model is done by backpropagating the gradients from the output to both the wide and deep part of the model simultaneously using mini-batch stochastic optimization. In the experiments, we used Followthe-regularized-leader (FTRL) algorithm [3] with L1 regularization as the optimizer for the wide part of the model, and AdaGrad [1] for the deep part(Wide部分使用FTRL优化算法即sgd+L1正则,Deep部分使用AdaGrad优化算法,但是paddle中对于一个Model只能指定一个优化方法).
The combined model is illustrated in Figure 1 (center). For a logistic regression problem, the model’s prediction is:
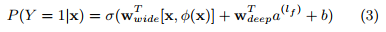
where Y is the binary class label, σ(·) is the sigmoid function, φ(x) are the cross product transformations of the original features x, and b is the bias term. $w_{wide}$ is the vector of all wide model weights, and $w_{deep}$ are the weights applied on the final activations $a^{(lf)}$ .
 实际项目中,Deep部分的输入为类别特征,需要进行one-hot处理,Wide部分其实就是一个LR,使用统计特征,cvr特征等,统计特征进行one-hot处理,cvr特征需要离散化再one-hot处理。
实际项目中,Deep部分的输入为类别特征,需要进行one-hot处理,Wide部分其实就是一个LR,使用统计特征,cvr特征等,统计特征进行one-hot处理,cvr特征需要离散化再one-hot处理。
搭建网络:
class CTRmodel(object): ''' A CTR model which implements wide && deep learning model. ''' def __init__(self, dnn_layer_dims, dnn_input_dim, lr_input_dim, model_type=ModelType.create_classification(), is_infer=False): ''' @dnn_layer_dims: list of integer dims of each layer in dnn @dnn_input_dim: int size of dnn's input layer @lr_input_dim: int size of lr's input layer @is_infer: bool whether to build a infer model ''' self.dnn_layer_dims = dnn_layer_dims self.dnn_input_dim = dnn_input_dim self.lr_input_dim = lr_input_dim self.model_type = model_type self.is_infer = is_infer self._declare_input_layers() self.dnn = self._build_dnn_submodel_(self.dnn_layer_dims) self.lr = self._build_lr_submodel_() # model's prediction # TODO(superjom) rename it to prediction if self.model_type.is_classification(): self.model = self._build_classification_model(self.dnn, self.lr) if self.model_type.is_regression(): self.model = self._build_regression_model(self.dnn, self.lr) # layer.data: define DataLayer For NeuralNetwork. def _declare_input_layers(self): # Deep部分的输入,使用类别特征,需要one-hot处理 # Sparse binary vector : the input feature is a sparse vector and the every element in this vector is either zero or one.
# sparse_binary_vector的输入是特征值的下标组成的向量 self.dnn_merged_input = layer.data( name='dnn_input', type=paddle.data_type.sparse_binary_vector(self.dnn_input_dim)) # Wide部分的输入,使用统计特征和cvr特征等,统计特征one-hot处理,cvr特征先离散化再one-hot # Sparse vector : the input feature is a sparse vector. Most of the elements in this vector are zero, others could be any float value. # sparse_vector的输入是(index:value)元素组成的向量
self.lr_merged_input = layer.data( name='lr_input', type=paddle.data_type.sparse_vector(self.lr_input_dim)) # 二分类模型学习的标签 # Dense Vector : the input feature is dense float vector. if not self.is_infer: self.click = paddle.layer.data( name='click', type=dtype.dense_vector(1)) # Deep部分使用了标准的多层前向传导的 DNN 模型,这里输入的特征都作了one-hot处理,然后作为一个整体进行embedding,得到词向量。
# DeepFM对每个field单独进行embedding,有多个embedding层 # 注意使用的时候dnn_layer_dims = [128, 64, 32, 1] def _build_dnn_submodel_(self, dnn_layer_dims): ''' build DNN submodel. ''' dnn_embedding = layer.fc( input=self.dnn_merged_input, size=dnn_layer_dims[0]) _input_layer = dnn_embedding for i, dim in enumerate(dnn_layer_dims[1:]): fc = layer.fc( input=_input_layer, size=dim, act=paddle.activation.Relu(), name='dnn-fc-%d' % i) _input_layer = fc return _input_layer # Wide部分,直接使用LR模型,激活函数改为RELU来加速. def _build_lr_submodel_(self): ''' config LR submodel ''' # size是layer dimension,我的理解是layer中神经元数目 fc = layer.fc( input=self.lr_merged_input, size=1, act=paddle.activation.Relu()) return fc # 融合Wide和Deep部分 def _build_classification_model(self, dnn, lr): merge_layer = layer.concat(input=[dnn, lr]) # sigmoid输出概率 self.output = layer.fc( input=merge_layer, size=1, # use sigmoid function to approximate ctr rate, a float value between 0 and 1. act=paddle.activation.Sigmoid()) if not self.is_infer: # multi_binary_label_cross_entropy_cost: a loss layer for multi binary label cross entropy # 分类问题使用交叉熵损失 self.train_cost = paddle.layer.multi_binary_label_cross_entropy_cost( input=self.output, label=self.click) return self.output def _build_regression_model(self, dnn, lr): merge_layer = layer.concat(input=[dnn, lr]) self.output = layer.fc( input=merge_layer, size=1, act=paddle.activation.Sigmoid()) if not self.is_infer: # 回归问题使用mse损失 self.train_cost = paddle.layer.mse_cost( input=self.output, label=self.click) return self.output
训练模型:
dnn_layer_dims = [128, 64, 32, 1] # ============================================================================== # cost and train period # ============================================================================== def train(): args = parse_args() args.model_type = ModelType(args.model_type) paddle.init(use_gpu=False, trainer_count=1) dnn_input_dim, lr_input_dim = reader.load_data_meta(args.data_meta_file) # create ctr model. model = CTRmodel( dnn_layer_dims, dnn_input_dim, lr_input_dim, model_type=args.model_type, is_infer=False) # Parameters is a dictionary contains Paddle’s parameter,输入是网络的cost layer params = paddle.parameters.create(model.train_cost) optimizer = paddle.optimizer.AdaGrad() trainer = paddle.trainer.SGD( cost=model.train_cost, parameters=params, update_equation=optimizer) dataset = reader.Dataset() def __event_handler__(event): if isinstance(event, paddle.event.EndIteration): num_samples = event.batch_id * args.batch_size if event.batch_id % 100 == 0: logger.warning("Pass %d, Samples %d, Cost %f, %s" % ( event.pass_id, num_samples, event.cost, event.metrics)) if event.batch_id % 1000 == 0: if args.test_data_path: result = trainer.test( reader=paddle.batch( dataset.test(args.test_data_path), batch_size=args.batch_size), feeding=reader.feeding_index) logger.warning("Test %d-%d, Cost %f, %s" % (event.pass_id, event.batch_id, result.cost, result.metrics)) path = "{}-pass-{}-batch-{}-test-{}.tar.gz".format( args.model_output_prefix, event.pass_id, event.batch_id, result.cost) with gzip.open(path, 'w') as f: params.to_tar(f) trainer.train( # shuffle: 每次读入buffer_size条训练数据到一个buffer里,然后随机打乱其顺序,并且逐条输出 # 一个batched reader每次yield一个minibatch # num_passes : The total train passes. # feeding (dict|list) : Feeding is a map of neural network input name and array index that reader returns. reader=paddle.batch( paddle.reader.shuffle( dataset.train(args.train_data_path), buf_size=500), batch_size=args.batch_size), feeding=reader.feeding_index, event_handler=__event_handler__, num_passes=args.num_passes)
调参
初始化参数:
默认情况下,PaddlePaddle使用均值0,标准差为$(frac{1}{sqrt{d}})$ 来初始化参数。其中$d$ 为参数矩阵的宽度。这种初始化方式在一般情况下不会产生很差的结果。如果用户想要自定义初始化方式,PaddlePaddle目前提供两种参数初始化的方式(在定义layer的时候设置参数的初始化方式):
- 高斯分布。将
param_attr设置成param_attr=ParamAttr(initial_mean=0.0, initial_std=1.0) - 均匀分布。将
param_attr设置成param_attr=ParamAttr(initial_max=1.0, initial_min=-1.0)
paddle中fc层的参数有:

调整学习率:


上述在定义
optimizer = paddle.optimizer.AdaGrad()
的时候可以指定相关参数。
adam_optimizer = paddle.optimizer.Adam( learning_rate=1e-3, regularization=paddle.optimizer.L2Regularization(rate=1e-3), model_average=paddle.optimizer.ModelAverage(average_window=0.5))
http://www.datakit.cn/blog/2016/08/21/wdnn.html
Using pre-trained word vectors in embedding layer:
https://github.com/PaddlePaddle/Paddle/issues/490
paddle实现推荐系统:
http://book.paddlepaddle.org/index.cn.html