dp算法之有代价的最短路径

题目：有代价的最短路径

题目介绍：如下图所示，现在平面上有N个点，此时N=7，每个点可能和其他点相连，相连的线有一定权值，求出从0点到N-1点的消耗权值的最小值。

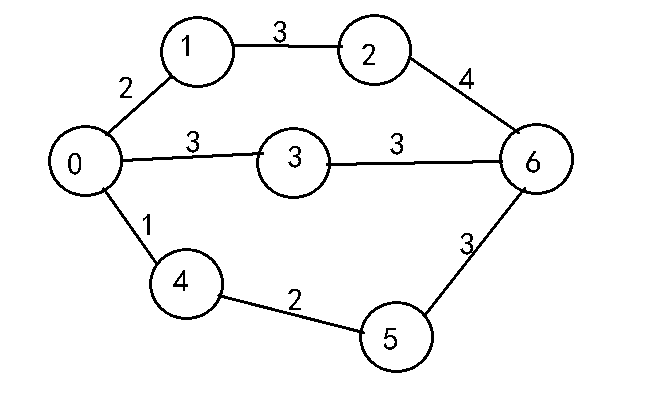
分析：用动态规划的思路来解决，每一点与其他点的消耗权值的最小值都储存在一个二维数组中，下一个点消耗的最小值可以根据前一个点来得出。如果两个点不相连，可以认为这两点的权值为无穷大。设一个二维数组初始化为无穷，再导入权值初始值，再用状态方程得出最小值储存在数组中。

状态方程：l[k][j] = min(l[k][j], l[k][i] + l[i][j])

我们可以得出0到N-1的最短路径表格：

距离	0	1	2	3	4	5	6
0	0	2	5	3	1	3	6

代码：

#include <iostream>
using namespace std;
int min(int a, int b);
int main()
{
    int X = 99999;
    int N = 7;
    int i, j, k;
    int **l = new int *[N];
    for (i = 0; i<N; i++)
    {
        l[i] = new int[N];
    }
    for (i = 0; i < N; i++)
    {
        for (j = 0; j < N; j++)
        {
            l[i][j] = X;
        }
    }
    l[0][1] = l[1][0] = 2;
    l[1][2] = l[2][1] = 3;
    l[2][6] = l[6][2] = 4;
    l[0][3] = l[3][0] = 3;
    l[3][6] = l[6][3] = 3;
    l[0][4] = l[4][0] = 1;
    l[4][5] = l[5][4] = 2;
    l[5][6] = l[6][5] = 3;
    for (k = 0; k < N; k++)
    {
        for (j = 0; j < N; j++)
        {
            for (i = 0; i < N; i++)
            {
                l[k][j] = min(l[k][j], l[k][i] + l[i][j]);
            }
        }
    }
    for (i = 1; i < N; i++)
    {
        cout << l[0][i] << endl;
    }
}
int min(int a, int b)
{
    if (a > b)
    {
        return b;
    }
    else { return a; }
}

结果：