数据分析,先有数据,而后有分析,认识数据是分析数据的前提。在现实世界中,数据一般都是有缺失的、异构的、有量纲的。认识数据,不仅要了解数据的属性(维)、类型和量纲,还要了解数据的分布特性。洞察数据的特征,检验数据的质量,有助于后续的分析工作,否则,没有可信的数据,数据分析的结果将是空中楼阁。
一,检验数据质量
你不能想当然地认为数据是有效的,有些数据是从多个不同的数据源中获取的,这些异构数据,在各自的系统中都是正确无误的,只不过很有“个性”,例如,有的系统中使用0和1,代表性别;而有些系统使用f和m代表性别,因此,在使用数据之前,首先要对数据做集成处理,使用一致的单位、使用统一的文本来描述对象等。有些数据中包含大量重复的数据、包含缺失的数据、或者包含离群的数据,在开始分析数据之前,必须好好检查数据是否有效,并对数据做预处理操作。判断离群数值,并对其分析,有时会导致重大发现的产生。
二,识别定性和定量属性
观测(observation)是一个数据对象,对应于数据表的一行,表示一个属性组的观测值。属性(attribute)是一个数据字段,表示数据对象的一个特征。在数据分析中,属性、维(Dimension)、特征(feature)和变量(Variable)可以互换使用,按照属性值功能的不同,可以把属性分位定性属性和定量属性。
(1)定性属性是指用文本描述对象的特征,定性属性主要分为三类:
- 标称属性:也叫做类别属性,用于对数据对象分类(Category),比如,头发的颜色、职业
- 二元属性:只有两个类别的属性,如果二元属性的两种状态具有同等价值或具有相同的权重,那么认为该二元属性是对称的,例如,性别;非对称是指两种状态的结果不是同样重要的,例如,是否吸烟对治疗的效果而言,其权重是不同的。
- 序数属性:属性的顺序是有意义的,通常用于等级评定。通常情况下,序数属性是定性的文本,比如,官职、消费者满意度,但是,序数属性也可以通过把数值属性分割成不同的区间来得到,比如,年龄段。
在序数属性中,有一类重要的属性,叫做时间属性,一些常见的分析方法,比如时序分析,周期性分析等都是基于时间属性的。
(2)定量属性是指用数值描述对象,可以比较大小,是可以量化的属性,定量属性主要分为两个标度:
- 区间标度:可度量的数值,用整数或实数表示,比如,年纪、薪水
- 比率标度:比例数值,比如,速度、留存率
定量属性通常含有量纲,例如,身高的量纲是cm,而薪水的量纲是元,同一量纲的数据可以比较大小,不同量纲的数据,需要通过归一化去量纲之后,比较大小才有意义。定性数据通常是分析数据的一个角度,增加维度,从不同的角度来看待问题,能够细分指标,增加分析的深度。
三,查看数据的基本统计描述
统计是数据分析的好助手,查看数据集的基本统计描述,能够帮助我们了解数据的全貌,识别数据的分布特征。由于定量数据天生具有计算的特性,数据的分布通常是针对定量数据进行的统计描述。基本统计描述主要是指从数据的集中趋势、离散趋势和分布来认识数据。每个统计描述,都使用特定的统计量来衡量。
1,集中趋势
数据的集中趋势,用于度量数据分布的中心位置,直观地说,测量一个属性值的大部分落在何处。描述数据集中趋势的统计量是:均值、中位数、众数。
- 均值(mean)是数据的算术平均值,是描述数据集的中心位置时最常用的统计量,但是,均值对离群值很敏感。
- 中位数(median)是有序数据值的中间值,它把数据分为两半,一端是较高的一半,另一端是较低的一半。当数据中出现极端值时,中位数是比均值更好地度量数据中心的统计量。
- 众数(mode)是数据中出现次数最多的值,一般用于定性数据。
了解数据的集中趋势,能够避免做出错误的统计分析,说一个真实的谎言,每当国家统计局公布人均工资水平时,总会在社会上引起不小的反响,很多人都感概被富裕了,这是因为贫富差距太大,导致平均工资不能刻画人均收入的平均水平。这种情况下,可以使用中位数来表示人均工资,或者使用其他的指标,比如基尼系数。
2,离散趋势
数据的离散趋势,用于描述数据的分散程度,描述离散趋势的统计量是:值域、四分位数极差(IQR)、标准差、变异系数
- 值域(Range)是数据中的最大值和最小值的差,反映数据的波动范围
- 内距(IQR,Inter-Quartile Range),又称作四分位数极差,是上四分位数和下四分位数的差值,给出数据的中间一半所覆盖的范围
- 标准差:计算所有数值相对均值的偏离量,反映数据在均值附近的波动程度
通过测定数据的离散程度,可以反映观测值之间的差异大小,从而评估分布中心的指标对各个观测变量值代表性的高低。平均工资之所以不能刻画人均收入的平均水平,一个很大的原因是工资的离散程度太大。
3,数据的分布
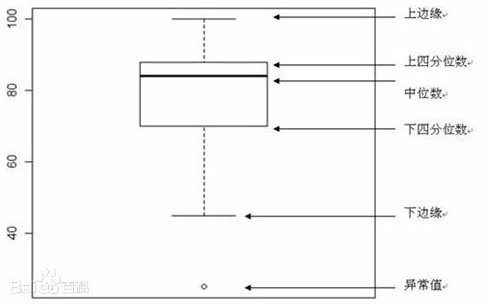
数据的分布,统计量只能衡量总体数据的集中和离散程度,而分位数却能直观地描述数据的分布。使用分位数来表示数据的分布,通常使用五箱图(box plot)来可视化,它不仅能够呈现数据的分布,而且可以呈现离群点的分布,如下图。
箱图识别可以的离群点的规则是:挑选落在Q3之上或Q1之下至少1.5*IQR处的值。
分位数是观察数据分布的最简单有效的方法,但分位数只能用于观察单一属性的数据分布。散点图可以用来观察双变量的数据分布,聚类可以用来观察更多变量的数据分布。
通过观察数据的分布,采用合理的指标,使数据的分析更全面,避免得出像平均工资这类偏离事实的的分析结果。
四,归一化
属性的值,有时是有单位的,称作量纲数据。不同评价指标往往具有不同的量纲,数据之间的差别可能很大,不进行处理会影响到数据分析的结果。为了消除指标之间的量纲和取值范围差异对数据分析结果的影响,需要对数据进行标准化处理,就是说,把数据按照比例进行缩放,使之落入一个特定的区域,便于进行综合分析。
(1)所谓量纲,简单来说,就是说数据的单位;有些数据是有量纲的,比如身高,而有些数据是没有量纲的,例如,男女比例。无量纲化,是指去除数据的单位限制,将其转化为无量纲的纯数值,便于不同单位或者量级的指标能够进行和加权。
(2)数据的标准化是指将数据按照比例缩放,使之落入一个特定的区间。
(3)归一化是数据标准化中最简单的方式,目的是把数变为(0,1)之间的小数,把有量纲的数据转换为无量纲的纯数量。
归一化能够避免值域和量纲对数据的影响,便于对数据进行综合分析,举个简单的例子,在一次考试中,小明的语文成绩是100分、英语成绩是100分,单单从这考试成绩来评价,小明的语文和英语学的一样好。但是,如果你知道语文总分是150分,而英语总分只有120分,你还认为小明的语文和英语成绩是一样的吗?
对小明的成绩做简单的归一化:采用离差归一化方法,公式是:y = (x-min) / range,这里设min=0,那么 range = max - min = max,由此推算出小明的语文成绩是4/6,英语成绩是5/6,因此,判定小明的英语成绩好于语文成绩。
还原到真实的场景中,各科的考题难度不尽相同,设班级中语文的最低分数是min语文 = 60,英语的最低分数是min英语 = 85,推算出小明的语文成绩是0.44 =(100-60)/(150-60),英语成绩是0.43 = (100-85)/(120-85),据此,可以判断小明的英语成绩稍差于语文成绩。
归一化的使得具有不同值域、不同量纲的数据之间具有可比性,使数据分析的结果更加全面,更接近事实。
参考文档:
数据挖掘的概念与技术