数据分析 第三篇：数据特征分析（分布+帕累托+周期）

在数据质量得到保证的前提下，通过绘制图表、计算某些统计量等手段对数据的分布特征和贡献度进行分析（帕累托分析），分布分析能够揭示数据的分布特征和分布类型，对于定量数据，可以做出频率分布表、绘制频率分布直方图显示分布特征；对于定性数据，可用饼图和条形图显示分布情况。帕累托分析在频率分布直方图的基础上，绘制累积频率，计算投入的效益。

下面的例子使用vcd包中的Arthritis数据集来做数据的分布分析和帕累托分析。

 library(grid)
 library(vcd)
 head(Arthritis)

  ID Treatment  Sex Age Improved
1 57   Treated Male  27     Some
2 46   Treated Male  29     None
3 77   Treated Male  30     None
4 17   Treated Male  32   Marked
5 36   Treated Male  46   Marked
6 23   Treated Male  58   Marked

一，定量数据的分布分析

对于定量数据，做频率分布表，绘制频率分布直方图。选择“组数”和“组宽”是做频率分布分析时遇到的最主要问题，一般按照以下5个步骤来实现：

• 求值域（range）：值域 = 最大值 - 最小值
• 决定组距和组数：组距是每个区间的长度，组数 = 值域 /  组距
• 决定组限： 组限是指每个区间的端点，这一步是要确定每组的起点和终点
• 列出频率分布表
• 绘制频率分布直方图

在进行分组时，应遵循的主要原则有：

• 各组之间是互斥的
• 各组的组距相等

（1）制作频率分布表

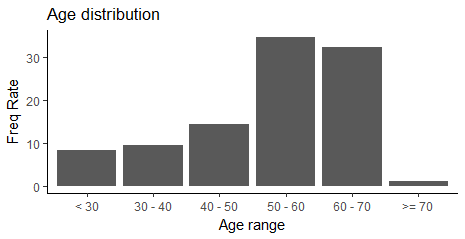
按照年龄段来计算频数，每10年为一个年龄段，统计各个年龄段的人数。由于Arthritis数据集中并没有该分类变量，这就需要自定义区间，按照分组的间隔来制作频数分布表。频率分布表的制作过程在文章《R实战 第九篇：列联表和频数表》中有详细的描述，不再赘述。

library(grid)
library(vcd)

labels <- c("< 30", "30 - 40", "40 - 50", "50 - 60", "60 - 70", ">= 70")
breaks <- c(1,30,40,50,60,70,100)
mytable <- cut(Arthritis$Age, breaks = breaks, labels = labels, right = TRUE )
df <- as.data.frame(table(Age=mytable))

df <- transform(df, cumFreq = cumsum(Freq), FreqRate = prop.table(Freq))
df <- transform(df, CumFreqRate= cumsum(FreqRate))
df <- transform(df,FreqRate=round(FreqRate * 100,2), CumFreqRate= round(CumFreqRate*100,2))

（2）绘制频率分布直方图

使用ggplot绘制频率分布直方图：

ggplot(data=df, mapping=aes(x=factor(Age),y=FreqRate,group=factor(Age))) +
  geom_bar(stat="identity")+
  labs(title='Age distribution',x='Age range',y='Freq Rate')+
  theme_classic()

二，定性数据的分布分析

对于定性变量，通常根据分类来分组，然后统计分组的频数或频率，可以采用饼图或条形图来描述定性数据的分布：

• 饼图的每一个扇形部分代表每一类型的百分比或频数，根据定性变量的类型把饼图分成几个部分，每一个部分的大小与每一个类型的频数成正比；
• 条形图的高度代表每一类型的百分比或频数，条形图的宽度没有意义。

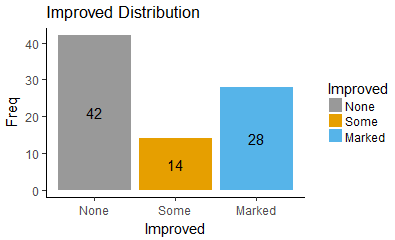
按照Improved变量的频数来绘制饼图和条形图：

mytable <- with(Arthritis, table(Improved))
df <- as.data.frame(mytable)

1，绘制条形图

使用geom_bar绘制条形图：

ggplot(data=df,mapping = aes(x=Improved, y=Freq,fill=Improved)) +
  geom_bar(stat="identity")+
  scale_fill_manual(values=c("#999999", "#E69F00", "#56B4E9"))+
  labs(title='Improved Distribution', x='Improved',y='Freq')+
  geom_text(stat="identity",aes(y=Freq, label = Freq), size=4, position=position_stack(vjust = 0.5))+
  theme_classic()

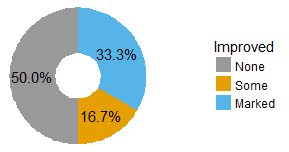
2，绘制饼图

使用geom_bar()和 coord_polar() 函数来绘制饼图，通常情况下，饼图显示的是百分比，而直方图显示的某个分类的具体数值：

blank_theme <- theme_minimal()+
  theme(
    axis.title.x = element_blank(),
    axis.title.y = element_blank(),
    axis.text.x = element_blank(),
    axis.text.y = element_blank(),
    panel.border = element_blank(),
    panel.grid=element_blank(),
    axis.ticks = element_blank(),
    plot.title=element_text(size=14, face="bold")
  )

ggplot(data=df, mapping=aes(x="Improved",y=Freq,fill=Improved))+
  geom_bar(stat="identity",width=0.5,position='stack',size=5)+
  coord_polar("y", start=0)+
  scale_fill_manual(values=c("#999999", "#E69F00", "#56B4E9"))+
  blank_theme +
  geom_text(stat="identity",aes(y=Freq, label = scales::percent(Freq/sum(Freq))), size=4, position=position_stack(vjust = 0.5))

三，帕累托分析

帕累托分析依据的原理是20/80定律，80%的效益常常来自于20%的投入，而其他80%的投入却只产生了20%的效益，这说明，同样的投入在不同的地方会产生不同的效益。

怕累托图的绘制过程是按照贡献度从高到低依次排列，并绘制累积贡献度曲线。当样本数量足够大时，贡献度通常会呈现20/80分布。

使用ggplot2绘制的帕累托图的脚本和图如下所示：

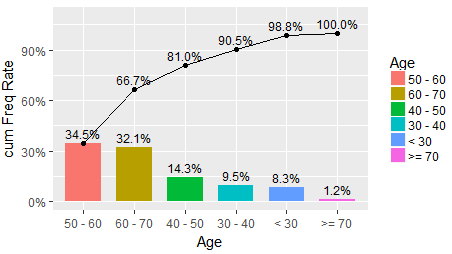
library(grid)
library(vcd)
library(ggplot2)
library(scales)

labels <- c("< 30", "30 - 40", "40 - 50", "50 - 60", "60 - 70", ">= 70")
breaks <- c(1,30,40,50,60,70,100)
mytable <- cut(Arthritis$Age, breaks = breaks, labels = labels, right = TRUE )
df <- as.data.frame(table(Age=mytable),stringsAsFactors=FALSE)
df <- transform(df, FreqRate = prop.table(Freq))

df <- df[order(df$Freq,decreasing =TRUE),]
rownames(df) <- seq(nrow(df))
df$Age <- factor(df$Age,levels=df$Age)
df$cumRate <- cumsum(df$FreqRate)
df$cumRateLable <- as.character(percent(df$cumRate))

df$cumRateLable[1] <- ""

ggplot(df, aes(x=Age,y=FreqRate,fill=Age)) +
  geom_bar(stat="identity",width = 0.7) +
  geom_text(stat='identity',aes(label=percent(FreqRate)),vjust=-0.5, color="black", size=3)+
  scale_y_continuous(name="cum Freq Rate",limits=c(0, 1.1),labels = function(x) paste0(x*100, "%"))+
  geom_point(aes(y=cumRate),show.legend=FALSE) +
  geom_text(stat="identity",aes(label=cumRateLable,y=cumRate), vjust=-0.5, size=3)+
  geom_path(aes(y=cumRate, group=1))

四，周期性分析

周期性分析是探索某个变量是否随着时间变化而呈现出某种周期性变化的趋势，时间尺度的选择有年度、季度、月份、周度、天和小时等时间周期。

在进行周期性分析时，不能简单地以天或月来对数据进行分析，因为，在大多数情况下，人们都是在周一到周五工作，在周六和周日休息，所以，应该根据用户的行为习惯和业务场景，选择合适的时间尺度。结合笔者的工作经验，最常用的周期是周。

对于消费行业数据，节假日是一个必须要考虑的时间点，比如，法定节假日、双11、618等，还有周末，对于这样的时间点，数据量会增加很多，没有节假日和有节假日，数据的差距是非常大的。

对于某些数据，这些特殊的时间点不一定带来数据的暴增，例如，对于一些技术类网站，由于人们只在工作日访问，因此访问量在工作日明显增大，而在周末、或节假日则会明显降低。对于这些特殊的时间点，在分析数据时，应考虑周全，特殊处理。

参考文档：