探索数据是指研究数据,发现数据的结构。数据集由数据对象构成,一个数据对象代表一个实体,实体由属性构成,属性是一个数据字段,表示数据对象的一个特征,通常,在数据分析和机器学习中,属性、维度、特征和变量这四个术语可以互换。
用来描述一个数据对象的一组属性,称作属性向量或者特征向量。一个属性的类型是由该属性的值决定的,属性可以是标称的、二元的、序数的和数值的。
本文使用的数据,使用以下脚本获得,案例是预测某个区域的房价,本文重点关注的是如何探索数据和对数据进行预处理。

import os import tarfile import urllib import pandas as pd DOWNLOAD_ROOT = "https://raw.githubusercontent.com/ageron/handson-ml2/master/" HOUSING_PATH = os.path.join("datasets", "housing") HOUSING_URL = DOWNLOAD_ROOT + "datasets/housing/housing.tgz" def fetch_housing_data(housing_url=HOUSING_URL, housing_path=HOUSING_PATH): if not os.path.isdir(housing_path): os.makedirs(housing_path) tgz_path = os.path.join(housing_path, "housing.tgz") urllib.request.urlretrieve(housing_url, tgz_path) housing_tgz = tarfile.open(tgz_path) housing_tgz.extractall(path=housing_path) housing_tgz.close() def load_housing_data(housing_path=HOUSING_PATH): csv_path = os.path.join(housing_path, "housing.csv") return pd.read_csv(csv_path) #get data fetch_housing_data() housing = load_housing_data()
快速查看数据的结构,每一行代表一个区域,共有10个属性,其中median_house_value是需要预测的属性值。
housing.head()

一,属性
属性可以分为两大类:定性属性和定量属性,还可以把属性分为离散属性和连续属性。
1,定性属性和定量属性
定性属性:
- 标称属性:属性的值代表类别、编码或状态,因此标称属性被看作是分类属性。
- 二元属性:属性只有两个类别或状态,0和1
- 序数属性:属性值之间存在有意义的顺序,比如成绩等级可以分为:差、良、优,
定量属性是定量的,它的值是可度量的,用整数或实数来表示,定量属性分为标量和比率。
- 数量属性:标量数值,比如成绩、温度、销量等
- 比率属性:表示一个值是另一个的倍数(或比率),比如,增长率、占比等。
2,离散属性和连续属性
离散属性是指存在有限个值,或可数的值
连续属性:值的个数是不可数的
3,对housing数据按照属性进行分析
housing数据共有10个属性,其中9个属性属于标量属性,1个标称属性。
标量属性:
- longitude 和 latitude:表示区域的经纬度,
- housing_median_age :表示房龄中位数
- total_rooms:区域中的总房间数量
- total_bedrooms:区域中的总卧室数量
- population:区域中的人口数量
- households:区域中的家庭数量
- median_income :区域中的人口收入中位数
标称属性:
- ocean_proximity:近海
预测值是标量值:
- median_house_value:房屋价值中位数
二,数据的基本统计描述
数据的基本统计描述,是对数据集的整体做一个统计描述,通常是对一个属性进行统计分析。
1,总体数量统计
值的数量、唯一值的数量
2,缺失值
属性字段是否存在缺失值
3,中心趋势分析
- 均值
- 中位数
- 众数
4,离中趋势分析
值域:最小值和最大值之间的差值
方差和标准差:对同一值域的属性来说,标准差越大,数据的离散程度越大
四分位数:箱线图分析,特别是四分位数间距(IQR),它是上四分位数QU和下四分位数QL之差,其间包含全部观察值的一般,其值越大,说明数据的变异程度越大,离中趋势越明显。
5,对属性值进行基本的统计分析
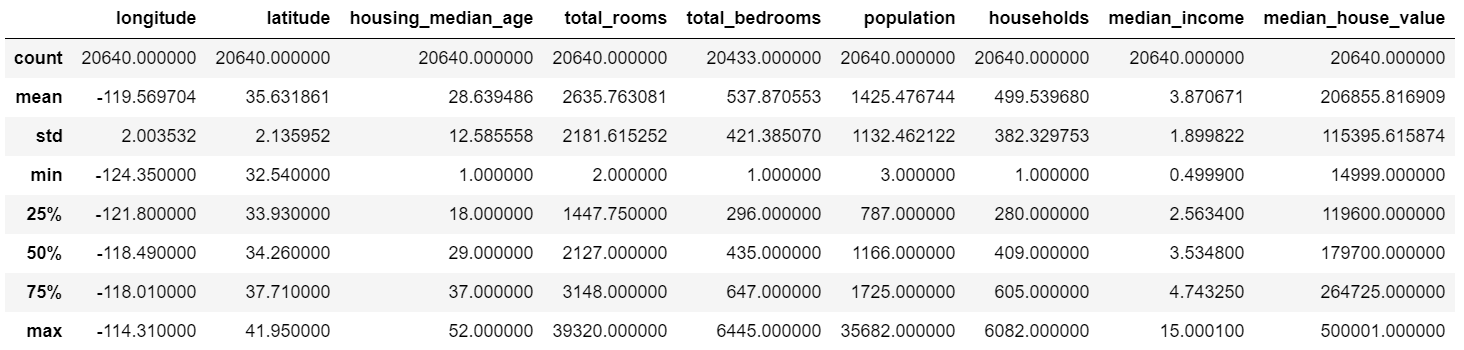
使用DataFrame的describe()函数,对变量属性进行基本的统计描述分析,行索引是count :表示统计非NaN的行数,mean表示均值,std表示标准差,最大值、最小值、上四分位数(25%),中位数(50%)和下四分位数(75%)。
housing.describe()
三,属性的直方图
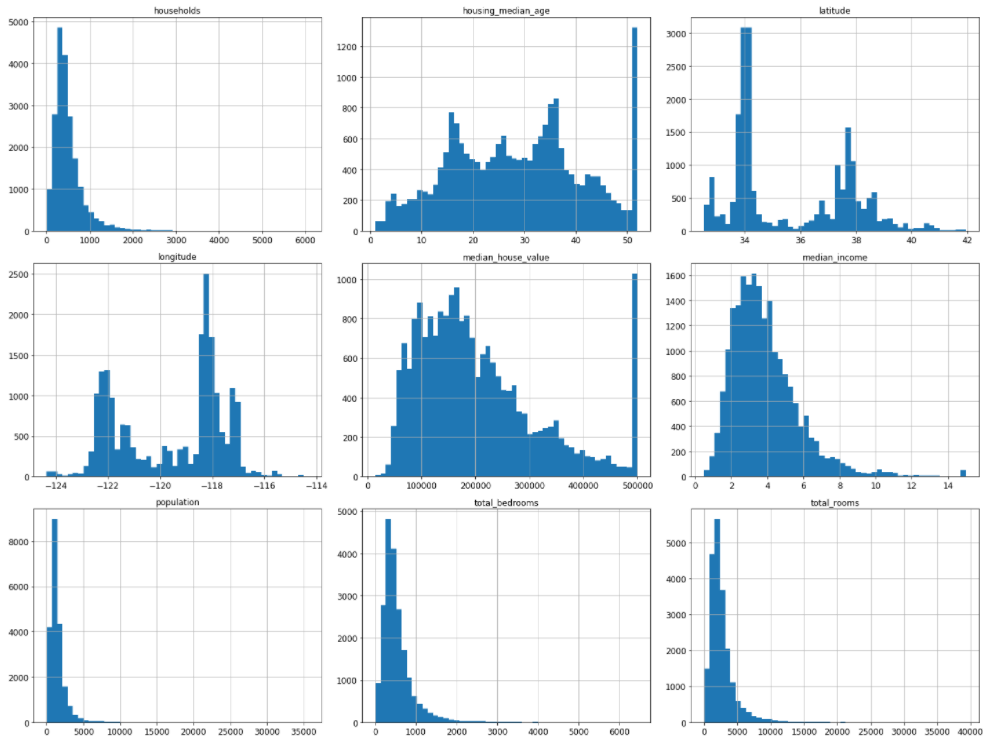
在Jupyter notebooks中显示属性的直方图,查看属性值的分布情况,通过DataFrame的hist(),可以对标量属性查看直方图。
%matplotlib inline import matplotlib.pyplot as plt housing.hist(bins=50, figsize=(20,15)) plt.show()
从直方图中可以看出,除了经纬度latitude 和 longitude之外,有5个属性households、population、total_bedrooms、total_rooms和meidan_income的直方图中出现重尾现象,呈现出左偏分布,中位数右侧的延伸比左侧要远的多,余下的2个属性 housing_median_age 和 median_house_value的直方图,最右侧都呈现出一个异常的值。
对于属性直方图中出现的重尾分布,有时需要对数据进行转换,比如计算其对数。
四,属性之间的相关性
利用相关系数查看各个属性之间的相关性,用于发现不同变量之间的关联性,关联是指数据之间变化的相似性,这可以通过相关系数来描述。发现相关性可以帮助你预测未来,而发现因果关系意味着你可以改变世界。
由于housing的数据集不大,可以使用DataFrame.corr()方法计算出每队属性之间的标准相关系数(也称作皮尔逊r),查看median_house_value和其他属性的相关系数:
corr_matrix = housing.corr() corr_matrix["median_house_value"].sort_values(ascending=False)
从相关系数中可以看出:median_house_value 和 median_income的相关系数是最高的,这也符合“房价和收入呈现正相”的常识。
median_house_value 1.000000
median_income 0.687160
total_rooms 0.135097
housing_median_age 0.114110
households 0.064506
total_bedrooms 0.047689
population -0.026920
longitude -0.047432
latitude -0.142724
Name: median_house_value, dtype: float64
还有一种方法用于检测属性之间的相关性,就是使用pandas的scatter_matrix函数,它会绘制出每个数值属性相对于其他数值属性的相关性。
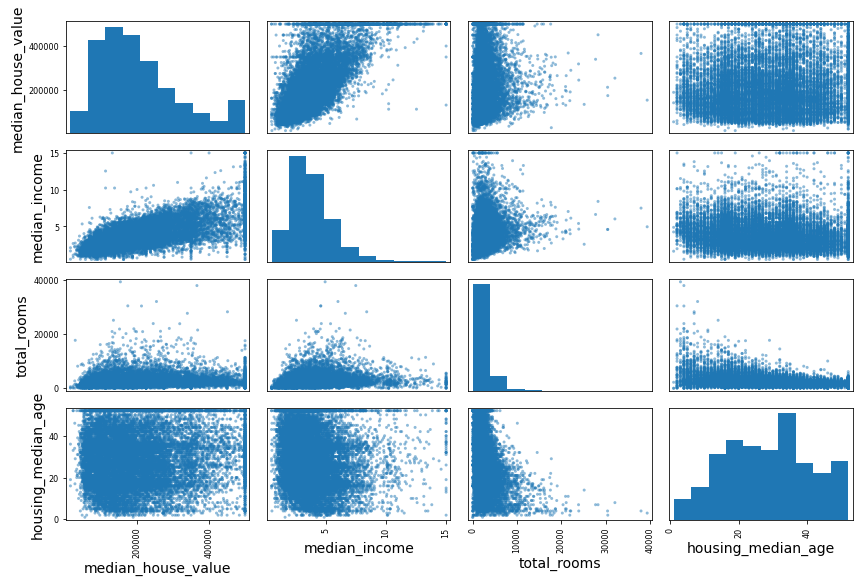
from pandas.plotting import scatter_matrix attributes = ["median_house_value", "median_income", "total_rooms", "housing_median_age"] scatter_matrix(housing[attributes], figsize=(12, 8))
由于篇幅无法完全展示9个属性的散点图矩阵,下面的散点图矩阵仅仅绘制出四个属性的相关性,主对角线位置(从左上到右下)是每个属性的直方图,其他网格是都是两个属性之间的相关性。
五,属性的组合
对变量属性进行组合,通常是跟标量属性推导出比率属性,比如,根据房间总数(total_rooms)和家庭总数(household)计算每个家庭的房间的数量,或者根据房间总数计算卧室的占比,或者根据人口和家庭来计算每个家庭的人口数量:
housing["rooms_per_household"] = housing["total_rooms"]/housing["households"] housing["bedrooms_per_room"] = housing["total_bedrooms"]/housing["total_rooms"] housing["population_per_household"]=housing["population"]/housing["households"] corr_matrix = housing.corr() corr_matrix["median_house_value"].sort_values(ascending=False)
计算新加的属性跟median_house_value的相关性:
median_house_value 1.000000
median_income 0.687160
rooms_per_household 0.146285
total_rooms 0.135097
housing_median_age 0.114110
households 0.064506
total_bedrooms 0.047689
population_per_household -0.021985
population -0.026920
longitude -0.047432
latitude -0.142724
bedrooms_per_room -0.259984
Name: median_house_value, dtype: float64
参考文档:
