本系列文章翻译自NIST(美国国家标准与技术研究院)的《Engineering Statistic Handbook》(工程统计手册) 的第6章第4节关于时间序列分析的内容。本文的翻译会先使用翻译软件进行初步翻译,笔者在对不恰当之处进行修正。由于笔者水平有限,翻译过程难免有疏漏之处,欢迎大家评论区指出。本站所有文章均为原创,转载请注明出处。
英文版地址:https://www.itl.nist.gov/div898/handbook/pmc/section4/pmc4.htm
6.4 时间序列分析
时间序列数据在监视工业流程或跟踪公司业务指标时经常出现。通过时间序列方法建模数据与使用本章前面讨论的过程监控方法之间的本质区别如下:
时间序列分析解释了这样一个事实:随着时间的推移,数据点可能有一个应该考虑的内部结构(如自相关、趋势或季节变化)。
本节将简要概述在时间序列建模和分析领域的丰富和快速增长的一些更广泛使用的技术。
1 定义、应用和技术
时间序列的定义: 一个变量的值在等时间间隔内的有序序列。
应用:时间序列模型的使用是双重的:
- 获得对产生观测数据的潜在结构的理解;
- 拟合一个模型,并继续预测,监测,甚至反馈和前馈控制。
时间序列分析用于许多应用,例如:
- 经济预测
- 销售预测
- 预算分析
- 股票市场分析
- 产量预测
- 过程和质量控制
- 库存研究
- 工作负载的预测
- 效用研究
- 统计分析
还有许许多多……
技术: 拟合时间序列模型可能是一项很有挑战的事情。模型拟合的方法有很多,包括以下几种:
- Box-Jenkins ARIMA模型
- Box-Jenkins多变量模型
- Holt-Winters指数平滑(单、双、三)
用户的应用和偏好将决定适当技术的选择。所有这些方法都超出了本手册作者的范围和意图。这里的概述将从一些基本的平滑技术开始:
- 平均方法
- 指数平滑技术。
本节稍后我们将讨论Box-Jenkins建模方法和多元时间序列。
2 什么是移动平均或平滑技术
随着时间的推移,收集的数据中会存在某种形式的随机变化。由于随机变化的影响,有一些减小和消除的方法。工业上常用的一种技术是“平滑”。如果应用得当,这种技术可以更清楚地揭示潜在的趋势、季节和循环成分。 有两组不同的平滑方法:
- 平均方法
- 指数平滑方法
我们将首先研究一些平均法,如“简单地” 平均所有过去数据。
仓库经理想知道一个典型的供应商以1000美元的单位交付多少货物。他随机抽取了12家供应商的样本,得到了以下结果:
| Supplier | $ | Supplier | $ |
|---|---|---|---|
| 1 | 9 | 7 | 11 |
| 2 | 8 | 8 | 7 |
| 3 | 9 | 9 | 13 |
| 4 | 12 | 10 | 9 |
| 5 | 9 | 11 | 11 |
| 6 | 12 | 12 | 10 |
数据的计算平均值= 10。经理决定使用它作为一个典型供应商的支出估算。 这是一个好估计还是坏估计?
我们将计算“均方误差”:
- “误差”=实际花费的金额减去估计的金额。
- “误差平方”就是上面的误差在取平方。
- “SSE”是误差平方的和。 (sum squared error)
- MSE是误差平方的均值。(mean squared error)
结果是: 误差和平方误差 估算值= 10
| Supplier | $ | Error | Error Squared |
|---|---|---|---|
| 1 | 9 | -1 | 1 |
| 2 | 8 | -2 | 4 |
| 3 | 9 | -1 | 1 |
| 4 | 12 | 2 | 4 |
| 5 | 9 | -1 | 1 |
| 6 | 12 | 2 | 4 |
| 7 | 11 | 1 | 1 |
| 8 | 7 | -3 | 9 |
| 9 | 13 | 3 | 9 |
| 10 | 9 | -1 | 1 |
| 11 | 11 | 1 | 1 |
| 12 | 10 | 0 | 0 |
SSE = 36,MSE = 36/12 = 3.
那么,对于每个供应商所花费的金额,估计器是否最优呢? 让我们比较一下这个估计(10)和下面的估计:7、9和12。也就是说,我们估计每个供应商将花费7美元、9美元或12美元。
执行相同的计算,我们得到:
| Estimator | 7 | 9 | 10 | 12 |
|---|---|---|---|---|
| SSE | 144 | 48 | 36 | 84 |
| MSE | 12 | 4 | 3 | 7 |
均方误差最小的估计量为最佳估计量。可以从数学上证明,使一组随机数据的均方差最小的估计量是均值。
接下来,我们将检验均值,看看它在预测净利润方面的表现。 下一个表格给出了个人电脑制造商在1985年到1994年之间的税前收入。
| Year | $ (millions) | Mean | Error | Squared Error |
|---|---|---|---|---|
| 1985 | 46.163 | 48.676 | -2.513 | 6.313 |
| 1986 | 46.998 | 48.676 | -1.678 | 2.814 |
| 1987 | 47.816 | 48.676 | -0.860 | 0.739 |
| 1988 | 48.311 | 48.676 | -0.365 | 0.133 |
| 1989 | 48.758 | 48.676 | 0.082 | 0.007 |
| 1990 | 49.164 | 48.676 | 0.488 | 0.239 |
| 1991 | 49.548 | 48.676 | 0.872 | 0.761 |
| 1992 | 48.915 | 48.676 | 0.239 | 0.057 |
| 1993 | 50.315 | 48.676 | 1.639 | 2.688 |
| 1994 | 50.768 | 48.676 | 2.092 | 4.378 |
MSE = 1.8129.
问题来了:如果我们怀疑一种趋势,我们能使用平均值来预测收入吗?下面的图表清楚地表明,我们不应该这样做。
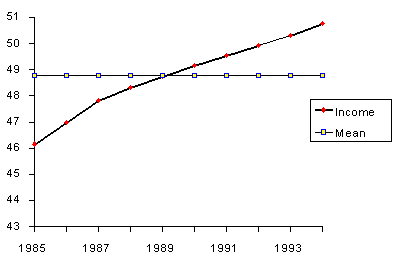
总之,我们指出:
-
过去所有观测的“简单”平均数或平均值,只有在没有趋势的情况下,才对预测有用。如果有趋势,需要使用不同的估计考虑到趋势。
-
过去所有观测结果的平均“权重”都是相等的。例如,3、4、5的平均值是4。当然,我们知道,平均值是通过将所有数值相加,然后除以数值的个数来计算的。另一种计算平均值的方法是将每个数值乘数值的个数的倒数在相加,如:
3/3 + 4/3 + 5/3 = 1 + 1.3333 + 1.6667 = 4。
乘数1/3称为权重。一般来说:
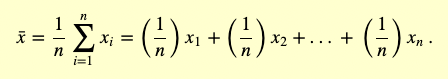
(1/n)是权重,当然,它们加起来等于1。
2.1 单次移动平均(Single Moving Average)
总结过去数据的另一种方法是按如下方法计算连续较小的过去数据集的平均值。
回想一下这组数字 9, 8, 9, 12, 9, 12, 11, 7, 13, 9, 11, 10 是随机选择的12个供应商的金额。设“小集合”的大小M为3。那么前3个数字的平均值是:(9 + 8 + 9)/ 3 = 8.667。
这被称为“平滑”(即某种形式的平均)。这个平滑过程继续前进一个周期,计算三个数字的下一个平均值,去掉第一个数字。
下表总结了这个过程,它被称为移动平均。移动平均的一般表达式是:
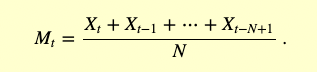
移动平均结果
| Supplier | $ | MA | Error | Error squared |
|---|---|---|---|---|
| 1 | 9 | |||
| 2 | 8 | |||
| 3 | 9 | 8.667 | 0.333 | 0.111 |
| 4 | 12 | 9.667 | 2.333 | 5.444 |
| 5 | 9 | 10.000 | -1.000 | 1.000 |
| 6 | 12 | 11.000 | 1.000 | 1.000 |
| 7 | 11 | 10.667 | 0.333 | 0.111 |
| 8 | 7 | 10.000 | -3.000 | 9.000 |
| 9 | 13 | 10.333 | 2.667 | 7.111 |
| 10 | 9 | 9.667 | -0.667 | 0.444 |
| 11 | 11 | 11.000 | 0 | 0 |
| 12 | 10 | 10.000 | 0 | 0 |
MSE = 2.42,而前面情况的MSE为3。
2.2 中心移动平均(Centered Moving Average)
在之前的例子中,我们计算了前3个时间周期的平均值,并将其放在周期3旁边。我们可以把平均值放在三个时段的中间,也就是,在时段2旁边。对于奇数时间段,这种方法很有效,但对于偶数时间段就不那么有效了。当M = 4时,我们应该把第一个移动平均值放在哪里?
从技术上讲,移动平均值将在t = 2.5, 3.5,… 为了避免这个问题,我们使用M = 2平滑MA。因此我们需要平滑已经平滑过的值!
下表显示了M = 4时的结果。中间步骤:
| Period | Value | MA | Centered |
|---|---|---|---|
| 1 | 9 | ||
| 1.5 | |||
| 2 | 8 | ||
| 2.5 | 9.5 | ||
| 3 | 9 | 9.5 | |
| 3.5 | 9.5 | ||
| 4 | 12 | 10.0 | |
| 4.5 | 10.5 | ||
| 5 | 9 | 10.750 | |
| 5.5 | 11.0 | ||
| 6 | 12 | ||
| 6.5 | |||
| 7 | 11 |
这是最终的表格:
| Period | Value | Centered MA |
|---|---|---|
| 1 | 9 | |
| 2 | 8 | |
| 3 | 9 | 9.5 |
| 4 | 12 | 10.0 |
| 5 | 9 | 10.75 |
| 6 | 12 | |
| 7 | 11 |
线性趋势过程中的双移动平均(Double Moving Averages for a Linear Trend Process)
不幸的是,无论是所有数据的平均值,还是最近M个值的移动平均,当用作下一时期的预测时,都不能处理具有显著趋势的数据。
存在一个变化的MA程序,可以更好地处理具有趋势的数据。它被称为线性趋势过程的双移动平均。它从原始移动平均计算第二个移动平均,使用相同的M值。只要单和双移动平均是可用的,计算机程序使用这些平均来计算斜率和截距,然后进行预测。