【字符串算法3】浅谈KMP算法

【字符串算法1】 字符串Hash（优雅的暴力）

【字符串算法2】Manacher算法

【字符串算法3】KMP算法

这里将讲述  【字符串算法3】KMP算法

Part1 理解KMP的精髓和思想

其实KMP我也不太懂。。有可能会误人子弟qwq

好的吧现在开始

KMP处理这样一个问题：

给出两个字符串s1和s2，其中s2为s1的子串，求出s2在s1中所有出现的位置。

一般的博客都是讲述怎么怎么暴力匹配，然后再讲KMP算法，显然这样的安排是不合适的，

因为来看KMP的OIer基本上都是会暴力匹配的。

那么我们节约时间直接从KMP算法开始，如果不会暴力匹配，右转字符串入门练习场

概念：

模式串：记为T，表示待匹配的串即T在某个长串中的位置即为所求

文本串：记为S，表示待匹配的文本

一般情况下|T|<=|S|，显然当|T|>|S|时输出为空

失配：对于S[j]！=T[i] 我们称两个串在二元组（i，j）时失配

首先是KMP的精髓：

对于每次失配之后，我都不会从头重新开始枚举，

而是根据我已经得知的数据，从某个特定的位置开始匹配；

而对于模式串的每一位，都有唯一的“特定变化位置”，这个在失配之后的特定变化位置可以帮助我们利用已有的数据不用从头匹配，

从而节约时间。

第一步我们需要知道上述两个关键词，找出对于模式串每一个位子失配然后移到的那个位置。（即next数组）

其实，next数组的理解才是KMP中的难点，一般来说我们定义next数组为： 

next[]表示 ： 模式串每i位子失配时然后移到的那个位置（这里是指向模式串的指针i指向的位置，而不是真实的将模式串移动）

显然，上述定义是完全正确的。 但是等于什么都没说。

【我也知道啊，关键是怎么求】

我现在给出我对next数组的理解

在模式串中，对于每一位 T（i）它的 next 数组应当是记录一个位置 j, | j≤i 并且满足 T[i]==T[j] 并且在 j不等于1 时

 理应满足T[1]至T[j-1]分别与 T[i−j+1]~T[i−1] 按位相等

那么next数组中存在的是一个元素j要求保证1到j前面那个字符，和i前面j-1个字符完全相等

（注意到此时若i失配我们就可以把指针跳到next[i]就不会有冗余比较了）

举个栗子：

模式串：a b c a b
文本串：a b c a c a b a b c a b 

求出模式串的next数组（当且仅当不存在符合条件的j的时候是0）

next： 0 0 0 1 2
模式串：a b c a b
文本串：a b c a c a b a b c a b

当发现b和c不相等的时候吧指针移到next[5]=2即从第二位重新比较（根据上述next的定义我们知道第1-1和第4-4是一样的串）

next：       0 0 0 1 2
模式串：      a b c a b
文本串：a b c a c a b a b c a b

当发现b和c不相等的时候又从头开始比较

next：         0 0 0 1 2
模式串：        a b c a b
文本串：a b c a c a b a b c a b

一直暴力向后找 直到：

next：               0 0 0 1 2
模式串：              a b c a b
文本串：a b c a c a b a b c a b

找到一个匹配，那么好记录下来这个时候的位置 8 又发现指针指向头跳出

再来一个：

next： 0 0 0 1 2 3
模式串：a b c a b c
文本串：a b c a b d a b a b c a b c

当第6位失配的时候直接往后移动next[6]=3位（实现的时候就是指向模式串的指针 i 赋值为next[i]就行）

next：       0 0 0 1 2 3 
模式串：      a b c a b c
文本串：a b c a b d a b a b c a b c

看到这里你好像理解了KMP的实质，现在再来强调一下：

对于每次失配之后，我都不会从头重新开始枚举，

而是根据我已经得知的数据，从某个特定的位置开始匹配；

而对于模式串的每一位，都有唯一的“特定变化位置”，这个在失配之后的特定变化位置可以帮助我们利用已有的数据不用从头匹配，

从而节约时间。

Part2 KMP算法next数组的构造和代码实现

啊啊啊啊啊，经过冗长的KMP的介绍现在终于搞清楚KMP算法，

其实质上面强调过了，要确保KMP的思想已经看懂了然后来写代码

next数组怎么构造是一个玄学问题，（构造就是求的意思）

一句话解决：用模式串自己匹配自己就行

void getnext()
{
    int i=0,j=-1;next[0]=-1;  //-1表示没有
    while (i<lenT) {
        if (j==-1||T[i]==T[j]) {  //没有或者是匹配
            i++,j++; //往后移
            next[i]=j; //赋值表示1到j和i-j+1到i-1都匹配
        }else j=next[j]; //跳
    }
}

实在不行就背模板吧。

Part3 KMP算法匹配代码实现

void kmp()
{
    int i=0,j=0; //i指针指向文本串，j指针指向模式串
    while (i<lenS&&j<lenT) {
        if (j==-1||S[i]==T[j]){ //前面没的好跳（j==-1然后++j以后j就为0了又从头）或者这位匹配往后跳1位
            i++,j++;
        } else j=next[j]; //往前跳找一个前面匹配无误的位置再暴力匹配
        if (j==lenT) j=next[j],printf("%d
",i-lenT+1); //找到啦，输出位置
    }
}

Part4 KMP算法模板题目和程序设计

 P3375 【模板】KMP字符串匹配

题目描述

如题，给出两个字符串s1和s2，其中s2为s1的子串，求出s2在s1中所有出现的位置。

为了减少骗分的情况，接下来还要输出子串的前缀数组next。

（如果你不知道这是什么意思也不要问，去百度搜[kmp算法]学习一下就知道了。）

输入输出格式

输入格式：

第一行为一个字符串，即为s1

第二行为一个字符串，即为s2

输出格式：

若干行，每行包含一个整数，表示s2在s1中出现的位置

接下来1行，包括length(s2)个整数，表示前缀数组next[i]的值。

输入输出样例

输入样例#1： 

ABABABC
ABA

输出样例#1： 

1
3
0 0 1 

说明

时空限制：1000ms,128M

数据规模：

设s1长度为N，s2长度为M

对于30%的数据：N<=15，M<=5

对于70%的数据：N<=10000，M<=100

对于100%的数据：N<=1000000，M<=1000000

样例说明：

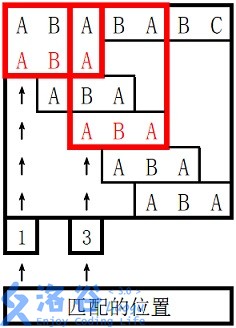
所以两个匹配位置为1和3，输出1、3

代码实现：

# include <bits/stdc++.h>
using namespace std;
const int MSXN=1000005;
char S[MSXN],T[MSXN];
int next[MSXN],lenT,lenS;
void getnext()
{
    int i=0,j=-1;next[0]=-1;
    while (i<lenT) {
        if (j==-1||T[i]==T[j]) {
            i++,j++;
            next[i]=j;
        }else j=next[j];
    }
}
void kmp()
{
    int i=0,j=0;
    while (i<lenS&&j<lenT) {
        if (j==-1||S[i]==T[j]){
            i++,j++;
        } else j=next[j];
        if (j==lenT) j=next[j],printf("%d
",i-lenT+1);
    }
}
int main()
{
    scanf("%s",S);lenS=strlen(S);
    scanf("%s",T);lenT=strlen(T);
    getnext();
    kmp();
    for (int i=1;i<=lenT;i++) printf("%d ",next[i]);
    return 0;
}