(这里是Splay基础操作,reserve什么的会在下一篇里面讲)
好久之前就说要学Splay了,结果苟到现在才学习。
可能是最近良心发现自己实在太弱了,听数学又听不懂只好多学点不要脑子的数据结构。
感觉Splay比Treap良心多了——代码真的好写。
对于Splay显然可以维护Treap的所有操作,并且本质是BST。
先看看Splay是怎么维护普通平衡树操作的吧。
首先先定义一些基础的变量(若不作特殊说明这些变量的意义不变)
int t[N][2] // t[x][0]表示节点x的左子树,t[x][1]表示节点x的右子树
int cnt[N] // cnt[x]表示节点x存储多少个重复的数
int val[N] // val[x]表示节点x存储数的大小
int par[N] // par[x]表示节点x的直接父亲,特别的,根节点的直接父亲为0
int size[N] // size[x]表示在BST中x子树中存储数的个数
Check(x) 函数 :
询问节点x是其父亲的左儿子(return 0)还是右孩子(return 1)
int check (int x) { return rs(par[x])==x; }
由上述代码可知,根节点的check(root)值为0,即根节点是0节点的左儿子(Nothing Special)
Up(x)函数:
对于节点x维护其size值为两个孩子的size值+自身cnt值。
void up(int x){ size[x]=size[ls(x)]+size[rs(x)]+cnt[x]; }
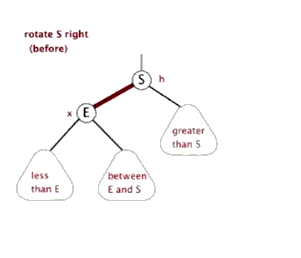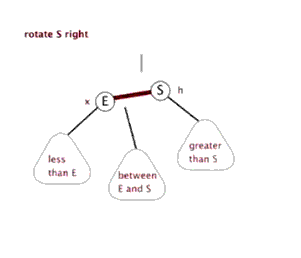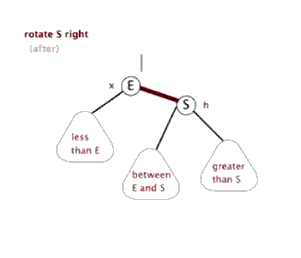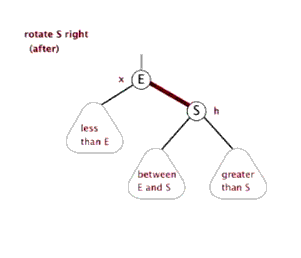
Rotate(x)函数:
对于节点x旋转到其父亲节点,且不改变树BST性质。(使得树形态较为随机)
这里需要解释一下Rotate的解释和记忆方法(和Treap中Rotate类似)
对于一棵有根树(且父亲指向儿子的边有向),我们现在以把左儿子旋到父节点为例。
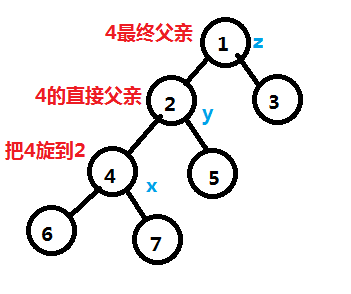
第1步,考虑4的右子树已经有元素了,考虑把右子树连接到父节点左儿子处。不改变BST性质。
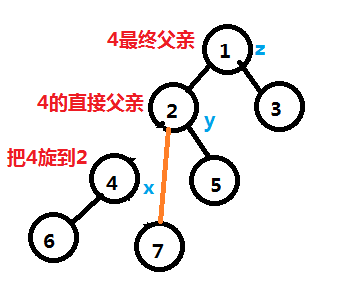
在此基础上考虑第二步,就是吧2(4的直接父亲接到4的右边)不改变BST性质。
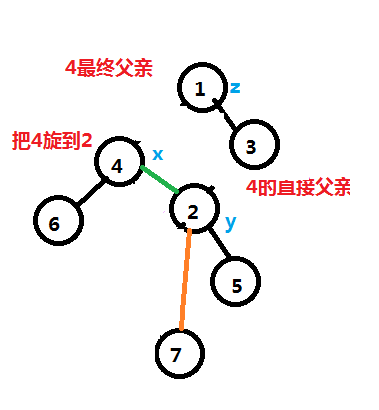
这个时候我们会发现,只进行第三部就可以完成一次rotate操作。
即连一条1指向4的边即可。
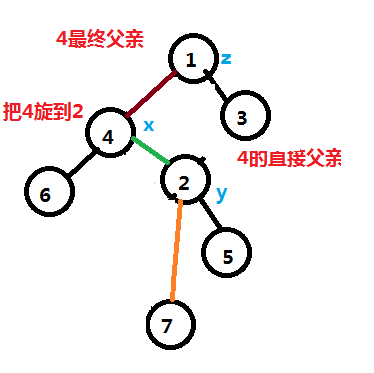
对于左边节点转到父亲节点,一般称之为右旋
对于右旋函数的代码,不难得到。

void rotate(int x){ int y=par[x]; t[y][0]=t[x][1]; par[t[x][1]]=y; t[x][1]=y; t[par[y]][check(y)]=x; par[x]=par[y]; par[y]=x; up(y); up(x); }
那左旋呢???
所有0和1的地方去个反不就好了!!!(至少我是那么记的)
对于 真正的旋转代码:
void rotate(int x){ int y=par[x],k=check(x); t[y][k]=t[x][k^1]; par[t[x][k^1]]=y; t[x][k^1]=y; t[par[y]][check(y)]=x; par[x]=par[y]; par[y]=x; up(y); up(x); }
Splay(x,goal) 操作
把节点x通过若干次rotate操作使其到达目标节点goal或者为根,而goal却成为节点x的儿子。
我们可以分三种情况讨论:
1. goal 是 x的直接父亲(边界),那么直接将x旋到父亲位置即可
2. x和x的直接父亲y和x的爷爷z在同一条直线上(不会打结吗?我们需要给定一种顺序)
那么先旋转父亲y,再旋转x,这个时候想就被旋转到y和z节点上方了。
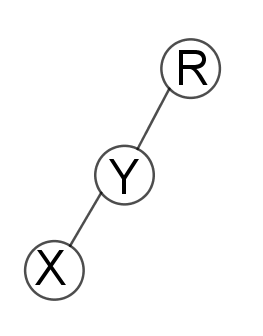
3. x和x的直接父亲y和x的爷爷z在不在同一条直线上(直接把x转两次不就行了么)
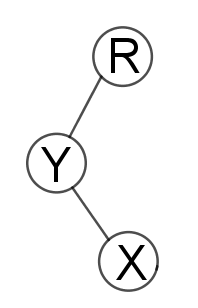
我们可以参考下图,模拟一条链上的Splay操作。

简单的代码实现如下(自然语言是多么的无力....)
void splay(int x,int goal=0) { while (par[x]!=goal) { int y=par[x],z=par[y]; if (z!=goal) { if (check(x)==check(y)) rotate(y); else rotate(x); } rotate(x); } if (!goal) root=x;
}
Insert(x)操作
插入一个值为x的元素。
显然从根节点开始按照BST性质访问Splay,直到找到一个节点v,其值val[v]恰好为x,那么直接增加个数
如果找不到节点的的val[v]恰好为x,那么新建一个节点即可。
最后Splay一下防止出现长链的情况。
void insert(int x) { int cur=root,p=0; while (cur && val[cur]!=x) p=cur,cur=t[cur][x>val[cur]]; if (cur) cnt[cur]++; else { cur=++tot; if (p) t[p][x>val[p]]=cur; ls(cur)=rs(cur)=0; par[cur]=p; val[cur]=x; size[cur]=cnt[cur]=1; } splay(cur); }
Find(x)函数
将val值小于等于x的val值最大一个节点,旋转到根。
题目解决在于如何找到val值小于等于x的val最大的一个节点,注意不能找到空节点,所以要判断。
找到节点v直接利用Splay操作,旋转到根即可。
void find(int x){ if (!root) return; int cur=root; while (t[cur][x>val[cur]] && val[cur]!=x) cur=t[cur][x>val[cur]]; splay(cur); }
Rank(x)函数
求值x的排名(x可能曾经没有出现过),排名的定义是比x小的元素个数+1。
利用find操作后,如果x之前出现过,即val[root]=x,那么直接输出左子树的size
否则那么根节点一定比x小那么还需要加上根节点的cnt
int rank(int x){ find(x); if (val[root]>=x) return size[ls(root)]; else return size[ls(root)]+cnt[root]-1; }
pre(x)和suc(x)函数
求值x的前驱(比x小的最大数,若没有是-无穷),求值x的后继(比x大的最小数,若没有是+无穷),x可能没有出现过。
求前驱,考虑find操作以后小于等于x的元素都在根及根的左侧,那么如果根直接小于x(x之前没出现过),那么直接打印根就行
否则在左子树中找一直往右子树走找最大的即可。
求后继,考虑find操作以后大于等于x的元素都在根及根的左侧,那么如果根直接大于x(x之前没出现过),那么直接打印根就行
否则在右子树中找一直往左子树走找最小的即可。
int pre_id(int x) { find(x); if (val[root]<x) return root; int cur=ls(root); while (rs(cur)) cur=rs(cur); return cur; } int pre_val(int x){ return val[pre_id(x)]; } int suc_id(int x) { find(x); if (val[root]>x) return root; int cur=rs(root); while (ls(cur)) cur=ls(cur); return cur; } int suc_val(int x){ return val[suc_id(x)]; }
erase(x)操作
删除权值为x的一个数。
考虑数x的前驱和后继是唯一的,那么求出x的前驱和x的后继,均用Splay操作转到根节点和根节点的右儿子处,
那么根节点右儿子的左儿子一定就可知道是x的了。直接删除它即可,特别的是,剩余个数大于1和等于1的时候需要不同处理
其中大于1的时候,直接吧cnt减去1即可,等于1的时候,则需要删除节点所有的信息。
void erase(int x){ int last=pre_id(x),next=suc_id(x); splay(last),splay(next,last); int d=ls(rs(root)); if (cnt[d]>1) cnt[d]--,splay(d); else t[next][0]=0; }
Treap模板题目:https://www.luogu.org/problemnew/show/P3369

# include <bits/stdc++.h> using namespace std; const int N=2e5+10; struct Splay{ # define ls(x) (t[x][0]) # define rs(x) (t[x][1]) # define inf (0x3f3f3f3f) int t[N][2],cnt[N],val[N],size[N],par[N]; int root,tot; Splay() { tot=root=0; insert(-inf); insert(inf);} int check(int x) { return rs(par[x])==x; } void up(int x){ size[x]=size[ls(x)]+size[rs(x)]+cnt[x]; } void rotate(int x){ int y=par[x],k=check(x); t[y][k]=t[x][k^1]; par[t[x][k^1]]=y; t[x][k^1]=y; t[par[y]][check(y)]=x; par[x]=par[y]; par[y]=x; up(y); up(x); } void splay(int x,int goal=0) { while (par[x]!=goal) { int y=par[x],z=par[y]; if (z!=goal) { if (check(x)==check(y)) rotate(y); else rotate(x); } rotate(x); } if (!goal) root=x; } void insert(int x) { int cur=root,p=0; while (cur && val[cur]!=x) p=cur,cur=t[cur][x>val[cur]]; if (cur) cnt[cur]++; else { cur=++tot; if (p) t[p][x>val[p]]=cur; ls(cur)=rs(cur)=0; par[cur]=p; val[cur]=x; size[cur]=cnt[cur]=1; } splay(cur); } void find(int x){ if (!root) return; int cur=root; while (t[cur][x>val[cur]] && val[cur]!=x) cur=t[cur][x>val[cur]]; splay(cur); } int pre_id(int x) { find(x); if (val[root]<x) return root; int cur=ls(root); while (rs(cur)) cur=rs(cur); return cur; } int pre_val(int x){ return val[pre_id(x)]; } int suc_id(int x) { find(x); if (val[root]>x) return root; int cur=rs(root); while (ls(cur)) cur=ls(cur); return cur; } int suc_val(int x){ return val[suc_id(x)]; } int rank(int x){ find(x); if (val[root]>=x) return size[ls(root)]; else return size[ls(root)]+cnt[root]-1; } int kth_id(int k) { if (k>tot||k<0) return -1; int cur=root; while (true) { if (t[cur][0]&&k<=size[ls(cur)]) cur=ls(cur); else if (k>size[ls(cur)]+cnt[cur]) { k-=size[ls(cur)]+cnt[cur]; cur=rs(cur); } else return cur; } } int kth_val(int k){ return val[kth_id(k+1)]; } void erase(int x){ int last=pre_id(x); int next=suc_id(x); splay(last); splay(next,last); int d=ls(rs(root)); if (cnt[d]>1) cnt[d]--,splay(d); else t[next][0]=0; } }tr; int main() { int T; scanf("%d",&T); while (T--) { int op,x; scanf("%d%d",&op,&x); switch(op) { case 1:tr.insert(x);break; case 2:tr.erase(x);break; case 3:printf("%d ",tr.rank(x));break; case 4:printf("%d ",tr.kth_val(x));break; case 5:printf("%d ",tr.pre_val(x));break; case 6:printf("%d ",tr.suc_val(x));break; } } return 0; }