回归的分类器
- 是一种名为"回归"的线性分类器, 其本质是由线性回归变化而来的.
- Z = θ0 + θ1x1 + θ2x2 +...+ θnxn
- 其中: θ被统称为模型的参数, θ0 被称为截距, θ1 ~ θn 被称为系数, 我们可以将系数和自变量用矩阵来表示

- 线性回归的任务, 就是构造一个预测函数z来映射输入的特征矩阵x和标签值y的线性关系, 而构造预测函数的核心就是找出模型的参数: θT和θ0
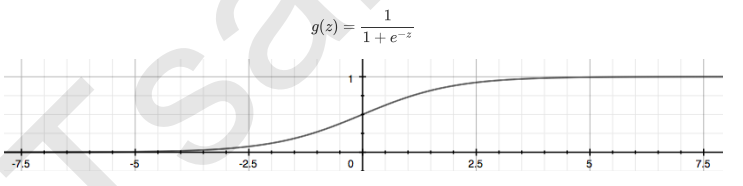
- 当标签是离散型变量, 尤其是满足0-1分布的离散型变量, 我们引入联系函数(link function), 将线性回归方程Z变换为g(z), 并且令g(z)的值分布在(0,1)之间, 且当g(z)接近0时,样本的标签类别为0, 当g(z)接近1时样本的标签类别为1, 这样就得到一个分类模型, 对于逻辑回归来说就是sigmod函数
-
我们实际上是在对线性回归弄醒的预测结果取对数几率来让其的结果无限逼近0和1, 因此, 其对应的模型被称为"对数几率回归", 也就是说我们的逻辑回归, 这个名为"回归"确实用来做分类工作的分类器
- 逻辑回归返回的数字, 即便本质上不是概率, 却也有概率的本质, 可以被当成时概率来看待和使用
逻辑回归的优点:
- 逻辑回归对线性关系的拟合效果非常好, 特征与标签之间线性关系极强的数据, 比如金融领域的信用卡欺诈, 评分卡制作, 电商中的营销预测等等相关的数据, 都是逻辑回归的强项, 虽然现在由了梯度提升树GDBT, 比逻辑回归效果更好, 也被许多数据咨询公司启用, 但逻辑回归在金融领域, 尤其使银行业中的统治地位依然不可动摇
- 逻辑回归计算快: 对于线性数据, 逻辑回归的拟合和计算都非常快, 计算效率优于SVM和随机森林.
- 逻辑回归返回的分类结果不是固定的0,1, 而是以小数形式呈现的类概念数字: 王i们因此可以把逻辑回归返回的结果当成连续型舒俱来用, 比如在评分卡的制作上, 我们不仅需要判断客户是否违约, 还需要给出确定的"信用分", 而这个信用分的计算就需要使用分类概率计算出对数几率, 而决策树和随机森林这样的分类器, 可以产出分类结果, 却无法帮我们计算分数
- 逻辑回归还有抗噪能力强的优点, 当AUC面积好于0.8的时候,逻辑回归优于树模型
逻辑回归的本质:
- 她是一个返回对数几率,在线性数据上表现优异的分类器, 它主要应用在金融领域, 其数学目的时求解能够让模型对数据拟合程度很高的参数θ的值, 以此构建预测函数y(x), 然后将特征矩阵输入预测吃函数来计算逻辑回归的结果y
二元逻辑回归的算是函数
- 逻辑回归有这基于训练数据求参数θ的需求, 并且希望训练出来的模型能够尽可能地拟合训练数据, 即模型在训练集上的预测准确率越靠近100%越好
- 因此我们使用损失函数这个评估指标, 来衡量参数为θ的模型拟合训练时产生的信息损失的大小, 并依次衡量参数θ的优劣
损失函数:
- 衡量参数θ的优劣的指标, 用来求解最优参数的工具
- 损失函数小, 模型在训练集上表现优异, 拟合充分, 参数优秀
- 损失函数大, 模型在训练集上表现差劲 拟合不足, 参数糟糕
- 注意: 没有"求解参数"需求的模型没有损失函数, 比如KNN, 决策树
逻辑回归的损失函数时由极大似然估计推导出来的, 具体的结果:
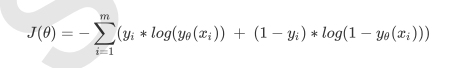
- 其中θ表示求解出来的一组参数, m时样本的个数, yi时样本i上的真实标签, yθ(xi)时样本i上, 基于参数θ计算出来的逻辑回归返回值, xi时样本i各个特征的取值.
- 由于我们追求损失函数的最小值, 让模型在训练集上表现最优, 可能你会引发另一个问题,: 如果模型在训练集上表现优秀, 却在测试集上表现糟糕, 模型就会过拟合, 虽然逻辑回归时天生欠拟合的模型, 但我们还是需要控制过拟合技术帮助我们调整模型, 对逻辑回归中过拟合的控制, 通过正则化来实现
似然和概率:
- 对于表达式而言, 如果参数θ时已知的, 特征向量xi是未知的, 我们便称p时再探索不同特征取值下获取所有可能性y'的可能性, 这种坑你性就被称为概率, 研究的是自变量和因变量之间的关系
- 如果特征向量xi是已知的, 参数θ是未知的, 我们便称p是再探索不同参数下获取所有可能的y'的可能性, 这种可能性就被称为似然, 研究的是参数取值与因变量之间的关系
正则化:
- 正则化是用来防止模型过拟合的过程, 常用的有L1, L2正则化, 分别通过损失函数后加上参数向量θ的L1范式, L2范式的倍数来实现, 这个增加的范式, 被称为"正则项", 也被称为"惩罚项", 损失函数改变, 基于损失函数的最优化来求解的参数取值必然改变, 我们以次来调节模型拟合程度,
- 其中L1范式表现为参数向量中的每个参数的绝对值之和,
- L2范式表现为参数向量中每个参数的平方和的开方值
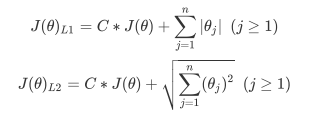
- 其中J(θ)是损失函数, C是用来控制正则化程度的超参数, n是方程中特征的总数, 也是方程中参数的总数, j代表每个参数, 再这里j要大于1, 是因为我们的参数向量θ中, 第一个参数是θ0, 是我们的截距, 它通常不参与正则化
- L1正则化和L2正则化虽然都可以控制过拟合, 但它们的效果并不相同, 当正则化强度逐渐增大(即C逐渐变小), 参数θ的取值会逐渐变小, 但L1正则化会将参数压缩为0, L2正则化只会让参数尽量小, 不会取到0
- 在L1正则化在逐渐加强的过程中, 携带信息量小的, 对模型贡献不大的张特征的参数, 会比携带大量信息, 对模型有巨大贡献的特征的参数更快的变为0, 所以L1正则化本质是一个特征选择的过程, 掌管了特征的稀疏性. L1正则化越强, 参数向量中旧越多的参数为0, 参数就越稀疏, 选出来的特征就越少, 以此来防止过拟合, 因此, 如果特征量很大, 数据维度很高, 我们会倾向于使用L1正则化这个性质, 逻辑回归的特征选择可以由嵌入法(Embedded)来完成
- L2在加强的过程中, 会尽量让每一个特征对模型都有一些小的贡献, 但携带信息少, 对模型贡献不大的特征的参数会非常接近0, 通常来说, 我焖主要的目的只是为了防止过拟合, 选择L2正则化就足够了, 但是如果选择L2正则化后还是过拟合, 模型在未知数据集上表现很差, 我们就可以考虑L1正则化
逻辑回归中的特征工程
- 我们通常使用L1的嵌入法来进行特征选择, 因为L1正则化的时候, 可以使特征携带信息量不那么大的特征丢弃掉, 进而完成特征选择
梯度下降:
- 在多元函数上对各个自变量求∂偏导数, 把求得的各个自变量的偏导数以向量的形式写出来, 就是梯度
- 求解梯度, 使在损失函数J(θ1, θ2)上对损失函数自身的自变量(θ1, θ2)求偏导数, 而这两个自变量,刚好使逻辑回归的预测函数y(x) = 1/[1+e(-θTx)]的参数
- max_iter: max_iter越大, 代表的步长越小, 反之, 则代表步长设置的很大, 模型迭代时间很短
样本不平衡与参数class_weight:
- 样本不平衡是指在一组数据中, 标签的一类天生占有很大的比例, 或误分类的代价很高, 即我们想要捕捉出某种特定的分类的时候的状况
- 当样本标签不均衡时, 此时耳朵class_weight对样本标签进行一定的均衡, 给少量的标签更多的权重, 让模型更偏向少数类,向捕获少数类的方向建模
- 我们有处理样本不均衡的各种方法, 其中主流的时采样法
- 上采样: 增加少数类的样本
- 下采样: 减少多数类的样本
描述性统计
- 日常处理异常值, 我们使用箱线图或者3σ法则来找到异常值
- 我们往往使用普通的描述性统计来观察数据的异常与数据的分布情况,, 注意, 这种方法只能在特征量有限的情况下进行, 如果有好几百个特征, 又无法降维或者特征选择不管用的情况下, 还是用3σ比较好
分箱
- 分箱时将连续型变量离散化, 所以箱子个数不能太多, 最好控制在10个以下, 离散化连续变量必然伴随这信息得损失, 并且箱子越少, 信息损失越大, 为了衡量特征上得信息以及特征对预测函数得贡献, 银行业定义了概念Information Value(IV)
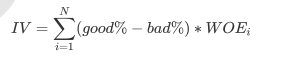
-
其中N时这个特征上箱子得个数, I代表每个箱子, good%时这个箱内得优质客户(标签为0得客户)占整个特征中所有优质客户得占比, bad%时这个箱子得坏客户(标签为1得哪些客户)占整个特征中所有坏客户得比例, WOE公式如下:
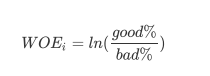
- 这是我们在银行业中用来衡量违约概率得指标, 中文叫做证据权重, 本质其实就是优质客户比上坏客户得比例得对数, WOE时对一个箱子来说得, WOE越大,代表这个箱子里得优质客户越多, 而IV是对整个特征来说得, IV代表得意义, 结合下表来说明
| IV | 特征对预测函数的贡献 |
| <0.3 | 特征几乎不带有有效信息, 对模型没有贡献, 这种特征可以被删除 |
| 0.03~0.09 | 有效信息很少, 对模型的贡献度低 |
| 0.1~0.29 | 有效信息一般, 对模型的贡献度中等 |
| 0.3~0.49 | 有效信息较多, 对模型的贡献度较高 |
| >=0.5 | 有效信息非常多, 对模型的贡献度超高并且可疑 |
-
-
- 可见,IV并非越大越好, 我们想要找到IV的大小和箱子个数的平衡点, 所以我们会对特征进行分箱, 然后计算每个特征在每个箱子数目下的WOE值, 利用IV值的曲线, 找出合适的分箱个数
-
逻辑回归的参数列表
| penalty | 可以输入"L1"或"L2"来指定使用那一种正则化方式, 不填写默认是"L2" 注意, 若选择"L1"为正则化, 参数solver仅能够使用求解方式"liblinear"和"saga", 若使用"L2"正则化,参数solver中所有的求解 方式都可用 |
| dual | 布尔值, 默认是False 使用对偶或原始计算方式, 对偶方式旨在求解器"liblinear"与L2正则项连用的情况下有效, 如果样本量大于特征数目, 这个参数设置为False回更好 |
| tol | 浮点数, 默认是1.00E-04 让迭代停下来的最小值, 数字越大, 迭代越早停下来 |
| C |
C正则化强度的倒数, 必须是一个大于0的浮点数, 不填写默认是1.0, 即默认正则项与损失函数的比值是1:1 C越小, 损失函数会越小, 模型对损失函数的惩罚越重, 正则化的效力越强, 参数θ会逐渐被压缩得越来越小 |
| fit_intercept |
布尔值, 默认是True 指定是否应将常量(比如说: 偏差,或截距)添加到决策函数中 |
| intercept_scalling |
浮点数, 默认是1 仅在使用求解器中"liblinear"且self.intercept设置为True时有用, 在这种情况下, x变为[x,self,intercept_scalling], 即具有等于intercept_scalling的常数值 的合成特征会附加到实际矢量中, 截距会变为intercept_scalling*syntheic_feature_weight |
| class_weight |
字典, 字典的列表, "balanced"或者None, 默认None 与标签相关联的权重, 表现方式是(标签的值: 权重)如果为None, 则默认所有的标签持有相同的权重, 对于多输出问题, 字典中权重的顺序需要与各个y在标签数据集 中的排列顺序相同 注意: 对于多输出问题(包括多标签), 定义的权重必须具体到每个标签的每个类, 其中类是字典键值对中的键, 权重是键值对中的值, 比如说, 对于四个标签, 且每个标签是 二分类(0和1)的分类问题而言, 权重应该被表示为: [{0:1, 1:1}, {0:1,1:5}, {0:1,1:1}, {0:1, 1:1}], 而不是 [{1:1}, {2:5}, {3:1}, {4:1}] 如果使用"balanced"模式, 将会使用y的值自动调整与输入数据中的类频率成反比的权重, 比如: n_samples/(n_classes*np.bincount(y)) *balanced_subsample模式与*balanced相同, 只是基于每个生长的树的随机放回抽样样本计算权重 注意: 如果指定了sample_weight, 这些权重将通过fit接口与sample_weight相乘 |
| random_state |
整数, sklearn中设定好的RandomState实例, 或None, 默认是None 当求解器是"sag"或, liblinear时才有效 1>输入整数, random_state是由随机数生成的随机数种子 2>输入RandomState实例, 则random_state是一个随机数生成器 3>输入None, 随机数生成器会是np.random模块中的一个RandomState实例 |
| solver |
字符, 可输入["newton-cg", "lbfgs", "liblinear", "sag","saga"], 默认"liblinear", 用于求解模型最优画的参数的算法, 即最优化问题的算法, 对于小数据集, liblinear 是一个不错的选择, 而"sag"和"saga"对于大数据集来说更快, 对于多分类问题, 只有"newton-cg", "sag","saga"和"lbfgs"能够处理多分类的损失函数, "liblinear"仅限于 一对多(ovr)和普通二分类方案 "newton-cg", "lbfgs", "sag"只处理L2正则项, 而"liblinear"和"saga"可与L1,L2正则项都连用, 请注意: "sag"和"saga"快速收敛仅在量纲大致相同的数据上得到保证 可以使用sklearn.preprocessing中的缩放功能来预处理数据 |
| max_iter |
整数, 可输入["ovr", "multinomial", "auto"], 默认是"ovr" 表示模型要处理的分类问题的类型, 如果输入"ovr", 表示分类问题是二分类, 或使用"一对多"的格式来处理多分类问题, 如果输入"multinomial", 最小化的损失函数是拟合在整个概率分布上的多项式损失函数, 即使数据二分类数据, 当参数solver的值是"liblinear"是, multinomial不可用 如果输入"auto", 则表示会根据数据的分类情况, 和其他参数来确定模型要处理的分类问题的类型, 比如说, 如果是二分类, 或者solver的取值为"liblinear", auto会默认选择 "ovr", 反之, 则会选择"multinomial" |
| verbose | 整数, 默认是0, 对于liblinear和lbfgs求解器, 将verbose设置为任何整数可以表示需要的拟合详细程度 |
| warm_start |
布尔值, 默认是False 设置为True, 是有那个上一次的拟合结果, 否则, 重新实例化一个模型来训练 |
| n_jobs |
整数或者None, 默认是None 在multi_class="ovr"中平行计算类别时使用的cpu线程数, 无论是否指定了multi_class, 当求解器设置为"liblinear"时, 都会忽略此参数, 如果次参数在joblib.parallel_bakckend上下文中, 就表示-1, 否则表示1, -1表示是哦那个处理器的所有线程来进行计算 |
逻辑回归的属性列表:
| coef_ |
数组, 结构 (1,n_features)或(n_classess, n_features) |
决策函数,即逻辑回归的预测函数中, 特征对应的系数 当给定问题时二分类问题, coef_具有形状(1,逆_features).特别地, 当multi_class ="multinomial"时, coef_对应于结果1(True), 并且-coef_对应于结果0(False) |
| intercept_ | 数组, 结构(1,)或, (n_classes) |
逻辑回归的预测函数中的截距(或者偏差) 如果fit_intercept设置为False, 则这个属性返回0, 当给定问题时二分类问题时, intercept_具有形状(1,) 特别是, 当multi_class="multinomial"时, intercept_对应于结果1(True), -intercept_对应于结果0(class) |
|
n_iter |
数组, 结构(n_class)或(1,) |
所有分类的实际迭代次数, 如果时二分类或multinomial的问题, 则只返回1个元素, 对于liblinear求解器, 会给出所有类的最大迭代次数 注意: 如果scipy版本<=1.0.0, lbfgs求解器的迭代次数可能超过mac_iter, 这这种情况下, n_iter最多返回max_iter |
逻辑回归的接口列表
| 接口 | 输入 | 功能 | 返回 |
| decision_function | 测试集x |
预测样本的置信度分数, 眼本的置信度得分时该样本于超平面的有符号距离 |
每个样本(样本, 类别)组合的置信度分数, 在二分类的情况下,self.classes_[1]的置信度 得分大于0的部分将样本预测预测为此类 |
| fit | 训练集x | 使用特征矩阵x拟合模型 | 拟合好的模型本身 |
| predict | 测试集x | 预测所提供的测试集x中样本点到额标签 | 返回模型预测的测试样本的标签 |
| predict_log_proba | 测试集x | 预测所提供的此时几x中样本点归属于各个标签对数概率 | 返回测试集中每个样本点对一个的每个每个标签的对数概率 |
| predict_proba | 测试集x | 预测所提供的测试集x中样本点归属于各个标签的概率 |
返回测试集中每个样本点对应的标签的概率, 对于multi_class问题, 如果multi_class问题, 如果multi_class参数设置为"multinomial" 则使用softmax函数用于查找每个类的预测概率, 否则就使用一对多ovr的方法, 即使用罗奇函数计算每个类假设为正的概率, 并在所有类中正则化这些值 |
| score | 测试集x, 测试集y | 用给定测速数据和标签的平均准确度作为模型的评分标准 | 返回给定数据和标签的平均准确度, 分数越高越好, 在多标签分了中返回子集的精度, 这是一个非常严格的度量, 因为我们需要为每个样本正确预测标签 |
| set_params | 新参数组合 | 在建立好的模型上,重新设置此评估器的参数 | 用新的参数组合重新实例化和训练的模型 |
| get_params | 不需要输入任何对象 | 获取此评估器的参数 | 模型的参数 |
| densify | 不需要输入任何参数 | 将系数矩阵转换为密集矩阵 | 转换好的密集矩阵 |
| sparsify | 不需要输入任何对象 | 将系数矩阵转换为稀疏矩阵 | 转换好的稀疏矩阵 |
ROC曲线和AUC面积(bonus)
-
F, T, P, N分别代表的含义:
- 预测值为正例, 记为P(Positive)
- 预测值为反例, 记为N(Negative)
- 预测值与真实值相同, 记为T(True)
- 预测值与真实值相反, 记为F(False)
| 真实值 | 预测值 | |
| 正例 | 反例 | |
| 正例 | TP | FN |
| 反例 | FP | TN |
- TP: 预测类别为P(正例), 真实类别是P(正例)
- FP: 预测类别时P(正例), 真实类别是N(反例)
- FN: 预测类别为N(反例), 真实类别是P(正例)
- TN: 预测类别为N(反例), 真实类别是N(反例)
样本中真实正例类别总数: TP+FN, TPR即True Position Rate, TPR=TP/(TP+FN)
- 所有正例中, 预测正确的概率(召回率)
样本中真实反例类别总是: FP+TN, FPR即False Position Rate, FPR=FP/(FP+TN)
- 所有反例中, 预测错误的概率
所以最理想的分类器: TPR =1. FPR=0
ROC曲线:
- 模型效果评估: 准确率: Accuracy
- 准确率Accuracy就是所有预测正确的样本除以总样本, 通常来说越接近1越好
- Accuracy = (TP+FN)/(TP+FP+FN+TN)
- 捕捉少数类: 精确度Precision
- 精确度,又叫查准率, 表示所有被我们预测为少数类的样本中, 正例少数类所占的比例, 精确度是将多数类判错后所需付出成本的衡量
- Precision = TP/(TP+FP)
- 捕捉少数类: 召回率Recall
- 召回率, 有被称为敏感度, 真正率, 查重率,表示所有真实为1的样本中, 被我们预测正确的样本所占的比例, 召回率越高,代表我们尽量捕出了越多的少数类,召回率越低,代表我们没有捕捉出足够的少数类
- Recall = TP/(TP+FN)
- 捕捉少数类F1_score,
- 为了同时兼顾精确度和召回率我们创造了两者的调和平均数走位考量两者平衡的综合性能指标F1_measure,两个数之间的调和平均倾向于靠近两个数中比较小的那个数, 因此我们追求尽量高的F1_measure, 能够保证我们的精确度和召回率都比较高,F_measure在[0,1]之间分布,越接近1越好
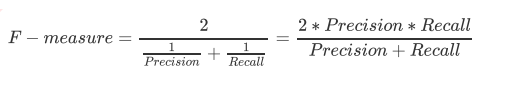
- 判错多数类:特异度Specificity
- 特异度表示所有真实为0的样本中,被正确预测为0的样本所占的比例
- Specificity = TN/(TN+FP)
- 还有一个概念叫”截断点”。机器学习算法对test样本进行预测后,可以输出各test样本对某个类别的相似度概率。比如t1是P类别的概率为0.3,一般我们认为概率低于0.5,t1就属于类别N。这里的0.5,就是”截断点”。
- ROC曲线:就是在不同的阈值下(截断点)下, 以FPR为横坐标, 找hi吕为纵坐标的曲线