参考博客:https://blog.csdn.net/weixin_43450885/article/details/105296033
https://www.zhihu.com/question/54504471
1.引言
传统的CNN由于具有平移不变性(即每个节点的邻居结点数都是固定的),经过训练可以很好的提取一些高层次的语义信息,但是对于一些社交网络,脑连接这些高维不规则型网格数据CNN并不能很好的工作,或者说没有办法去工作。文章考虑这种情况,扩展了CNN在更一般域上信号的可能推广,提出了空间域和频域上卷积操作的推广算法。一种是基于域的层次聚类(空间域),一种是基于图的拉普拉斯谱(频域,较为复杂,不是太懂)。最后对minst数据集进行测试,baseline为knn。
2.传统CNN
在传统的欧式空间中(以图像为例),在卷积时需要设置一定大小的步长,如stride = (3,3),假设input_image.shape = (18,18),kernel = (3,3),out_image.shape = (6,6),这个操作相当于在18×18个像素点中找到了6×6个聚类中心,将其进行聚类操作,每个类中的元素为中心点的邻域元素。将每个类与卷积核对应项相乘求和,得到输出的一个像素点。这是传统的卷积操作,可以看作一个聚类的操作。
传统的卷积操作相比于一般的线性映射有权重共享等优势,其次还有多尺度二进聚类允许子采样,即分层次表达信息并综合考量;再者也支持紧密连接的滤波器可以自动提取图像特征。
3.改良的卷积操作--深度局部连接网络(空间域上的改良)
3.1邻域的概念
在传统的欧式空间中(以图像为例),在卷积时需要设置一定大小的卷积核,如 kernel = (3,3),就是相当于中心像素点的邻域为周围的8个像素点。
在图中,利用WWW来确定每个节点的邻域。论文中给出公式: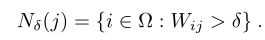
表示以δ为阈值,大于它的才是j结点的邻域
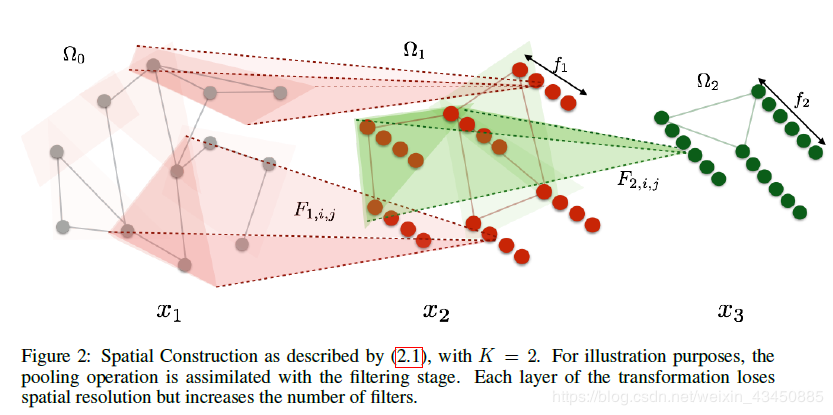
3.2深度局部连接网络构造原理--(空间域)

上述公式中,k表示第k个尺度,可以理解为第k个卷积层,定义Ωk表示第k层的输入节点数目,dk-1表示第k-1层的聚类类数,即第k层的输入数目,即Ωk=dk-1
每层输出的Xk公式如下:

其中,fk-1表示k-1层的滤波器个数,也是k层中每个节点的特征维数。Xk表示输入数据,他的大小跟上一层的输出数据相同,上一层的输出数据与该层聚类类数和滤波器个数有关,所以,Xk的shape为(dk-1,fk-1)。Fk,i j表示第k层第j个滤波器的第i个值,若x和y节点不是邻域关系,Fk,i j(x,y)的值为0.
上述意思是h为非线性激励函数,L为池化操作,h括号中的相当于卷积操作。

4.频域意义上的卷积操作结果公式分析
4.1公式推导过程---(我也不清楚。。)


对于上述推导我并不是太明白,但我们只需明白公式11的含义及其表达意义即可
在公式(11)中,等式表示由Xk,i经过一系列变换为Xk+1,j,其中Xk,i可以理解为输入信号,由傅里叶和拉普拉斯定义的卷积操作对每个输入信号进行卷积操作后进行累加,得出一个值,该值可以理解为Feature maps,由扩展卷积操作后提取的Feature maps,Xk,i的具体含义是第K层上所有结点的第i个特征拼接形成的向量,Fk,i,j可以理解为滤波器,VT起到一个发现到底有没有相邻节点的作用。最后做一个非线性映射激活。
5.小结
该论文提出了一种处理非结构数据的方法,最大程度保留CNN在提取特征时的好处和优点,将其运用在非结构数据提取特征的渠道上,并具有较强的可解释性。论文的其他部分类似于一些优化操作的部分,我觉得这种思想是最重要的,所以后续可能会更新些其他小的部分。自己太菜了。。。。。呜呜呜
最后附一个GitHub的该文章代码实现(转):
https://github.com/Ivan0131/gcn_demo/blob/master/graph_convolution_network.ipynb
6.补充
直观理解图卷积网络-----------https://mp.weixin.qq.com/s/sg9O761F0KHAmCPOfMW_kQ
数学角度理解图卷积网络-----https://blog.csdn.net/lijunweiyhn/article/details/87926425