决策树算法之C5.0

C5.0是对ID3算法的改进。

　1.引入了分支度Information Value的概念。

　　

 　　　　C5.0是用哪个信息增益率作为判断优先划分属性的。

　　　　信息增益率其实就是在信息增益   除了 分支度。分支度的计算公式如上，就是指，若某划分属性S将样本T划分成n个子集T1,T2,...Tn，则此属性S的分支度就等于：每个分支子集Ti的个数ci， 出于样本总个数t，然后再乘以log₂ci/t，然后再把各个分支的计算值加起来。

　　   

 2. C5.0和C4.5可以处理数值型数据，处理方式如下图：

　　

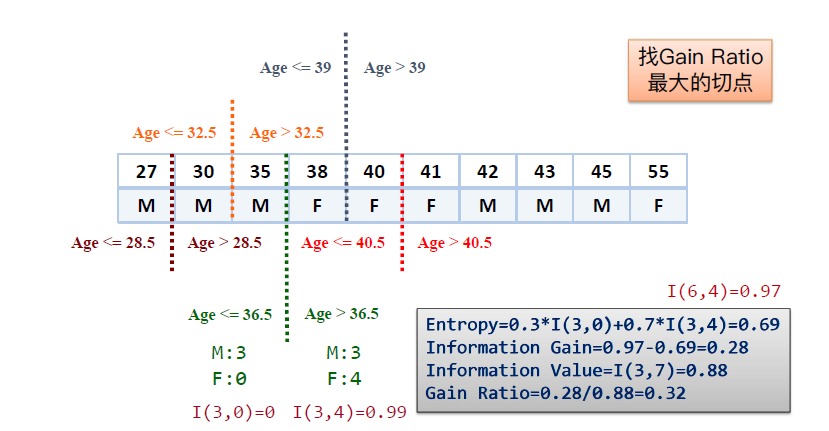
　　核心思想：将数值从小到大排序，对每两个数值间进行试探切割，算出Gain Ratio，找到最大的那个切割Gain Ratio，进行切割离散化。

3.剪枝

　　C4.5和C5，要对决策树进行剪枝，剪枝的目的是为了避免过拟合问题。

　　这两种算法的剪枝方法是Bottom-Up从下往上剪枝，也就是说，先利用训练集把决策树建好。然后从下往上砍树。

　　剪枝方法：

　　　　对于每一个分支b1,b2,b3等，根据b1里面的数据数量S(b1)，以及里面的Y的数量6，和N数量0，利用一个很复杂的统计学公式可以计算出该节点的“预期错误率U_25%（6,0）”

　　　　每个分支的预期错误值Ei = 分支里面的总个数S(bi)*U_25%，最后将所有的分支b1,b2,b3...的错误值加起来，就得到错误值之和Eb。

　　　　

　　　　再然后，假如，b1,b2,b3三个分支的总的Y的数量假如为15Y,总的N的数量为1N。如果将B子树砍掉，则在a1分支之后就有 15Y,1N，同样可以计算此a1节点，不做往下分支的错误值为：Ea1 = 16*U_25%

　　　　剪枝的判断依据：如果Ea1>Eb，不剪枝；如果Ea1<Eb，剪枝。

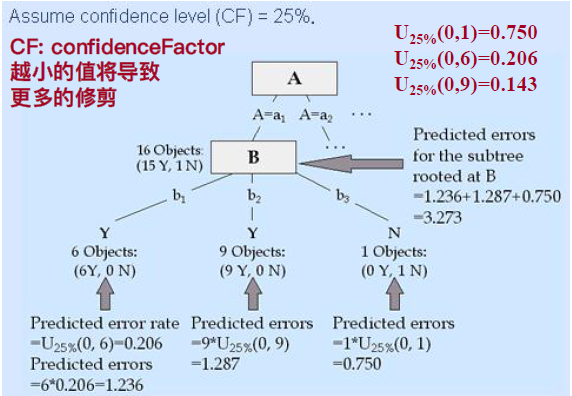
 　　　　　　　　（图片来自：经管之家CDA）