决策树算法之ID3

ID3算法

　　ID3使用信息增益（information Gain）作为属性选择方法。信息增益基于信息论中熵（Entropy）的概念。熵是衡量一个节点不纯度的指标。

　　熵越大，节点越不纯，当熵=0时，节点最纯。

　　　　假设一个训练样本集T是含有t个数据的样本集合，假设T在类属性C上有n个不同的值，且在类属性C上的n个值相同的记录被划分为一类，则样本集T被划分成为n个类{C1,C2,C3,...Cn}。ci表示Ci类的个数。对于这个给定的样本集T，它的熵被定义为：

　　

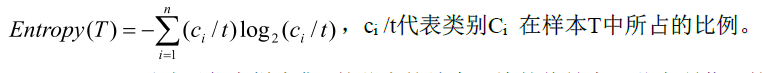
     第一步，先计算出目标分类属性的熵值Entropy(T)。

 　第二步，再计算出，按照某划分属性S将T划分为m个子集{T1,T2,T3,...Tm}，其中Tj中的记录为S上有相同的值Sj。设Tj的数据个数为tj。则用S属性来划分T的熵定义为：

　　

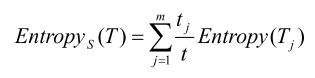
　　Entropys(T)反映了用属性S来划分T所需要的信息量。

　　属性S的信息增益 等于： 

　　　　　　

　　信息增益是用来衡量由于划分造成的Entropy减小的程度，也就是属性S对样本T的贡献。Entropy减小的程度越大，则根据该属性S产生的划分就越纯，信息增益的值Gain就越大。因此，选择信息增益最大的属性最为划分属性。

　　举例如下：

　　

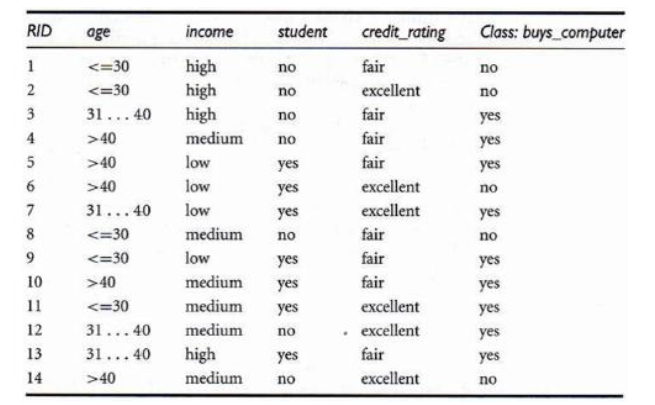
　　我们先对目标分类属性：是否买电脑计算熵值：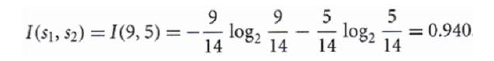

 　　第二步，我们选一个属性“年龄（age）”作为入手，按照年龄可以将T划分成3个子集T1:{age<=30}；T2{40>=age>30}；T3{age>40}

　　

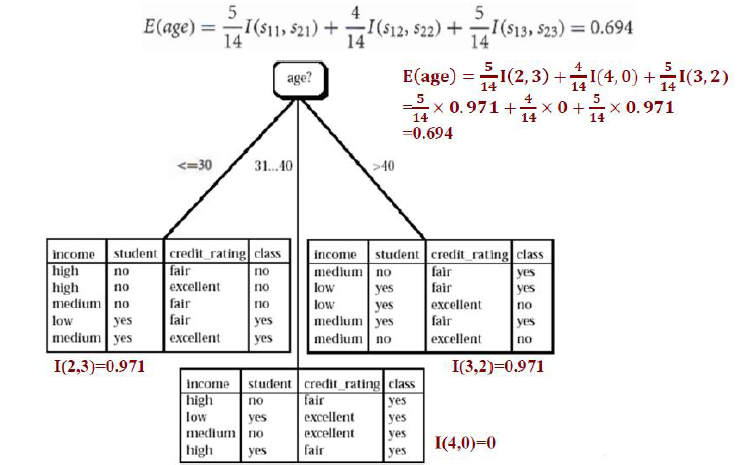
　　我们按照熵的计算公式，分别计算这三个子集的熵值:

　　　　I1(2,3)=-2/5*log₂(2/5)-3/5*log₂(3/5)=0.971

　　　　I1(4,0)=-4/4*log₂(4/4)-0/4*log₂(0/4=0

　　　　I1(3,1)=-3/5*log₂(3/5)-2/5*log₂(2/5)=0.971

      因此，E(age) = 5/14*I1(2,3)+4/14*I2(4,0)+5/14*I3(3,2) = 0.694。

　　所以信息增益Gain(age) =E(T)-E(age)=0.940-0.694=0.246。

　　同理，把其他的属性也以同样的方式计算出各自的信息增益Gain(Studeng)，Gain(credit_rating)，。。。看看那个信息增益最大，就把此属性作为第一分类属性。