Surround the Trees
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 9703 Accepted Submission(s): 3725
Problem Description
There
are a lot of trees in an area. A peasant wants to buy a rope to
surround all these trees. So at first he must know the minimal required
length of the rope. However, he does not know how to calculate it. Can
you help him?
The diameter and length of the trees are omitted, which means a tree can be seen as a point. The thickness of the rope is also omitted which means a rope can be seen as a line.
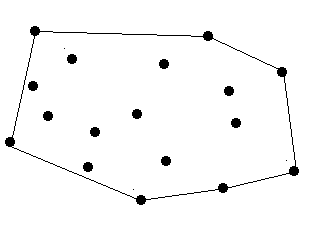
There are no more than 100 trees.
The diameter and length of the trees are omitted, which means a tree can be seen as a point. The thickness of the rope is also omitted which means a rope can be seen as a line.

There are no more than 100 trees.
Input
The
input contains one or more data sets. At first line of each input data
set is number of trees in this data set, it is followed by series of
coordinates of the trees. Each coordinate is a positive integer pair,
and each integer is less than 32767. Each pair is separated by blank.
Zero at line for number of trees terminates the input for your program.
Zero at line for number of trees terminates the input for your program.
Output
The minimal length of the rope. The precision should be 10^-2.
Sample Input
9
12 7
24 9
30 5
41 9
80 7
50 87
22 9
45 1
50 7
0
Sample Output
243.06
凸包,1,2的时候记得讨论。。。
///题意:国王要在城堡外修一个外墙,这一个外墙要隔城堡至少m英尺,求修这个外墙需要的最小费用 ///分析:我们先要找到刚好囊括整个城堡的一个外墙,这里要利用凸包算法,然后加上一个圆的周长 /** 令p0为Q中Y-X坐标排序下最小的点 设<p1,p2,...pm>为对其余点按以p0为中心的极角逆时针排序所得的点集(如果有多个点有相同的极角,除了距p0最远的点外全部移除 压p0进栈S 压p1进栈S 压p2进栈S for i ← 3 to m do while 由S的栈顶元素的下一个元素、S的栈顶元素以及pi构成的折线段不拐向左侧 对S弹栈 压pi进栈S return S; */ #include<stdio.h> #include<iostream> #include<string.h> #include<math.h> #include<algorithm> using namespace std; const int N = 105; const double pi = atan(1.0)*4; const double eps = 1e-8; struct Point { double x,y; } p[N]; Point Stack[N]; ///模拟栈,不然的话取到栈的第二个元素不好处理 int n; double mult(Point a,Point b,Point c){ return (a.x-c.x)*(b.y-c.y)-(a.y-c.y)*(b.x-c.x); } double dis(Point a,Point b){ return (a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y); } int cmp(Point a,Point b){ if(mult(a,b,p[0])>0) return 1; if(mult(a,b,p[0])==0&&dis(b,p[0])-dis(a,p[0])>eps) return 1; return 0; } int Graham(){ int top = 2; sort(p+1,p+n,cmp); Stack[0] = p[0]; Stack[1] = p[1]; Stack[2] = p[2]; for(int i=3;i<n;i++){ while(top>=1&&mult(p[i],Stack[top],Stack[top-1])>=0) top--; Stack[++top]=p[i]; } return top; } int main() { while(scanf("%d",&n)!=EOF&&n) { for(int i=0; i<n; i++) { scanf("%lf%lf",&p[i].x,&p[i].y); } if(n==1) { printf("0.00 "); continue; } if(n==2){ printf("%.2lf ",sqrt(dis(p[0],p[1]))); continue; } int k=0; for(int i=0; i<n; i++) { if(p[i].y<p[k].y||((p[i].y==p[k].y)&&(p[i].x<p[k].x))) k = i; } swap(p[0],p[k]); double sum=0; //printf("%lf %lf",p[0].x,p[0].y); int top = Graham(); for(int i=1;i<=top;i++){ sum+=sqrt(dis(Stack[i],Stack[i-1])); } sum+=sqrt(dis(Stack[0],Stack[top])); printf("%.2lf ",sum); } return 0; }