关于最小生成树,网上有很多的资料,就不写这么多了~非常推荐 啊哈算法的讲解,这本书对最短路,最小生成树,都讲得非常棒~
一:定义:
一个有 n 个结点的连通图的生成树是原图的极小连通子图,且包含原图中的所有 n 个结点,并且有保持图连通的最少的边。
简单来讲,就是搜索到的边子集所构成的树中,不但包括了连通图里的所有顶点,且其所有边的权值之和为最小。
二:算法实现:
1:Kruskal算法
加边法,先依据边权进行排序。
从小到大遍历,如果两个点不在同一个集合内,则加入生成树。而判断集合使用了并查集。
n个顶点的图连通,至少需要n-1条边。所以可以依据此,来判断最小生成树是否存在。
板子:

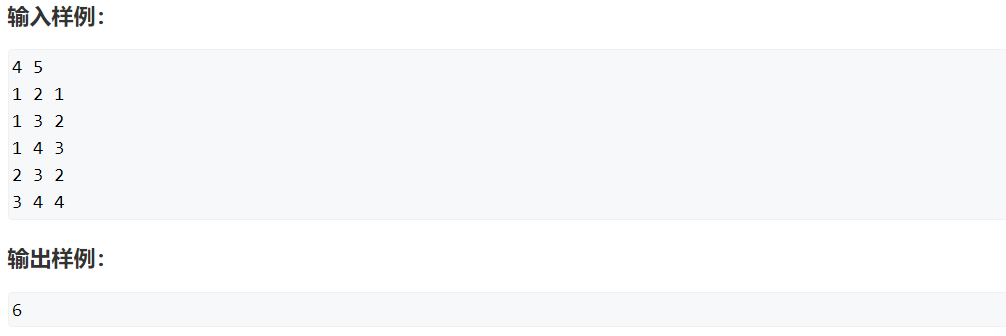
时间复杂度:MlogM
#include<iostream> #include<cstring> #include<algorithm> #include<queue> #include<map> #include<stack> using namespace std; typedef long long ll; const int maxn=2e5+10; const int inf=99999999; int n,m; int pr[maxn]; struct node { int a,b,c; }st[maxn]; bool cmp(node a,node b) { return a.c<b.c; } int find(int x) { if(x!=pr[x]) return pr[x]=find(pr[x]); return x; } bool check(int a,int b) { int f1=find(a),f2=find(b); if(f1!=f2) { pr[f1]=f2; return true; } return false; } int main() { cin>>n>>m; for(int i=1;i<=n;i++) pr[i]=i; for(int i=1;i<=m;i++) { cin>>st[i].a>>st[i].b>>st[i].c; } sort(st+1,st+1+m,cmp);//按权值从小到大 int minn=inf; int sum=0; int cnt=0; for(int i=1;i<=m;i++) { if(check(st[i].a,st[i].b))//如果不在同一个集合,就连一起 { sum+=st[i].c; cnt++; } if(cnt==n-1) break; } if(cnt<n-1) cout<<"impossible"<<endl; else cout<<sum<<endl; }
2:Prim算法
随便选一个点开始来生成最小生成树,因为n个顶点都要得到。
与dijkstra类似,但是dis[]数组并不是表示1号点到各个点的最短距离,而是未构成树的点,离树的最短距离。即如果dis[k]>e[j][k],就更新dis[k]
板子:
#include<iostream> #include<cstring> #include<algorithm> #include<queue> #include<stack> using namespace std; const int maxn=5e2+10; const int inf=0x3f3f3f3f; int e[maxn][maxn],vis[maxn],dis[maxn]; int n,m; int prim() { int cnt=1,sum=0;//sum记录答案,cnt记录加入树的点数 vis[1]=1; while(cnt<n) { int minn=inf; int idx=-1; for(int i=1;i<=n;i++) { if(!vis[i]&&dis[i]<minn) { minn=dis[i]; idx=i; } } if(idx==-1) return inf;//cnt<n,未完成构建,但是没有新点加入,则无解 vis[idx]=1;//已加入 sum+=dis[idx]; cnt++; for(int i=1;i<=n;i++) { if(!vis[i]&&dis[i]>e[idx][i]) dis[i]=e[idx][i];//更新 i 号点到树的距离 } } return sum; } int main() { cin>>n>>m; for(int i=1;i<=n;i++) { for(int j=1;j<=n;j++) { if(i==j) e[i][j]=0; else e[i][j]=inf; } } for(int i=1;i<=m;i++) { int a,b,c; cin>>a>>b>>c; e[a][b]=min(e[a][b],c); e[b][a]=min(e[b][a],c); } for(int i=1;i<=n;i++) dis[i]=e[1][i]; //以1号点为起点 int t=prim(); if(t==inf) puts("impossible"); else cout<<t<<endl; }