地址:https://www.acwing.com/problem/content/855/
解析:
图里含有负权边,所以考虑Bellman_ford算法。
Bellman_ford就是从局部扩展到全局,得的是局部最优解,与Dijkstra有着很大不同。
本题要求最多经过k条边到n点的最短距离,那么引入back[]数组,用来记录上一次dis[]的状态。
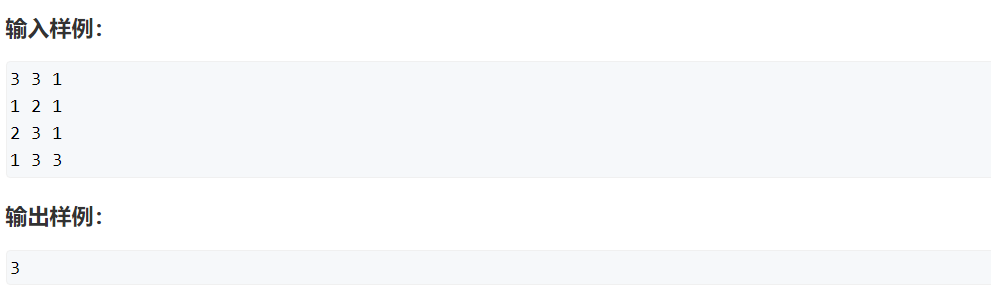
对于样例一:在第一次的Bellman_ford中,2->3是不应该被更新的,只能更新1->3,这里就体现了back[]数组的作用。具体的建议手推几遍。
#include<iostream> #include<cstring> #include<algorithm> #include<queue> #include<stack> using namespace std; const int maxn=1e4+10; const int inf=0x3f3f3f3f; int u[maxn],v[maxn],w[maxn]; int dis[maxn],back[maxn]; int n,k,m; int bellman_ford() { memset(dis,inf,sizeof(dis)); dis[1]=0; for(int i=1;i<=k;i++) { memcpy(back,dis,sizeof(dis)); for(int i=1;i<=m;i++) { dis[v[i]]=min(dis[v[i]],back[u[i]]+w[i]); } } if(dis[n]>inf/2) return -1; return dis[n]; } int main() { cin>>n>>m>>k; for(int i=1;i<=m;i++) { cin>>u[i]>>v[i]>>w[i]; } int t=bellman_ford(); if(t==-1) cout<<"impossible"<<endl; else cout<<t<<endl; }