地址:https://www.acwing.com/problem/content/156/
这题和POJ2823是一样的
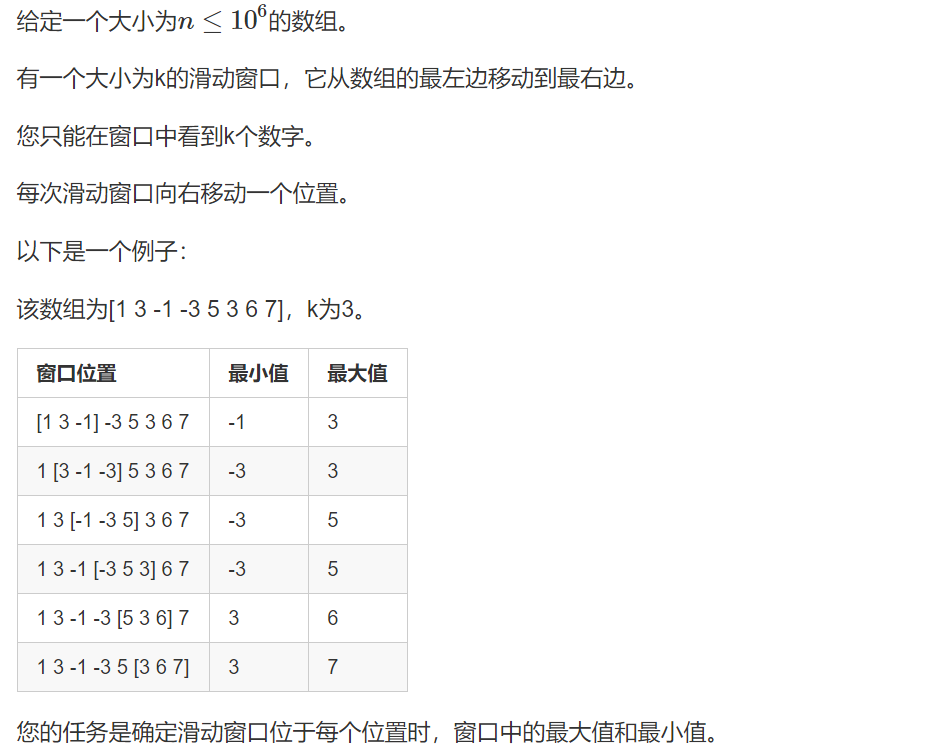
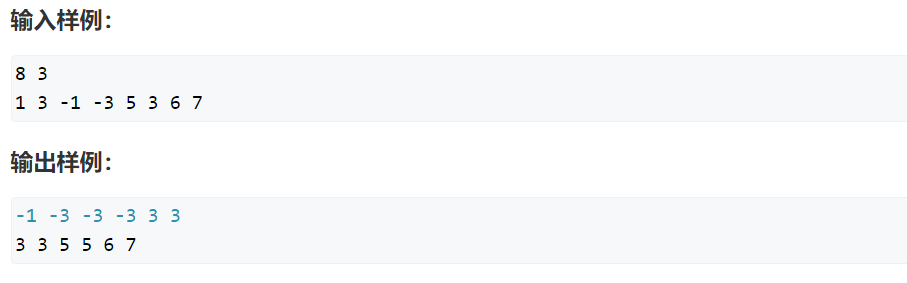
解析:
暴力,直接对于每k个都遍历一遍,很显然复杂度O(nk)的话行不通。
对于这类问题,有一个比较一致的思路,就是有些数字是无用的,或者用了几次后就要被扔掉的,后续根本就排不上用场。
比如有ai,aj,ax,ax>ai>aj,找ax左边第一个比它小的数,很明显,ai压根不需要看,因为在ai之后有更小的aj
所以这就是单调队列,队列里存储的是单调递增或递减的数字。
单调队列与单调栈的区别之一就是,单调队列维护两端,它的头端可以出数,尾部可以进数。这个题的滑动窗口,队列里存下标,下标超范围的话是需要出队列的,而进队列是从队列尾插入。
先维护一遍最小,然后最大,代码基本一致,单调性不同。
单调队列的时间复杂度为O(n)
#include<cstdio> #include<cstring> #include<vector> #include<set> #include<algorithm> #include<iostream> #include<vector> using namespace std; typedef long long ll; const int maxn=1e6+10,maxn2=31*maxn; int a[maxn],q[maxn];//¶ÓÁÐÀï´æϱê int n,k; int main() { scanf("%d%d",&n,&k); int hh=0,tt=-1; for(int i=0;i<n;i++) scanf("%d",&a[i]); for(int i=0;i<n;i++) { if(hh<=tt&&i-k+1>q[hh]) hh++; while(hh<=tt&&a[i]<=a[q[tt]]) tt--; q[++tt]=i; if(i>=k-1) cout<<a[q[hh]]<<" "; } hh=0,tt=-1; cout<<endl; for(int i=0;i<n;i++) { if(hh<=tt&&i-k+1>q[hh]) hh++; while(hh<=tt&&a[i]>=a[q[tt]]) tt--; q[++tt]=i; if(i>=k-1) cout<<a[q[hh]]<<" "; } }