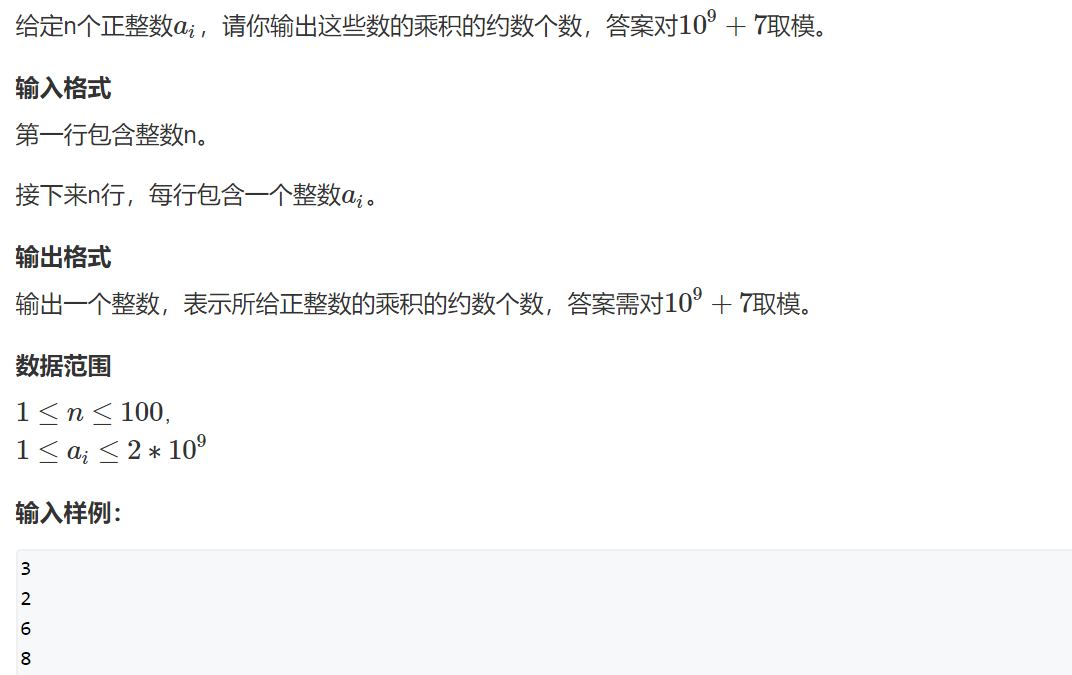
地址:https://www.acwing.com/problem/content/872/
课程没买的话,应该是看不了的,所以截个图。

唯一分解定理:

则N的约数个数就为:
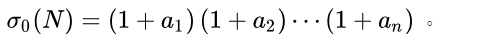
证明:P1^a1的约数个数为a1+1
P2^a2的约数个数为a2+1
.....
根据乘法原理,即为:
(1+a1)*(1+a2)....(1+an)
所以,把每一个乘数拆开来,求出它们的a1,a2....存在map里,最后的时候,套约数个数公式即可。
#include <bits/stdc++.h> using namespace std; typedef long long ll; const int maxn=1e5+50; const int mod=1000000007; const int inf=1e9; int main() { map<int,int>mp; int n; cin>>n; while(n--) { ll x; cin>>x; for(int i=2;i<=x/i;i++) { if(x%i==0) { while(x%i==0) { mp[i]++; x=x/i; } } } if(x>1) mp[x]++; } ll sum=1; for(map<int,int>::iterator it=mp.begin();it!=mp.end();it++)//!!!!!!!!!!!!!!! { sum=sum*(it->second+1)%mod; } cout<<sum<<endl; }
约数求和:
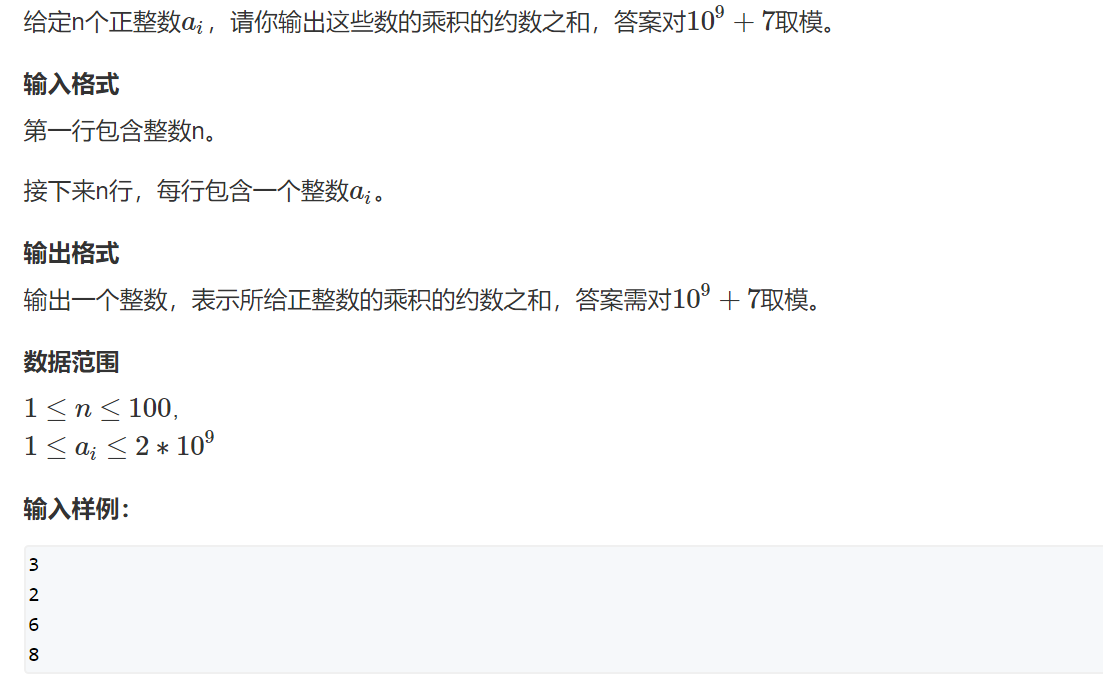

计算公式:
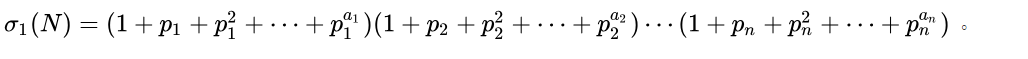
#include <bits/stdc++.h> using namespace std; typedef long long ll; const int maxn=1e5+50; const int mod=1e9+7; const int inf=1e9; int main() { map<int,int>mp; int n; cin>>n; while(n--) { ll x; cin>>x; for(int i=2;i<=x/i;i++) { if(x%i==0) { while(x%i==0) { mp[i]++; x=x/i; } } } if(x>1) mp[x]++; } ll sum=1; for(map<int,int>::iterator it=mp.begin();it!=mp.end();it++) { int p=it->first,a=it->second; ll md=1; ll kk=1; while(a--) { kk*=p; kk%=mod; md+=kk; md=md%mod; } sum=(sum*md)%mod; } cout<<sum<<endl; }