牛客小白月赛24 J-建设道路(注意负数取模)

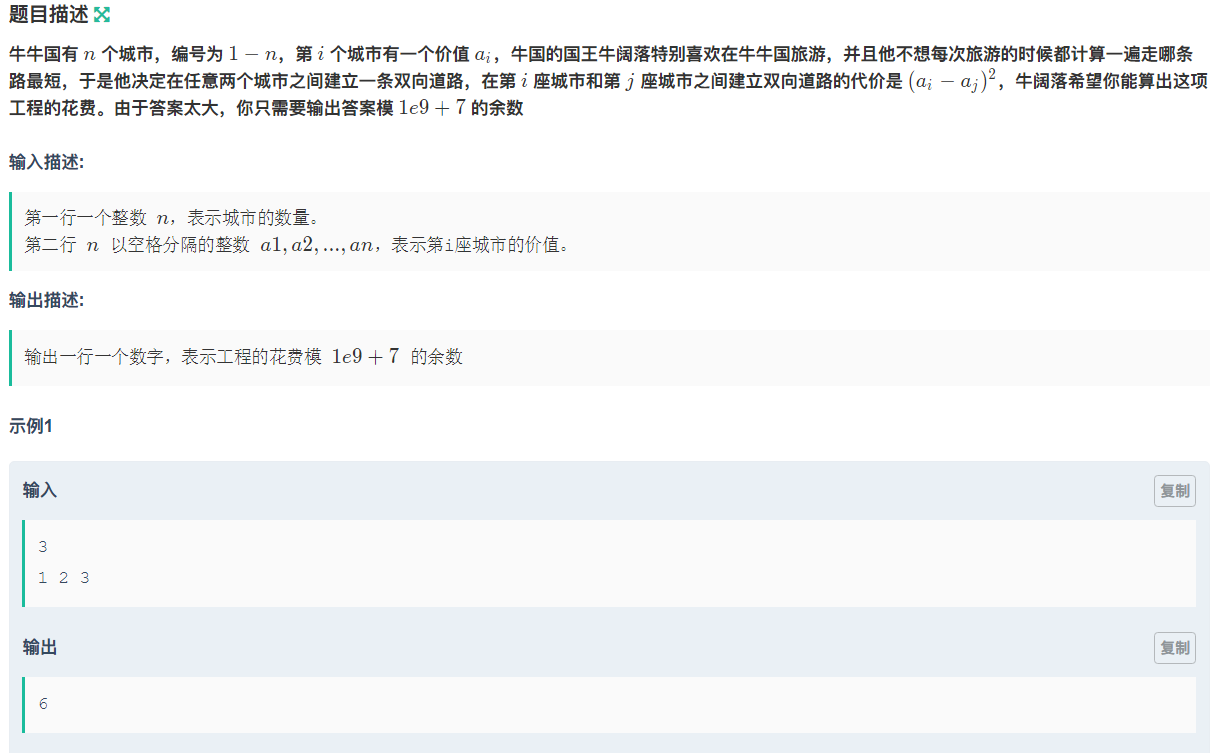
 　　　　解析：把这个式子展开，就是a^2-2ab+b^2。对于每个数的平方，都出现了n-1次。所以把每个数的平方加起来，乘(n-1)就可以了。对于2ab的部分，举个例子：

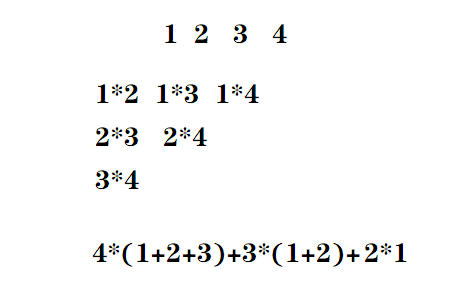
 　　　　      　 可以看出，是每个数乘上它之前的前缀和。所以答案就是"平方和*(n-1)-从第二个数往后每个数*(它之前的前缀和)*2"。注意取模，保证取模后的结果为正数，我们的花费不可能是负数：(x%mod+mod)%mod。

#include<iostream>
#include<vector>
#include<algorithm>
#include<set>
#include<map>
#include<cmath>
using namespace std;
typedef long long ll;
const ll mod=1e9+7;
const int maxn=5e5+10;
ll a[maxn];
ll q[maxn];
int main()
{
    int n;
    scanf("%d",&n);
    ll sum1=0,sum2=0;
    q[0]=0;
    for(int i = 1 ;i <= n  ; i++)
    {
        scanf("%lld",&a[i]);
        sum1=(sum1+(a[i]*a[i])%mod)%mod;
        q[i]=(a[i]+q[i-1])%mod;
    }
    for(int i=2;i<=n;i++)
    {
        sum2=(sum2+a[i]*q[i-1]%mod)%mod;
    }
    cout<<(sum1*(n-1)%mod-sum2*2%mod+mod)%mod<<endl;
}