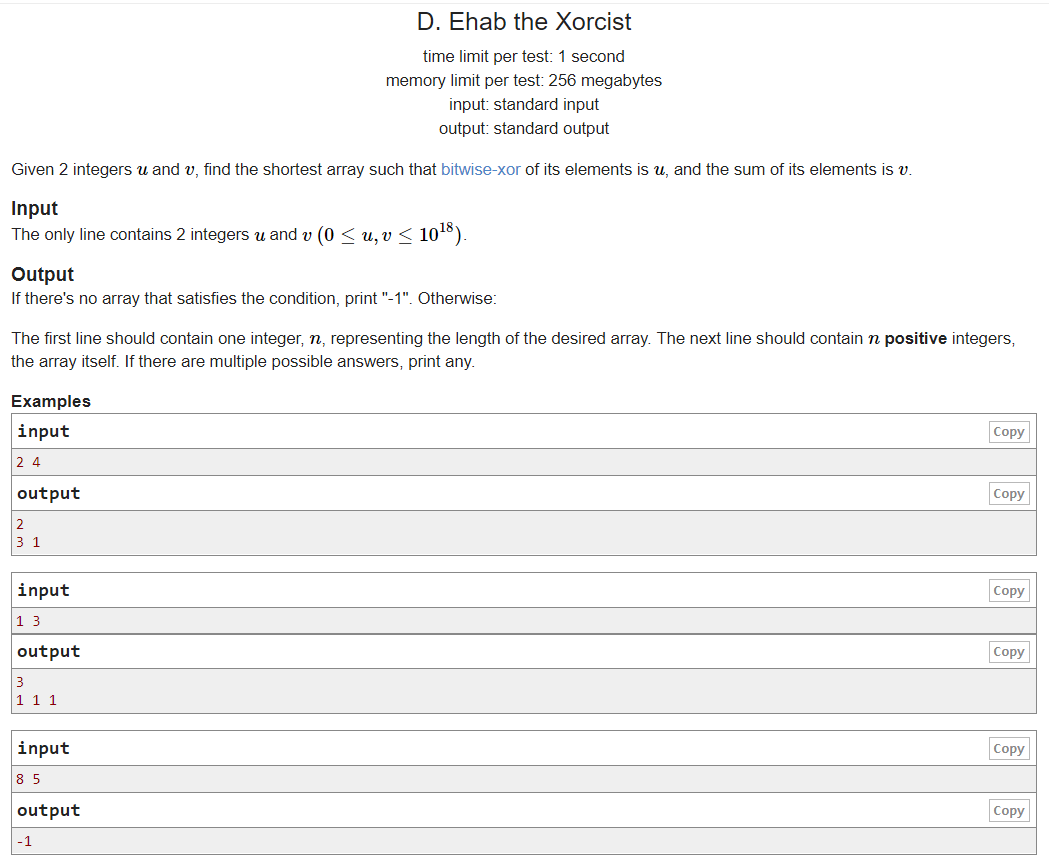
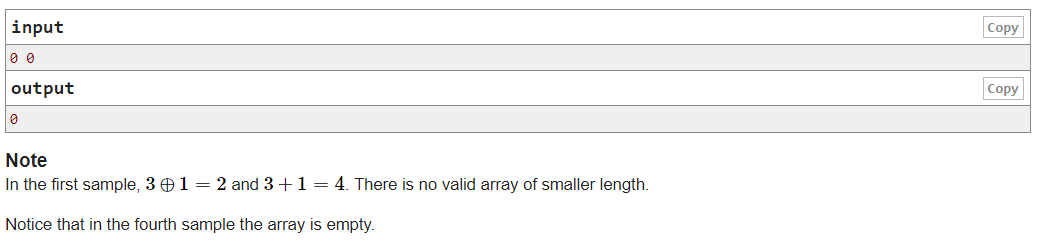
题意:给出u,v。要求给出一个最短的数组,要求这个数组异或结果为u,和为v。
解析 :所谓xor,相同为0,否则为1。就是一个不进位的二进制加法(这里不理解的建议去看看二进制加法法则,再与此做对比)。
1:u>v。根据上述,不进位的u都比v大,那进位的话会更大,这些数加起来肯定比v大,所以无解,-1。
2:u==v,直接输出u即可
3:u<v。我们可以从结果为3个 数入手。可以构造为x,x,u。为什么,因为x^x==0,而0异或一个数等于这个数的本身,即x^x^u==u。要想保证和为v,那么x=(v-u)/2即可。这个要保证整除,所以(v-u)%2!=0肯定无解了。看样例,存在结果有2个的情况,这里实际上是进行了合并。有两种合并方式:2x,u和x,x+u。2x,u是不可以的。如果2x^u==u,那么2x==0,于是2x+u==v==u,这不符合u<v的前提。所以x,x+u为正确合并方式,已知x=(v-u)/2,那么x+u就为(v+u)/2,那么我们直接算出mid1=(u+v)/2,mid2=(v-u)/2,判断是否满足mid1+mid2==v而且mid1^mid2==u即可。先判断它,因为题目要求最短数组。不行的话,再输出3个的情况。
#include<iostream> #include<cstdio> #include<cstring> #include<queue> using namespace std; typedef long long ll; //priority_queue<ll,vector<ll>,greater<ll> >q; int main() { ll u,v; cin>>u>>v; if(u==0&&v==0) { cout<<"0"<<endl;return 0; } if(u>v) cout<<"-1"<<endl; else if(u==v) { cout<<"1"<<endl; cout<<u<<endl; } else { ll mid1=(u+v)/2; ll mid2=(v-u)/2; if((v-u)%2!=0) { cout<<"-1"<<endl;return 0; } if((mid1+mid2)==v&&(mid1^mid2)==u) { cout<<"2"<<endl; cout<<mid1<<" "<<mid2<<endl; return 0; } cout<<"3"<<endl; cout<<mid2<<" "<<mid2<<" "<<u<<endl; } }
还有一套解法:推荐看这个博主写的https://www.cnblogs.com/1024-xzx/p/12505710.html
插个公式: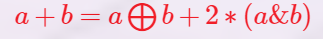
即加法=不进位加法+进位数字