A

For each prefix of a given string S with N characters (each character has an ASCII code between 97 and 126, inclusive), we want to know whether the prefix is a periodic string. That is, for each i (2 <= i <= N) we want to know the largest K > 1 (if there is one) such that the prefix of S with length i can be written as A ^K,that is A concatenated K times, for some string A. Of course, we also want to know the period K.

Input

The input consists of several test cases. Each test case consists of two lines. The first one contains N (2 <= N <= 1 000 000) – the size of the string S.The second line contains the string S. The input file ends with a line, having the 
number zero on it.

Output

For each test case, output "Test case #" and the consecutive test case number on a single line; then, for each prefix with length i that has a period K > 1, output the prefix size i and the period K separated by a single space; the prefix sizes must be in increasing order. Print a blank line after each test case.

Sample Input

3
aaa
12
aabaabaabaab
0

Sample Output

Test case #1
2 2
3 3

Test case #2
2 2
6 2
9 3
12 4
　　　　　　地址：　　hdu1358　　http://acm.hdu.edu.cn/showproblem.php?pid=1358
　　　　求最小循环节,比如样例2：　　　　aabaabaabaab
　　　　　　　　　　　　　　　　　　　　6  2    表示第6个为止，有两个循环节。不要有重叠。
　　　　再举例：　　　　

　　　　　　　　　　　　　　9
　　　　　　　　　　　　　　aabaabaab
　　　　　　　　　　　　　　Test case #1
　　　　　　　　　　　next:　-1 0 1 0 1 2 3 4 5 6
　　　　　　　　　　　　i:　　0 1 2 3 4 5 6 7 8 9

　　　　　　　　　　根据next数组，我们可以做：int    k =  i-next[i];　　k即为到第i的段的最小循环节。比如在i=7的位置，其next值为4。为什么是4？因为:

　　　　　　　　

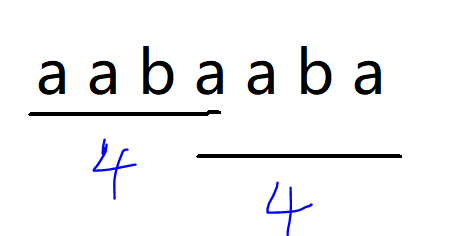
　　　　　　　　此有重叠部分。然后：

　　　　　　　　

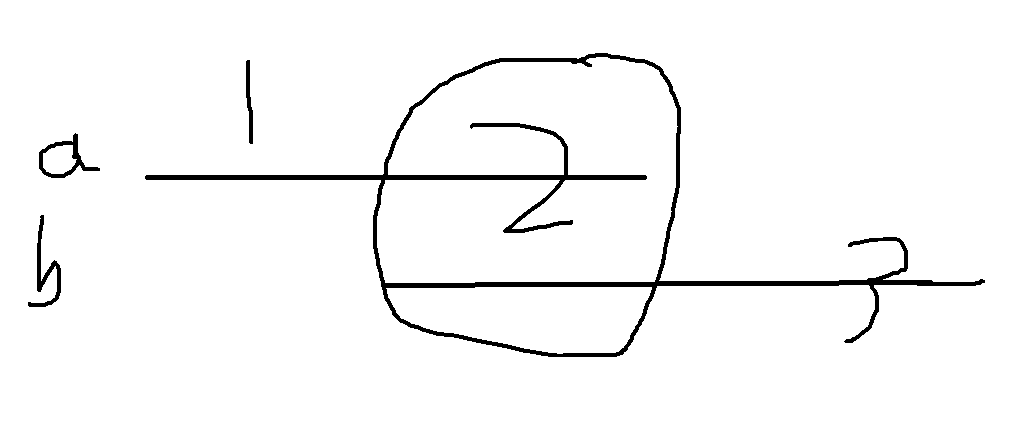
　　　　　　　　如果a与b相同，那么1处与2处必定相同。那么  i - next[i]变为1处长度，那么既然1==2，此就为**最小循环节**。如果像上两图中，俩循环节有重叠部分，明显不符合题意。因为 总长度%k!=0，会把3处余出来（这里是3！=2的情况，如果1==2==3的话，那就不是重叠的情况了。）。

　　　　　　　　像这种的：aaa  aaa .在i=6的时候，next=5,  6 - 5==1,   6%1==0,6 /1 =6 ,便为6个循环节。

　　　　　　　　又比如：aab aab aab  在i=9的时候，next=6,  9-6==3,  9%3==0，9/3=3，便为3个循环节。 

　　　　　　　　next==-1||==0的不符合题意，判断一下就好了。主要是对next数组的理解！！

　　　　　　

#include<iostream>
#include<cstring>
#include<map>
#include<set>
#include<cstdio>
using namespace std;
typedef long long ll;
const int maxn=1e6+10;
char a[maxn];
int next[maxn];  
void  pr(int n)
{
    next[0]=-1;
    int k=-1;
    int j=0;
    while(j<n)
    {    
        if(k==-1||a[j]==a[k])
        {
            ++k;
            ++j;
            next[j]=k;
        }
        else
            k=next[k];
    }
}  
int main()
{
    int n;
    int ac=1;
    while(cin>>n)
    {
        if(n==0)
            break;
        cin>>a;
        pr(n);
        printf("Test case #%d
",ac++);
//            for(int i=0;i<=n;i++)
//            cout<<next[i]<<" ";
        for(int i=1;i<=n;i++)
        {
            int k=i-next[i];
            if(next[i]==-1||next[i]==0)
                continue;
            if(i%k==0)
            {
                printf("%d %d
",i,i/k);
            }
        }    
        cout<<endl;
    }
}